《2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社》

【例 1】在 $ \triangle ABC $ 中，$ \angle C=90^{\circ} $。
(1) 已知 $ AC=6 $，$ BC=8 $。求 $ AB $ 的长为10；
(2) 已知 $ AB=17 $，$ AC=15 $，求 $ BC $ 的长为8。

答案： 【解析】：在直角三角形中，根据勾股定理，两直角边的平方和等于斜边的平方。对于（1），已知直角边$AC = 6$，$BC = 8$，求斜边$AB$，则$AB=\sqrt{AC^{2}+BC^{2}}$；对于（2），已知斜边$AB = 17$，直角边$AC = 15$，求另一直角边$BC$，则$BC=\sqrt{AB^{2}-AC^{2}}$。
【答案】：（1）$10$；（2）$8$

针对训练 1 已知一个直角三角形的两边分别为 3 和 4，则第三边的平方为 （D）
A. 25
B. 14
C. 7
D. 25 或 7

答案： D

【例 2】如图，水池中离岸边 $ D $ 点 1.5 米的 $ C $ 处，直立长着一根芦苇，出水部分 $ BC $ 的长是 0.5 米，把芦苇拉到岸边，它的顶端 $ B $ 恰好落到 $ D $ 点，求水池的深度 $ AC $。

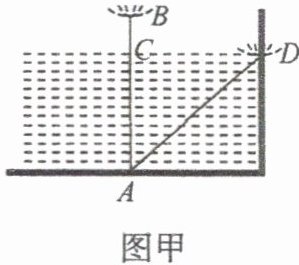
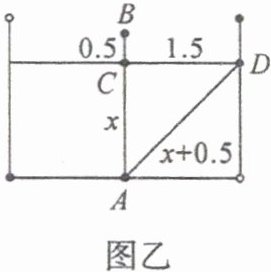
【剖析】先将实物模型转化为数学模型，如图乙。由题意可知 $\triangle ACD$ 中，$\angle ACD=90^{\circ}$，在 $\text{Rt} \triangle ACD$ 中，只知道 $ CD=1.5 $，这是典型的利用勾股定理“知二求一”的类型。
标准解题步骤如下（仅供参考）：
【解答】如图乙，根据勾股定理，$ AC^{2}+CD^{2}=AD^{2} $，设水深 $ AC=$$x$米，那么 $ AD=AB=AC+CB=$$x+0.5$，$x^{2}+1.5^{2}=(x+0.5)^{2}$，解之得 $ x=$2。故水深为2米。

答案： 【剖析】先将实物模型转化为数学模型，如图乙。由题意可知 $ \triangle ACD $ 中，$ \angle ACD=90^{\circ} $，在 $ \text{Rt} \triangle ACD $ 中，只知道 $ CD=1.5 $，这是典型的利用勾股定理“知二求一”的类型。
标准解题步骤如下（仅供参考）：
【解答】如图乙，根据勾股定理，$ AC^{2}+CD^{2}=AD^{2} $，设水深 $ AC=x $ 米，那么 $ AD=AB=AC+CB=x+0.5 $，$ x^{2}+1.5^{2}=(x+0.5)^{2} $，解之得 $ x=2 $。故水深为 2 米。