《2025年假期总动员年度系统复习八年级数学人教版四川师范大学出版社》

18. 如图,4 个小动物分别站在正方形场地的 4 个顶点,它们同时出发并以相同的速度沿场地边缘逆时针方向跑动. 当它们同时停止时,顺次连接 4 个动物所在地点围成的图形是什么形状? 为什么?

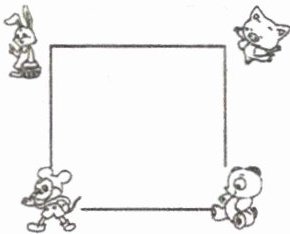
正方形，理由略

答案： 解:正方形，理由略.

19. 如图,平行四边形 ABCD 中,AC 和 BD 交于 O,EF 过 O 点交 AD 于 E,交 BC 于 F,HG 过 O 点交 AB 于 H,交 CD 于 G.
如果 EF 平分 $ \angle AOD $,HG 平分 $ \angle AOB $.
求证:四边形 EHFG 为菱形.
证明：∵OE 平分∠AOD，∠AOE=$\frac{1}{2}$∠AOD. ∵OH 平分∠AOB，∠AOH=$\frac{1}{2}$∠AOB. ∵∠AOD+∠AOB=180°，∴∠AOE+∠AOH=$\frac{1}{2}$×180°=90°即 HG⊥EF.
∵ABCD 为平行四边形，∴OA=OC，BO=OD，AD//BC，AB//CD. ∴∠DAO=∠BCO，∠ABO=∠ODC. ∴△AOE≌△OCF，△BHO≌△ODG. ∴OE=OF，OH=OG，∴四边形 HFGE 为菱形.

答案： 证明：
∵OE 平分∠AOD，∠AOE=$\frac{1}{2}$∠AOD.
∵OH 平分∠AOB，∠AOH=$\frac{1}{2}$∠AOB.
∵∠AOD+∠AOB=180°，
∴∠AOE+∠AOH=$\frac{1}{2}$×180°=90°即 HG⊥EF.
∵ABCD 为平行四边形，
∴OA=OC，BO=OD，AD//BC，AB//CD.
∴∠DAO=∠BCO，∠ABO=∠ODC.
∴△AOE≌△OCF，△BHO≌△ODG.
∴OE=OF，OH=OG，
∴四边形 HFGE 为菱形.

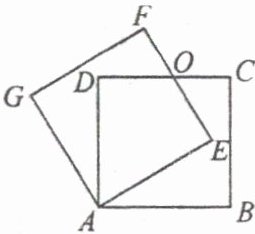
20. 如图,正方形 ABCD 绕点 A 逆时针旋转 $ n^{\circ} $ 后得到正方形 AEFG,边 EF 与 CD 交于点 O.
(1) 以图中已标有字母的点为端点连接两条线段(正方形的对角线除外),要求所连接的两条线段相交且互相垂直,并说明这两条线段互相垂直的理由;
所连接的两条线段是AO和DE
(2) 若正方形的边长为 2cm,重叠部分(四边形 AEOD)的面积为 $ \frac{4}{3}\sqrt{3}cm^{2} $,则旋转的角度 n 为30度?

答案：
解:
(1)AO⊥DE
证明:
∵在 Rt△ADO 与 Rt△AEO 中，AD=AE，AO=AO，
∴Rt△ADO≌Rt△AEO，
∴∠DAO=∠OAE(即 AO 平分∠DAE)
∴AO⊥DE(等腰三角形的三线合一)
(2)n = 30°.
理由:连接 AO，
∵四边形 AEOD 的面积为$\frac{4}{3}\sqrt{3}$cm²，
∴三角形 ADO 的面积为$\frac{2}{3}\sqrt{3}$cm²，
∵AD = 2，
∴DO = $\frac{2}{3}$$\sqrt{3}$，在 Rt△ADO 中，∠DAO = 30°，
∴∠EAD = 60°，∠EAB = 30°，即 n = 30°.