《2025年暑假乐园海南出版社八年级数学华师大版》

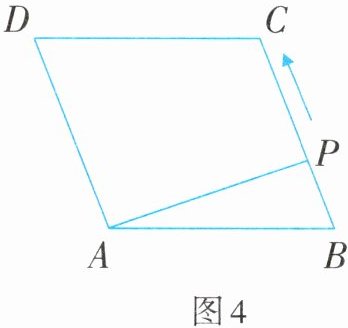
5. 如图4，在菱形ABCD中，∠B=60°，点P从点B出发，沿折线BC→CD方向移动，移动到点D停止.在△ABP形状的变化过程中，依次出现的特殊三角形是( ).

A. 直角三角形→等边三角形→等腰三角形→直角三角形
B. 直角三角形→等腰三角形→直角三角形→等边三角形
C. 直角三角形→等边三角形→直角三角形→等腰三角形
D. 等腰三角形→等边三角形→直角三角形→等腰三角形

答案： C

1. 在菱形ABCD中，∠A=60°，其周长为24cm，则菱形的面积为______cm².

答案： $1 8 \sqrt{3}$　　

2. 在菱形ABCD中，若AC=6，BD=8，则菱形ABCD的面积是______.

答案： 24

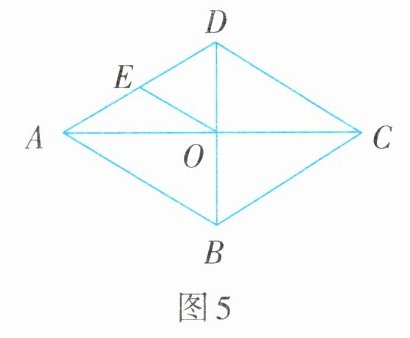
3. 如图5，菱形ABCD的对角线AC，BD相交于点O，E为边AD的中点，若OE=3，则菱形ABCD的周长为______.

答案： 24

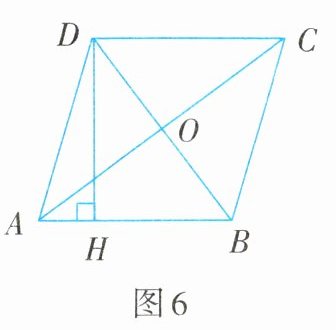
4. 如图6，在菱形ABCD中，对角线AC与BD相交于点O，且AC=8，BD=6，则菱形ABCD的高DH=______.

答案： $\dfrac{24}{5}$

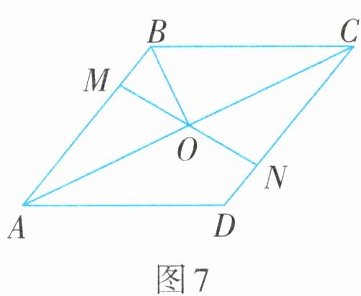
5. 如图7，在菱形ABCD中，M，N分别在边AB，CD上，且AM=CN，MN与AC交于点O，连接BO.若∠DAC=28°，则∠OBC=______.

答案： 62°

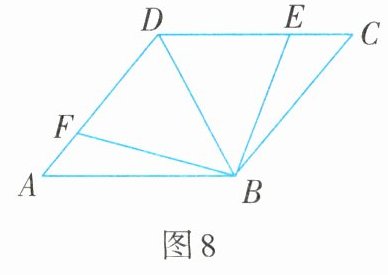
1. 如图8，E，F分别在菱形ABCD的边DC，DA上，且CE=AF. 求证：∠ABF=∠CBE.

答案： 【解析】：
因为四边形$ABCD$是菱形，所以$AB = BC$，$\angle A=\angle C$。
在$\triangle ABF$和$\triangle CBE$中，
$\begin{cases}AB = BC\\\angle A=\angle C\\AF = CE\end{cases}$
根据全等三角形的判定定理（$SAS$：两边及其夹角对应相等的三角形全等），可得$\triangle ABF\cong\triangle CBE$。
根据全等三角形的性质：全等三角形的对应角相等，所以$\angle ABF=\angle CBE$。
【答案】：证明过程如上述解析，可证得$\angle ABF = \angle CBE$。

2. 如图9，AE//BF，AC平分∠BAE，且交BF于点C，BD平分∠ABF，且交AE于点D，连接CD.
(1)求证：四边形ABCD是菱形；
(2)若∠ADB=30°，BD=6，求AD的长.

答案： $(1)$ 证明四边形$ABCD$是菱形
- **步骤一：利用平行线性质和角平分线性质得到相等的角**
已知$AE// BF$，根据“两直线平行，内错角相等”，可得$\angle ADB = \angle CBD$。
因为$BD$平分$\angle ABF$，所以$\angle ABD = \angle CBD$，从而$\angle ABD = \angle ADB$。
根据“等角对等边”，可得$AB = AD$。
同理，因为$AC$平分$\angle BAE$，$AE// BF$，可得$\angle BAC = \angle BCA$，进而$AB = BC$。
- **步骤二：证明四边形$ABCD$是平行四边形**
由$AE// BF$，即$AD// BC$，又因为$AD = AB$，$BC = AB$，所以$AD = BC$。
根据“一组对边平行且相等的四边形是平行四边形”，可知四边形$ABCD$是平行四边形。
- **步骤三：得出四边形$ABCD$是菱形**
又因为$AB = AD$，根据“一组邻边相等的平行四边形是菱形”，所以四边形$ABCD$是菱形。
### $(2)$ 求$AD$的长
- **步骤一：利用菱形的性质**
因为四边形$ABCD$是菱形，$BD = 6$，根据“菱形的对角线互相垂直且平分”，所以$AC\perp BD$，$OD=\frac{1}{2}BD = 3$。
- **步骤二：在$Rt\triangle AOD$中求解$AD$的长**
已知$\angle ADB = 30^{\circ}$，在$Rt\triangle AOD$中，$\cos\angle ADB=\frac{OD}{AD}$。
根据三角函数值$\cos30^{\circ}=\frac{\sqrt{3}}{2}$，则$AD=\frac{OD}{\cos\angle ADB}=\frac{3}{\cos30^{\circ}}=\frac{3}{\frac{\sqrt{3}}{2}} = 2\sqrt{3}$。