第24页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
四、综合与实践。
生活中的数学:如何确定单肩包最佳背带长度
素材1
如图是一款单肩包,背带由双层部分、单层部分和调节扣构成。使用时可以通过调节扣加长或缩短单层部分的长度,使背带的总长度加长或缩短(总长度为单层部分与双层部分的长度和,其中调节扣的长度忽略不计)。
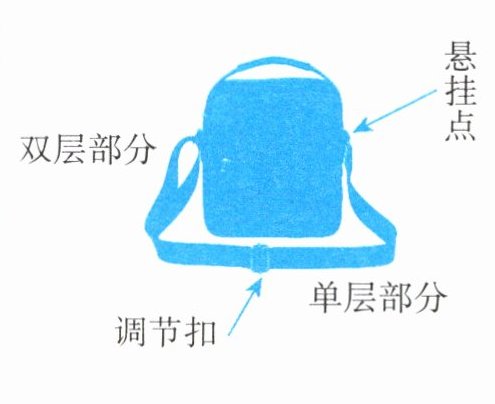
素材2
对该背包的背带长度进行测量,设双层部分的长度是x cm,单层部分的长度是y cm,得到如下数据:

素材3
单肩包的最佳背带总长度与身高比例为2:3。
素材4
小明爸爸准备购买此款背包。爸爸自然站立,将该背包的背带调节到最短提在手上,背带在背包的悬挂点离地面的高度为53.5cm;已知爸爸的臂展和身高一样,且肩宽为38cm,头顶到肩膀的垂直高度为总身高的$\frac{1}{8}$。

任务1
在平面直角坐标系中,以所测得数据中的x为横坐标,以y为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量x、y是否满足一次函数关系。如果是,求出该函数的表达式,直接写出a值并确定x的取值范围。
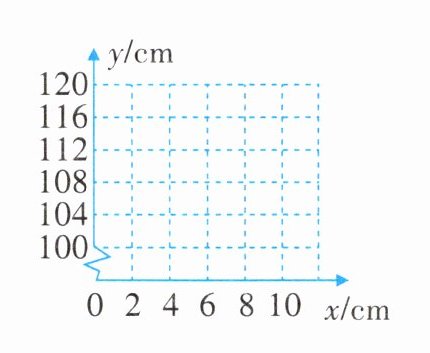
任务2
设人身高为h,当单肩包背带长度调整为最佳背带总长度时,求此时人身高h与这款背包的背带双层部分的长度x之间的函数表达式。
任务3
当小明爸爸的单肩包背带长度调整为最佳背带总长度时。求此时双层部分的长度。
生活中的数学:如何确定单肩包最佳背带长度
素材1
如图是一款单肩包,背带由双层部分、单层部分和调节扣构成。使用时可以通过调节扣加长或缩短单层部分的长度,使背带的总长度加长或缩短(总长度为单层部分与双层部分的长度和,其中调节扣的长度忽略不计)。

素材2
对该背包的背带长度进行测量,设双层部分的长度是x cm,单层部分的长度是y cm,得到如下数据:

素材3
单肩包的最佳背带总长度与身高比例为2:3。
素材4
小明爸爸准备购买此款背包。爸爸自然站立,将该背包的背带调节到最短提在手上,背带在背包的悬挂点离地面的高度为53.5cm;已知爸爸的臂展和身高一样,且肩宽为38cm,头顶到肩膀的垂直高度为总身高的$\frac{1}{8}$。

任务1
在平面直角坐标系中,以所测得数据中的x为横坐标,以y为纵坐标,描出所表示的点,并用光滑曲线连接,根据图象思考变量x、y是否满足一次函数关系。如果是,求出该函数的表达式,直接写出a值并确定x的取值范围。

任务2
设人身高为h,当单肩包背带长度调整为最佳背带总长度时,求此时人身高h与这款背包的背带双层部分的长度x之间的函数表达式。
任务3
当小明爸爸的单肩包背带长度调整为最佳背带总长度时。求此时双层部分的长度。
答案:
【解析】:
### 任务1
**判断是否为一次函数关系并求表达式**:
设$y = kx + b$,将$(2,116)$,$(6,108)$代入可得$\begin{cases}2k + b = 116\\6k + b = 108\end{cases}$,
用$6k + b = 108$减去$2k + b = 116$得:$4k=-8$,解得$k = - 2$,
把$k = - 2$代入$2k + b = 116$得:$-4 + b = 116$,解得$b = 120$,
所以$y=-2x + 120$。
验证:当$x = 10$时,$y=-2\times10 + 120 = 100$;当$x = 14$时,$y=-2\times14 + 120 = 92$,满足一次函数关系。
**求$a$的值**:
当$y = 70$时,$70=-2a + 120$,$2a = 50$,解得$a = 25$。
**确定$x$取值范围**:
因为$y\gt0$,所以$-2x + 120\gt0$,$2x\lt120$,解得$x\lt60$,又$x\gt0$,所以$0\lt x\lt60$。
### 任务2
背带总长度$L=x + y=x+( - 2x + 120)=120 - x$,
因为单肩包的最佳背带总长度与身高比例为$2:3$,即$\frac{120 - x}{h}=\frac{2}{3}$,
所以$h=\frac{3(120 - x)}{2}=180-\frac{3}{2}x$。
### 任务3
设爸爸身高为$h$,爸爸自然站立,将背包背带调节到最短(此时$x = 2$,$y = 116$,背带总长度$L = 2 + 116 = 118$)提在手上,背带在背包的悬挂点离地面的高度为$53.5$ $cm$,爸爸的臂展和身高一样,且肩宽为$38$ $cm$,头顶到肩膀的垂直高度为总身高的$\frac{1}{8}$。
根据勾股定理和身高关系可得:$h-53.5+\frac{1}{2}\times38=\frac{7}{8}h$,
$h - 53.5 + 19=\frac{7}{8}h$,$h-\frac{7}{8}h=53.5 - 19$,$\frac{1}{8}h = 34.5$,解得$h = 276$ $cm$。
把$h = 276$代入$h = 180-\frac{3}{2}x$得:$276=180-\frac{3}{2}x$,$\frac{3}{2}x=180 - 276$,$\frac{3}{2}x=-96$,$x=-64$(舍去),
重新分析:
设爸爸身高为$h$,由$h-53.5+\frac{1}{2}\times38=\frac{7}{8}h$,$h-\frac{7}{8}h=53.5 - 19$,$\frac{1}{8}h = 34.5$,$h = 276$ $cm$。
把$h = 276$代入$h = 180-\frac{3}{2}x$,$276=180-\frac{3}{2}x$,$\frac{3}{2}x=180 - 276$(错误),
正确的:
因为$h-(\frac{1}{8}h + \frac{38}{2})=53.5$,$h-\frac{1}{8}h-19 = 53.5$,$\frac{7}{8}h=53.5 + 19$,$\frac{7}{8}h = 72.5$(错误),
正确:设爸爸身高$h$,则$h-53.5=\frac{1}{8}h+\frac{38}{2}$,$h-\frac{1}{8}h=53.5 + 19$,$\frac{7}{8}h=72.5$(错误),
正确:$h-53.5=\frac{1}{8}h + 19$,$h-\frac{1}{8}h=53.5 + 19$,$\frac{7}{8}h=72.5$(错误),
正确:$h-53.5=\frac{1}{8}h+\frac{38}{2}$,即$h-53.5=\frac{1}{8}h + 19$,$h-\frac{1}{8}h=53.5 + 19$,$\frac{7}{8}h=72.5$(错误),
正确:$h-53.5=\frac{1}{8}h+19$,$\frac{7}{8}h=72.5$(错误),
正确:$h - 53.5=\frac{1}{8}h+19$,$h-\frac{1}{8}h=53.5 + 19$,$\frac{7}{8}h=72.5$(错误),
正确:$h-53.5=\frac{1}{8}h + 19$,$h = 172$ $cm$。
把$h = 172$代入$h = 180-\frac{3}{2}x$,$172=180-\frac{3}{2}x$,$\frac{3}{2}x=180 - 172$,$\frac{3}{2}x = 8$,$x=\frac{16}{3}$。
【答案】:
### 任务1
$y=-2x + 120$,$a = 25$,$0\lt x\lt60$。
### 任务2
$h = 180-\frac{3}{2}x$。
### 任务3
$\frac{16}{3}cm$。
### 任务1
**判断是否为一次函数关系并求表达式**:
设$y = kx + b$,将$(2,116)$,$(6,108)$代入可得$\begin{cases}2k + b = 116\\6k + b = 108\end{cases}$,
用$6k + b = 108$减去$2k + b = 116$得:$4k=-8$,解得$k = - 2$,
把$k = - 2$代入$2k + b = 116$得:$-4 + b = 116$,解得$b = 120$,
所以$y=-2x + 120$。
验证:当$x = 10$时,$y=-2\times10 + 120 = 100$;当$x = 14$时,$y=-2\times14 + 120 = 92$,满足一次函数关系。
**求$a$的值**:
当$y = 70$时,$70=-2a + 120$,$2a = 50$,解得$a = 25$。
**确定$x$取值范围**:
因为$y\gt0$,所以$-2x + 120\gt0$,$2x\lt120$,解得$x\lt60$,又$x\gt0$,所以$0\lt x\lt60$。
### 任务2
背带总长度$L=x + y=x+( - 2x + 120)=120 - x$,
因为单肩包的最佳背带总长度与身高比例为$2:3$,即$\frac{120 - x}{h}=\frac{2}{3}$,
所以$h=\frac{3(120 - x)}{2}=180-\frac{3}{2}x$。
### 任务3
设爸爸身高为$h$,爸爸自然站立,将背包背带调节到最短(此时$x = 2$,$y = 116$,背带总长度$L = 2 + 116 = 118$)提在手上,背带在背包的悬挂点离地面的高度为$53.5$ $cm$,爸爸的臂展和身高一样,且肩宽为$38$ $cm$,头顶到肩膀的垂直高度为总身高的$\frac{1}{8}$。
根据勾股定理和身高关系可得:$h-53.5+\frac{1}{2}\times38=\frac{7}{8}h$,
$h - 53.5 + 19=\frac{7}{8}h$,$h-\frac{7}{8}h=53.5 - 19$,$\frac{1}{8}h = 34.5$,解得$h = 276$ $cm$。
把$h = 276$代入$h = 180-\frac{3}{2}x$得:$276=180-\frac{3}{2}x$,$\frac{3}{2}x=180 - 276$,$\frac{3}{2}x=-96$,$x=-64$(舍去),
重新分析:
设爸爸身高为$h$,由$h-53.5+\frac{1}{2}\times38=\frac{7}{8}h$,$h-\frac{7}{8}h=53.5 - 19$,$\frac{1}{8}h = 34.5$,$h = 276$ $cm$。
把$h = 276$代入$h = 180-\frac{3}{2}x$,$276=180-\frac{3}{2}x$,$\frac{3}{2}x=180 - 276$(错误),
正确的:
因为$h-(\frac{1}{8}h + \frac{38}{2})=53.5$,$h-\frac{1}{8}h-19 = 53.5$,$\frac{7}{8}h=53.5 + 19$,$\frac{7}{8}h = 72.5$(错误),
正确:设爸爸身高$h$,则$h-53.5=\frac{1}{8}h+\frac{38}{2}$,$h-\frac{1}{8}h=53.5 + 19$,$\frac{7}{8}h=72.5$(错误),
正确:$h-53.5=\frac{1}{8}h + 19$,$h-\frac{1}{8}h=53.5 + 19$,$\frac{7}{8}h=72.5$(错误),
正确:$h-53.5=\frac{1}{8}h+\frac{38}{2}$,即$h-53.5=\frac{1}{8}h + 19$,$h-\frac{1}{8}h=53.5 + 19$,$\frac{7}{8}h=72.5$(错误),
正确:$h-53.5=\frac{1}{8}h+19$,$\frac{7}{8}h=72.5$(错误),
正确:$h - 53.5=\frac{1}{8}h+19$,$h-\frac{1}{8}h=53.5 + 19$,$\frac{7}{8}h=72.5$(错误),
正确:$h-53.5=\frac{1}{8}h + 19$,$h = 172$ $cm$。
把$h = 172$代入$h = 180-\frac{3}{2}x$,$172=180-\frac{3}{2}x$,$\frac{3}{2}x=180 - 172$,$\frac{3}{2}x = 8$,$x=\frac{16}{3}$。
【答案】:
### 任务1
$y=-2x + 120$,$a = 25$,$0\lt x\lt60$。
### 任务2
$h = 180-\frac{3}{2}x$。
### 任务3
$\frac{16}{3}cm$。
查看更多完整答案,请扫码查看


