《2025年暑假乐园海南出版社八年级数学华师大版》

5. 某人购进一批苹果到农贸市场零售，已知卖出的苹果数量与售价之间的关系如图3所示。若成本为5元/千克，现以8元卖出，挣得________元。

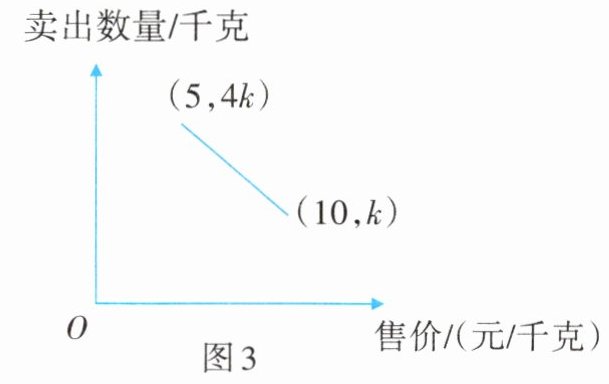
答案： $\frac{33}{5}k$

1. 已知y是关于x的一次函数，当x=3时，y=1；当x=-2时，y=-4。求这个一次函数的解析式。

答案： 【解析】：设该一次函数的解析式为$y = kx + b$（$k\neq0$）。
把$x = 3$，$y = 1$和$x = - 2$，$y = - 4$分别代入$y = kx + b$中，得到方程组$\begin{cases}3k + b = 1\\-2k + b = - 4\end{cases}$。
用第一个方程$3k + b = 1$减去第二个方程$-2k + b = - 4$，可得：
$(3k + b)-(-2k + b)=1-(-4)$
$3k + b + 2k - b = 1 + 4$
$5k = 5$，解得$k = 1$。
把$k = 1$代入$3k + b = 1$，得$3\times1 + b = 1$，即$3 + b = 1$，解得$b = 1 - 3=-2$。
所以这个一次函数的解析式为$y = x - 2$。
【答案】：$y = x - 2$

2. 求直线y=x+4和直线y=-x+4与x轴所围成的三角形的面积。

答案： 【解析】：
1. 首先求直线$y = x + 4$与$x$轴的交点：
当$y = 0$时，在$y=x + 4$中，$0=x + 4$，解得$x=-4$，所以直线$y = x + 4$与$x$轴的交点坐标为$A(-4,0)$。
2. 然后求直线$y=-x + 4$与$x$轴的交点：
当$y = 0$时，在$y=-x + 4$中，$0=-x + 4$，解得$x = 4$，所以直线$y=-x + 4$与$x$轴的交点坐标为$B(4,0)$。
3. 接着求两直线的交点：
联立两直线方程$\begin{cases}y=x + 4\\y=-x + 4\end{cases}$，将$y=x + 4$代入$y=-x + 4$中，得到$x + 4=-x + 4$。
移项可得$x+x=4 - 4$，即$2x=0$，解得$x = 0$。
把$x = 0$代入$y=x + 4$，得$y=4$，所以两直线的交点坐标为$C(0,4)$。
4. 最后求三角形的面积：
由$A(-4,0)$，$B(4,0)$可知$AB$的长度为$\vert4-(-4)\vert=\vert4 + 4\vert = 8$。
点$C(0,4)$到$x$轴的距离就是$C$点的纵坐标的绝对值，即三角形$ABC$中$AB$边上的高$h = 4$。
根据三角形面积公式$S=\frac{1}{2}\times底\times高$，这里底为$AB$，高为$h$，所以$S=\frac{1}{2}\times8\times4=16$。
【答案】：16