《2025年暑假乐园海南出版社八年级数学华师大版》

1. 已知反比例函数的图象经过点$P(2,-3)$。
（1）求该函数的解析式；
（2）若将点$P$沿$x$轴负方向平移$3$个单位长度，再沿$y$轴方向平移$n(n＞0)$个单位长度得到点$P'$，使点$P'$恰好在该函数的图象上，求$n$的值和点$P$沿$y$轴平移的方向。

答案： 【解析】：
（1）设反比例函数的解析式为$y = \frac{k}{x}(k\neq0)$，因为函数图象经过点$P(2,-3)$，把$x = 2$，$y=-3$代入$y=\frac{k}{x}$中，可得$-3=\frac{k}{2}$，解得$k = 2\times(-3)=-6$，所以该反比例函数的解析式为$y = -\frac{6}{x}$。
（2）点$P(2,-3)$沿$x$轴负方向平移$3$个单位长度，则横坐标变为$2 - 3=-1$，此时得到点$(-1,-3)$，再沿$y$轴方向平移$n(n\gt0)$个单位长度得到点$P'$，则$P'$的坐标为$(-1,-3 + n)$。
因为点$P'$恰好在反比例函数$y = -\frac{6}{x}$的图象上，把$x=-1$，$y=-3 + n$代入$y = -\frac{6}{x}$中，可得$-3 + n=-\frac{6}{-1}$，即$-3 + n = 6$，移项可得$n=6 + 3=9$。
因为$n = 9\gt0$，所以点$P$沿$y$轴正方向平移。
【答案】：（1）$y = -\frac{6}{x}$；（2）$n = 9$，点$P$沿$y$轴正方向平移。

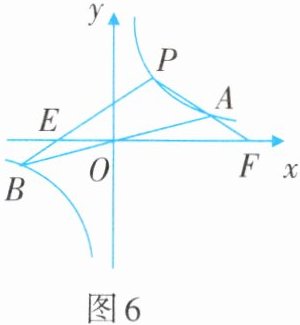
2. 如图6，双曲线$y_{1}=\frac {k_{1}}{x}$与直线$y_{2}=\frac {x}{k_{2}}$的图象交于$A$、$B$两点。已知点$A$的坐标为$(4,1)$，点$P(a,b)$是双曲线$y_{1}=\frac {k_{1}}{x}$上的任意一点，且$0＜a＜4$。
（1）分别求出$y_{1}$、$y_{2}$的函数表达式；
（2）连接$PA$，$PB$，得到$\triangle PAB$，若$4a=b$，求$\triangle PAB$的面积；
（3）当点$P$在双曲线$y_{1}=\frac {k_{1}}{x}$上运动时，设$PB$交$x$轴于点$E$，延长$PA$交$x$轴于点$F$，判断$PE$与$PF$的大小关系，并说明理由。

答案： 【解析】：
### $(1)$求$y_{1}$、$y_{2}$的函数表达式
已知点$A(4,1)$在双曲线$y_{1}=\frac{k_{1}}{x}$上，将$A(4,1)$代入$y_{1}=\frac{k_{1}}{x}$可得：
$1=\frac{k_{1}}{4}$，解得$k_{1}=4$，所以$y_{1}=\frac{4}{x}$。
又因为点$A(4,1)$在直线$y_{2}=\frac{x}{k_{2}}$上，将$A(4,1)$代入$y_{2}=\frac{x}{k_{2}}$可得：
$1 = \frac{4}{k_{2}}$，解得$k_{2}=4$，所以$y_{2}=\frac{x}{4}$。
### $(2)$求$\triangle PAB$的面积
因为点$P(a,b)$在双曲线$y_{1}=\frac{4}{x}$上，所以$ab = 4$。
又已知$4a = b$，将$b = 4a$代入$ab = 4$，可得$a\times4a = 4$，即$a^{2}=1$。
因为$0\lt a\lt4$，所以$a = 1$，则$b = 4$，即$P(1,4)$。
由于$A$、$B$关于原点对称，$A(4,1)$，所以$B(-4,-1)$。
设直线$PA$的解析式为$y=mx + n$，把$P(1,4)$，$A(4,1)$代入可得：
$\begin{cases}m + n = 4\\4m + n = 1\end{cases}$
用$4m + n = 1$减去$m + n = 4$得：$3m=-3$，解得$m=-1$。
把$m = - 1$代入$m + n = 4$得：$-1 + n = 4$，解得$n = 5$。
所以直线$PA$的解析式为$y=-x + 5$，令$y = 0$，则$0=-x + 5$，解得$x = 5$，即$F(5,0)$。
设直线$PB$的解析式为$y=px+q$，把$P(1,4)$，$B(-4,-1)$代入可得：
$\begin{cases}p + q = 4\\-4p + q = -1\end{cases}$
用$p + q = 4$减去$-4p + q = -1$得：$5p = 5$，解得$p = 1$。
把$p = 1$代入$p + q = 4$得：$1 + q = 4$，解得$q = 3$。
所以直线$PB$的解析式为$y=x + 3$，令$y = 0$，则$0=x + 3$，解得$x=-3$，即$E(-3,0)$。
$\triangle PAB$的面积$S_{\triangle PAB}=S_{\triangle PEF}-S_{\triangle AEF}$。
$EF=5-(-3)=8$，$P$到$x$轴的距离$h_{1}=4$，$A$到$x$轴的距离$h_{2}=1$。
$S_{\triangle PEF}=\frac{1}{2}\times EF\times h_{1}=\frac{1}{2}\times8\times4 = 16$，$S_{\triangle AEF}=\frac{1}{2}\times EF\times h_{2}=\frac{1}{2}\times8\times1 = 4$。
所以$S_{\triangle PAB}=16 - 4=12$。
### $(3)$判断$PE$与$PF$的大小关系
设$P(a,\frac{4}{a})$，直线$PA$的解析式为$y=k_{3}x + b_{3}$，把$P(a,\frac{4}{a})$，$A(4,1)$代入可得：
$\begin{cases}ak_{3}+b_{3}=\frac{4}{a}\\4k_{3}+b_{3}=1\end{cases}$
两式相减得：$(a - 4)k_{3}=\frac{4}{a}-1=\frac{4 - a}{a}$，则$k_{3}=-\frac{1}{a}$。
把$k_{3}=-\frac{1}{a}$代入$4k_{3}+b_{3}=1$得：$-\frac{4}{a}+b_{3}=1$，$b_{3}=1+\frac{4}{a}$。
所以直线$PA$的解析式为$y=-\frac{1}{a}x + 1+\frac{4}{a}$，令$y = 0$，则$0=-\frac{1}{a}x + 1+\frac{4}{a}$，解得$x=a + 4$，即$F(a + 4,0)$。
直线$PB$的解析式为$y=k_{4}x + b_{4}$，把$P(a,\frac{4}{a})$，$B(-4,-1)$代入可得：
$\begin{cases}ak_{4}+b_{4}=\frac{4}{a}\\-4k_{4}+b_{4}=-1\end{cases}$
两式相减得：$(a + 4)k_{4}=\frac{4}{a}+1=\frac{4 + a}{a}$，则$k_{4}=\frac{1}{a}$。
把$k_{4}=\frac{1}{a}$代入$-4k_{4}+b_{4}=-1$得：$-\frac{4}{a}+b_{4}=-1$，$b_{4}=-1+\frac{4}{a}$。
所以直线$PB$的解析式为$y=\frac{1}{a}x-1+\frac{4}{a}$，令$y = 0$，则$0=\frac{1}{a}x-1+\frac{4}{a}$，解得$x=a - 4$，即$E(a - 4,0)$。
过$P$作$PH\perp x$轴于$H$，$H(a,0)$。
$EH=a-(a - 4)=4$，$FH=(a + 4)-a=4$。
在$Rt\triangle PEH$和$Rt\triangle PFH$中，$PH$为公共边，$EH = FH$。
根据勾股定理$PE=\sqrt{PH^{2}+EH^{2}}$，$PF=\sqrt{PH^{2}+FH^{2}}$，所以$PE = PF$。
【答案】：
$(1)$$y_{1}=\boldsymbol{\frac{4}{x}}$，$y_{2}=\boldsymbol{\frac{x}{4}}$；
$(2)$$\boldsymbol{12}$；
$(3)$$\boldsymbol{PE = PF}$ 。