《2025年暑假乐园海南出版社八年级数学华师大版》

试一试，你一定很棒
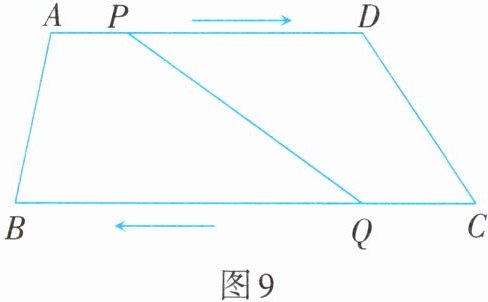
如图9，在四边形ABCD中，$ AD // BC $，$ AD = 24 \mathrm { cm } $，$ BC = 30 \mathrm { cm } $，点P从点A向点D以1 cm/s的速度运动，到点D即停止。点Q从点C向点B以2 cm/s的速度运动，到点B即停止。直线PQ将四边形ABCD截成两个四边形，分别为四边形ABQP和四边形PQCD，则当P，Q两点同时出发，几秒后所截得两个四边形中，其中一个四边形为平行四边形？

答案： 1. 设$t$秒后其中一个四边形为平行四边形：
因为$AD// BC$，若四边形$ABQP$是平行四边形，则$AP = BQ$。
已知$AP=t$，$CQ = 2t$，$BC = 30$，所以$BQ=30 - 2t$。
由$AP = BQ$可得方程$t=30 - 2t$。
解方程：
移项得$t + 2t=30$，即$3t = 30$，解得$t = 10$。
若四边形$PQCD$是平行四边形，则$PD = CQ$。
已知$AD = 24$，$AP=t$，所以$PD=24 - t$，$CQ = 2t$。
由$PD = CQ$可得方程$24 - t=2t$。
解方程：
移项得$2t + t=24$，即$3t = 24$，解得$t = 8$。
所以$8$秒或$10$秒后所截得两个四边形中，其中一个四边形为平行四边形。