《2025年暑假作业八年级数学人教版教育科学出版社》

7. 已知一次函数$y = 2x + b的图像经过P(0, - 1)$,则这个一次函数的表达式是( )。

A.$y = - x + 2$
B.$y = - 2x + 1$
C.$y = - x - 1$
D.$y = 2x - 1$

答案： 【解析】：已知一次函数$y = 2x + b$的图像经过点$P(0, -1)$，将点$P$的坐标代入函数表达式可得：$-1 = 2×0 + b$，解得$b=-1$。所以这个一次函数的表达式是$y = 2x - 1$。
【答案】：D

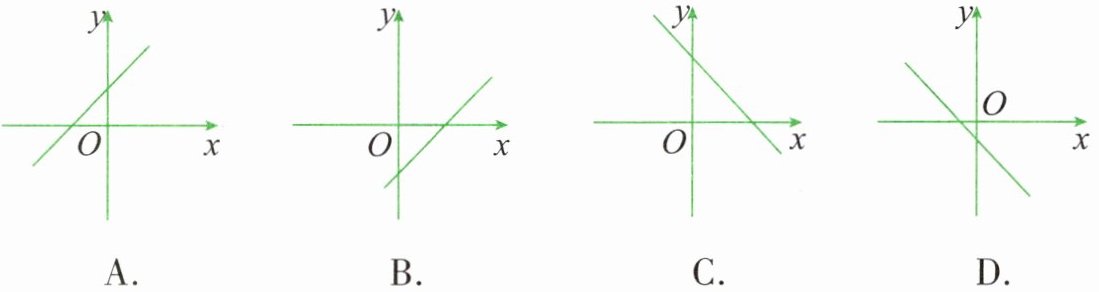
8. 正比例函数$y = kx(k \neq 0)的函数值y随x$的增大而增大,则一次函数$y = x + k$的图像大致是( )。

答案： 【解析】：
由于正比例函数$y=kx$（$k\neq0$）的函数值$y$随$x$的增大而增大，
由此我们可以得出$k＞0$。
接下来我们考虑一次函数$y=x+k$，
由于$k＞0$，所以$y=x+k$的图像在$y$轴上的截距$k$也是大于$0$的，
并且斜率为$1$（大于$0$），
因此函数图像是一个从左下到右上的直线，且在$y$轴上的截距大于$0$。
根据这个性质，我们可以确定答案是选项A中的图像。
【答案】：A

9. 计算$\sqrt{27} - \sqrt{\frac{1}{3}} = $____。

答案： 【解析】：
首先，我们将给定的根式化为最简形式。
$\sqrt{27} = \sqrt{9 × 3} = 3\sqrt{3}$
$\sqrt{\frac{1}{3}} = \frac{\sqrt{1}}{\sqrt{3}} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$
接下来，进行减法运算：
$3\sqrt{3} - \frac{\sqrt{3}}{3} = \frac{9\sqrt{3}}{3} - \frac{\sqrt{3}}{3} = \frac{8\sqrt{3}}{3}$
【答案】：$\frac{8\sqrt{3}}{3}$

10. 二次根式$\sqrt{\frac{1}{2}}$、$\sqrt{12}$、$\sqrt{30}$、$\sqrt{x + 2}$,$\sqrt{49x^{2}}$、$\sqrt{a^{2} + b^{2}}$中最简二次根式有____个。

答案： 【解析】：最简二次根式需满足被开方数不含分母且不含能开得尽方的因数或因式。
$\sqrt{\frac{1}{2}}$：被开方数含分母，不是最简二次根式。
$\sqrt{12}=\sqrt{4×3}=2\sqrt{3}$：被开方数含能开得尽方的因数 4，不是最简二次根式。
$\sqrt{30}$：被开方数 30 不含分母，且不含能开得尽方的因数或因式，是最简二次根式。
$\sqrt{x + 2}$：被开方数$x + 2$不含分母，且不含能开得尽方的因式，是最简二次根式。
$\sqrt{49x^{2}}=7|x|$：被开方数含能开得尽方的因数 49 和因式$x^2$，不是最简二次根式。
$\sqrt{a^{2} + b^{2}}$：被开方数$a^2 + b^2$不含分母，且不含能开得尽方的因式，是最简二次根式。
综上，最简二次根式有$\sqrt{30}$、$\sqrt{x + 2}$、$\sqrt{a^{2} + b^{2}}$，共 3 个。
【答案】：3

11. $a$、$b$、$c是\triangle ABC$三边的长,且满足$\sqrt{c^{2} - a^{2} - b^{2}} + |a - b| = 0$,则$\triangle ABC$的形状是____。

答案： 【解析】：
首先，由于$\sqrt{c^{2} - a^{2} - b^{2}} + |a - b| = 0$，
根据非负数的性质，我们知道$\sqrt{c^{2} - a^{2} - b^{2}}$和$|a - b|$都是非负数。
因此，要使它们的和为0，必须满足：
$\sqrt{c^{2} - a^{2} - b^{2}} = 0$
$|a - b| = 0$
从第一个方程，我们得到：
$c^{2} - a^{2} - b^{2} = 0$
$c^{2} = a^{2} + b^{2}$
这是勾股定理的逆定理，说明$\triangle ABC$是直角三角形。
从第二个方程，我们得到：
$a - b = 0$
$a = b$
这说明$\triangle ABC$的两边相等，即它是等腰三角形。
综合以上两点，$\triangle ABC$既是直角三角形又是等腰三角形，所以它是等腰直角三角形。
【答案】：等腰直角三角形

12. 菱形$ABCD的两条对角线AC$、$BD$的长度分别为 8cm 和 6cm,则菱形$ABCD$的周长是____。

答案： 【解析】：
由于菱形的对角线互相垂直且平分，我们可以知道对角线$AC$和$BD$相交于点$O$，并且$AO = \frac{1}{2}AC = 4cm$，$BO = \frac{1}{2}BD = 3cm$。
接下来，我们可以利用勾股定理来计算菱形的一边$AB$的长度。
根据勾股定理，在直角三角形中，直角边的平方和等于斜边的平方，即$AO^2 + BO^2 = AB^2$。
代入已知的$AO$和$BO$的值，我们得到：
$AB^2 = 4^2 + 3^2 = 16 + 9 = 25$
所以，$AB = \sqrt{25} = 5(cm)$。
由于菱形的四条边长度相等，所以菱形$ABCD$的周长为$4 × AB = 4 × 5 = 20(cm)$。
【答案】：20cm

13. 将直线$y = - x - 5$向上平移 5 个单位,得到直线____。

答案： 【解析】：根据一次函数图像平移规律“上加下减”，将直线$y = -x - 5$向上平移5个单位，只需在常数项上加上5。即平移后的直线解析式为$y = -x - 5 + 5 = -x$。
【答案】：$y=-x$

14. 如下图所示,在$□ ABCD$中,$DE \perp AB于点E$,$DF \perp BC于点F$,若$DE = 4$,$DF = 6$,$□ ABCD$的周长为 40,则$□ ABCD$面积是____。

答案： 【解析】：
设$AB = x$，$BC = y$，
由于平行四边形的周长为40，根据平行四边形的性质，对边相等，所以有：
$2(x + y) = 40$，
即$x + y = 20$，这是第一个方程。
由于$DE \perp AB$，$DF \perp BC$，且$DE = 4$，$DF = 6$，
根据平行四边形的面积公式，面积$S$可以表示为：
$S = AB × DE = BC × DF$，
即$4x = 6y$，
化简得：$2x = 3y$，这是第二个方程。
接下来，我们解这个二元一次方程组：
$\begin{cases}x + y = 20 \\2x = 3y\end{cases}$
解这个方程组，我们得到：
$\begin{cases}x = 12 \\y = 8\end{cases}$
最后，我们用求得的$x$值（即$AB$的长度）和已知的$DE$值（即$AB$边上的高）来计算平行四边形的面积：
$S = AB × DE = 12 × 4 = 48$。
【答案】：48

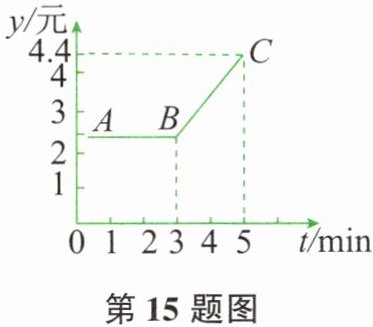
15. 如下图所示,折线$ABC是甲地向乙地打长途电话所需付的电话费y$(元)与通话时间$t(\min)$之间的函数关系图像。当$t\geq 3$时,该图像的解析式是____。从图中可知,通话 2min 需付电话费____元；通话 7min 需付电话费____元。

答案： 【解析】：由图像可知，当$t\geq 3$时，图像是线段$BC$。设线段$BC$的解析式为$y = kt + b$（$k\neq 0$）。
从图中读取$B$点坐标为$(3, 2)$，$C$点坐标为$(5, 4.4)$。
将$B(3, 2)$代入$y = kt + b$，得$3k + b = 2$；将$C(5, 4.4)$代入，得$5k + b = 4.4$。
用$5k + b = 4.4$减去$3k + b = 2$，可得：$2k = 2.4$，解得$k = 1.2$。
将$k = 1.2$代入$3k + b = 2$，得$3×1.2 + b = 2$，即$3.6 + b = 2$，解得$b = -1.6$。
所以当$t\geq 3$时，解析式为$y = 1.2t - 1.6$。
通话$2$分钟时，$t = 2 ＜ 3$，对应图像上的线段$AB$，此时$y = 2$元。
通话$7$分钟时，$t = 7\geq 3$，代入解析式$y = 1.2×7 - 1.6 = 8.4 - 1.6 = 6.8$元。
【答案】：$y = 1.2t - 1.6$；2；6.8