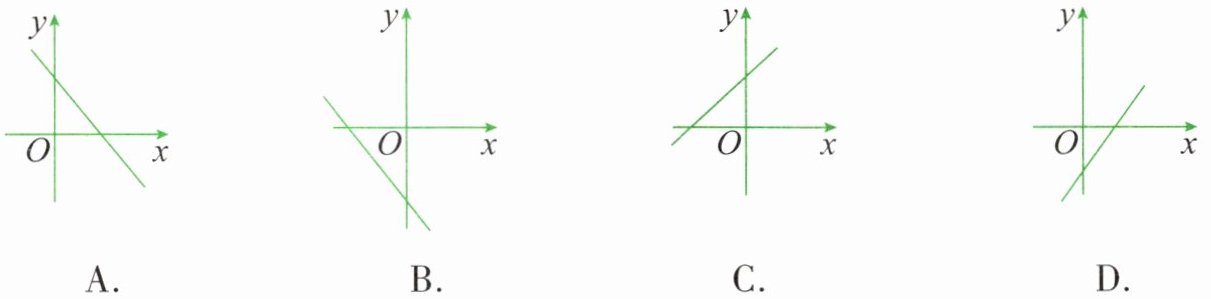
6. 已知一次函数$ y = kx + b $,$ y 随着 x $的增大而减小,且$ kb < 0 $,则在直角坐标系内它的大致图像是( )。

答案:
【解析】:因为一次函数$y = kx + b$中$y$随着$x$的增大而减小,所以$k < 0$。又因为$kb < 0$,$k$为负数,那么$b$必须为正数,即函数与$y$轴的交点在正半轴。一次函数$k < 0$时图像从左到右下降,$b > 0$时交$y$轴正半轴,符合条件的图像是选项A。
【答案】:A
【答案】:A
7. 在一次函数$ y = (2 - k)x + 1 $中,$ y 随 x $的增大而增大,则$ k $的取值范围为______。
答案:
【解析】:对于一次函数$y = mx + b$($m$、$b$为常数,$m\neq0$),当$m>0$时,$y$随$x$的增大而增大。在函数$y=(2 - k)x + 1$中,斜率$m = 2 - k$。因为$y$随$x$的增大而增大,所以$2 - k>0$,解得$k<2$。
【答案】:$k < 2$
【答案】:$k < 2$
8. 已知正比例函数$ y = kx 的图像经过点 A(-1,2) $,则正比例函数的解析式为______。
答案:
【解析】:因为正比例函数$y = kx$的图像经过点$A(-1,2)$,所以将点$A$的坐标代入函数解析式中,可得$2 = k×(-1)$,解得$k=-2$。因此,该正比例函数的解析式为$y = -2x$。
【答案】:$y = -2x$
【答案】:$y = -2x$
9. 写出一个图像经过第一、第三象限的正比例函数解析式:______。
答案:
【解析】:
正比例函数的一般形式为 $y = kx$,其中 $k$ 是比例系数。
因为图像需要经过第一、第三象限,根据正比例函数的性质,当 $k > 0$ 时,图像会经过第一、第三象限。
因此,需要选择一个 $k > 0$ 的值。
最简单的选择是 $k = 1$,此时正比例函数解析式为 $y = x$。
当然,$k$ 也可以取其他正数,如 $2, 3, 0.5,$ 等,只要保证 $k > 0$ 即可。
【答案】:$y = x$(答案不唯一,$k > 0$ 的其他值也可)
正比例函数的一般形式为 $y = kx$,其中 $k$ 是比例系数。
因为图像需要经过第一、第三象限,根据正比例函数的性质,当 $k > 0$ 时,图像会经过第一、第三象限。
因此,需要选择一个 $k > 0$ 的值。
最简单的选择是 $k = 1$,此时正比例函数解析式为 $y = x$。
当然,$k$ 也可以取其他正数,如 $2, 3, 0.5,$ 等,只要保证 $k > 0$ 即可。
【答案】:$y = x$(答案不唯一,$k > 0$ 的其他值也可)
10. 一次函数$ y = -2x + 4 的图像与 x $轴的交点坐标是______,与$ y $轴的交点坐标是______。
答案:
【解析】:要求一次函数$y = -2x + 4$与$x$轴的交点坐标,因为与$x$轴相交时$y = 0$,所以令$y = 0$,则有$0=-2x + 4$,解方程可得$2x=4$,$x = 2$,所以与$x$轴的交点坐标是$(2,0)$。
要求与$y$轴的交点坐标,因为与$y$轴相交时$x = 0$,将$x = 0$代入函数可得$y=-2×0 + 4=4$,所以与$y$轴的交点坐标是$(0,4)$。
【答案】:(2,0),(0,4)
要求与$y$轴的交点坐标,因为与$y$轴相交时$x = 0$,将$x = 0$代入函数可得$y=-2×0 + 4=4$,所以与$y$轴的交点坐标是$(0,4)$。
【答案】:(2,0),(0,4)
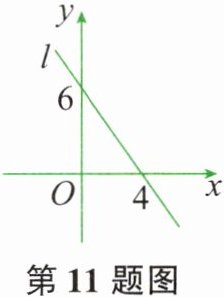
11. 如图所示,直线$ l 为一次函数 y = kx + b $的图像,则$ b = $______,$ k = $______。

答案:
【解析】:
由图像可知直线$l$经过点$(0,6)$和点$(4,0)$。
将点$(0,6)$代入$y = kx + b$,可得:
$6 = k×0 + b$,解得$b = 6$。
将点$(4,0)$和$b = 6$代入$y = kx + b$,可得:
$0 = 4k + 6$,
移项可得$4k = -6$,
解得$k = -\frac{3}{2}$。
【答案】:$b = 6$,$k = -\frac{3}{2}$
由图像可知直线$l$经过点$(0,6)$和点$(4,0)$。
将点$(0,6)$代入$y = kx + b$,可得:
$6 = k×0 + b$,解得$b = 6$。
将点$(4,0)$和$b = 6$代入$y = kx + b$,可得:
$0 = 4k + 6$,
移项可得$4k = -6$,
解得$k = -\frac{3}{2}$。
【答案】:$b = 6$,$k = -\frac{3}{2}$
12. 为保护学生视力,课桌椅的高度都是按一定的关系配套设计的。研究表明:假设课桌的高度为$ y \ cm $,椅子的高度为$ x \ cm $,则$ y 应是 x $的一次函数,下表列出两套符合条件的课桌椅的高度。
| |第一套|第二套|
|椅子高度$ x(cm) $|40|37|
|课桌高度$ y(cm) $|75|70|
(1)请确定$ y 与 x $的函数关系式。
(2)现有一把高$ 39 \ cm 的椅子和一张高 78.2 \ cm $的课桌,它们是否配套? 为什么?
| |第一套|第二套|
|椅子高度$ x(cm) $|40|37|
|课桌高度$ y(cm) $|75|70|
(1)请确定$ y 与 x $的函数关系式。
(2)现有一把高$ 39 \ cm 的椅子和一张高 78.2 \ cm $的课桌,它们是否配套? 为什么?
答案:
【解析】:
(1) 设$y$与$x$的关系为一次函数,即$y = kx + b$。
根据表格中的数据,可以列出以下方程组:
$\begin{cases}75 = 40k + b \\70 = 37k + b\end{cases}$
解这个方程组,首先用第一个方程减去第二个方程得到:
$75 - 70 = 40k - 37k$
$5 = 3k$
$k = \frac{5}{3}$
将$k = \frac{5}{3}$代入第一个方程$75 = 40k + b$,解得:
$75 = 40 × \frac{5}{3} + b$
$75 = \frac{200}{3} + b$
$b = 75 - \frac{200}{3}$
$b = \frac{225}{3} - \frac{200}{3}$
$b = \frac{25}{3}$
所以,$y$与$x$的函数关系式为:
$y = \frac{5}{3}x + \frac{25}{3}$
为了更方便使用,可以将其化为整数系数的形式:
$y = \frac{5}{3}(x + 5)$
即:
$y = \frac{5x + 25}{3}$
(2) 将$x = 39$代入上面求得的函数关系式$y = \frac{5x + 25}{3}$中,得到:
$y = \frac{5 × 39 + 25}{3}$
$y = \frac{195 + 25}{3}$
$y = \frac{220}{3}$
$y \approx 73.33$
由于$73.33 \neq 78.2$,所以一把高$39cm$的椅子和一张高$78.2cm$的课桌不配套。
【答案】:
(1)$y = \frac{5x + 25}{3}$
(2)不配套,因为当$x = 39$时,按设计$y$应为约$73.33$,而实际课桌高度为$78.2cm$,所以不配套。
(1) 设$y$与$x$的关系为一次函数,即$y = kx + b$。
根据表格中的数据,可以列出以下方程组:
$\begin{cases}75 = 40k + b \\70 = 37k + b\end{cases}$
解这个方程组,首先用第一个方程减去第二个方程得到:
$75 - 70 = 40k - 37k$
$5 = 3k$
$k = \frac{5}{3}$
将$k = \frac{5}{3}$代入第一个方程$75 = 40k + b$,解得:
$75 = 40 × \frac{5}{3} + b$
$75 = \frac{200}{3} + b$
$b = 75 - \frac{200}{3}$
$b = \frac{225}{3} - \frac{200}{3}$
$b = \frac{25}{3}$
所以,$y$与$x$的函数关系式为:
$y = \frac{5}{3}x + \frac{25}{3}$
为了更方便使用,可以将其化为整数系数的形式:
$y = \frac{5}{3}(x + 5)$
即:
$y = \frac{5x + 25}{3}$
(2) 将$x = 39$代入上面求得的函数关系式$y = \frac{5x + 25}{3}$中,得到:
$y = \frac{5 × 39 + 25}{3}$
$y = \frac{195 + 25}{3}$
$y = \frac{220}{3}$
$y \approx 73.33$
由于$73.33 \neq 78.2$,所以一把高$39cm$的椅子和一张高$78.2cm$的课桌不配套。
【答案】:
(1)$y = \frac{5x + 25}{3}$
(2)不配套,因为当$x = 39$时,按设计$y$应为约$73.33$,而实际课桌高度为$78.2cm$,所以不配套。
查看更多完整答案,请扫码查看


