《2025年暑假作业八年级数学人教版教育科学出版社》

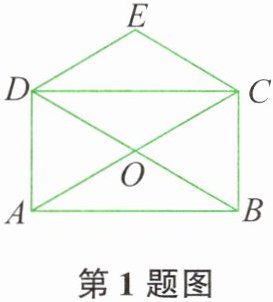
1. 如图所示,矩形 $ABCD$ 的对角线 $AC$、$BD$ 相交于点 $O$,$CE// BD$,$DE// AC$。若 $AC = 4$,则四边形 $CODE$ 的周长是( )。


A.$4$
B.$6$
C.$8$
D.$10$

答案： 【解析】：在矩形 $ABCD$ 中，对角线 $AC$ 与 $BD$ 相交于点 $O$，根据矩形的性质，对角线相等且互相平分，所以 $AC = BD = 4$，且 $OA = OC = \frac{1}{2}AC = 2$，$OB = OD = \frac{1}{2}BD = 2$。
因为 $CE // BD$，$DE // AC$，所以四边形 $CODE$ 是平行四边形（两组对边分别平行的四边形是平行四边形）。
又因为 $OC = OD = 2$（矩形对角线互相平分且相等），所以平行四边形 $CODE$ 的邻边相等，因此四边形 $CODE$ 是菱形（邻边相等的平行四边形是菱形）。
菱形的四条边都相等，所以 $CO = OD = DE = EC = 2$，则四边形 $CODE$ 的周长为 $4 × 2 = 8$。
【答案】：C

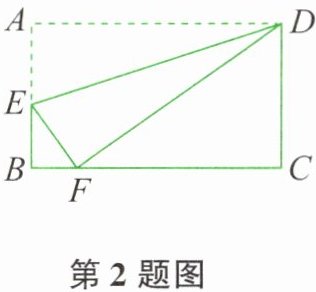
2. 如图所示,$E$ 在矩形 $ABCD$ 的边 $AB$ 上,将矩形 $ABCD$ 沿直线 $DE$ 折叠,点 $A$ 恰好落在 $BC$ 上的点 $F$ 处。若 $AE = 5$,$BF = 3$,则 $CD$ 的长是( )。


A.$7$
B.$8$
C.$9$
D.$10$

答案： 【解析】：
1. 折叠过程：将矩形 $ABCD$ 沿直线 $DE$ 折叠，使得点 $A$ 落在 $BC$ 边上的点 $F$ 处。
2. 折叠后，点 $A$ 和点 $F$ 关于直线 $DE$ 对称，因此 $AE = EF = 5$。
3. 在直角三角形 $EBF$ 中，已知 $BF = 3$，利用勾股定理计算 $BE$：
$BE = \sqrt{EF^2 - BF^2} = \sqrt{5^2 - 3^2} = \sqrt{25 - 9} = \sqrt{16} = 4$。
4. 由此可得 $AB = AE + BE = 5 + 4 = 9$。
5. 因为 $ABCD$ 是矩形，所以 $CD = AB = 9$。
【答案】：
C

3. 下列性质中矩形具有而一般平行四边形不具有的是( )。

A.有三个角是直角
B.对角线互相平分
C.有两条边相等
D.对角线互相垂直

答案： 【解析】：
A. 矩形的定义是四个角都是直角的平行四边形，所以矩形有三个角是直角（实际上四个角都是直角）。而一般的平行四边形并不保证有三个直角，所以选项A是矩形具有而一般平行四边形不具有的性质。
B. 对于对角线互相平分这一性质，平行四边形和矩形都满足，因为它们的对角线都会互相平分。所以选项B不是矩形独有的性质。
C. 有两条边相等这一性质，在平行四边形中也可能出现，例如菱形。所以选项C不是矩形独有的性质。
D. 对角线互相垂直这一性质，在平行四边形中不一定成立，但在矩形中也不一定成立（只有当矩形是正方形时才成立）。所以选项D不是矩形独有的性质。
综上所述，只有选项A是矩形具有而一般平行四边形不具有的性质。
【答案】：A

4. 四边形 $ABCD$ 的对角线 $AC$ 与 $BD$ 互相垂直,则下列结论中正确的是( )。

A.当 $AC = BD$ 时,四边形 $ABCD$ 是矩形
B.当 $AB = AD$,$CB = CD$ 时,四边形 $ABCD$ 是菱形
C.当 $AB = AD = BC$ 时,四边形 $ABCD$ 是菱形
D.当 $AC = BD$,$AD = AB$ 时,四边形 $ABCD$ 是正方形

答案： 【解析】：对于选项A，对角线互相垂直且相等的四边形不一定是矩形，矩形的对角线相等但不垂直（除非是正方形这种特殊矩形），所以A错误。
对于选项B，当$AB = AD$，$CB = CD$时，点A在BD的垂直平分线上，点C也在BD的垂直平分线上，因此AC垂直平分BD，但仅能说明AC是BD的垂直平分线，无法保证AC与BD互相平分，所以四边形ABCD不一定是平行四边形，更不是菱形，B错误。
对于选项C，设AC与BD交于点O。因为$AB = AD$，所以$\triangle ABD$是等腰三角形，又AC⊥BD，根据等腰三角形三线合一，可得BO=DO。同理，因为$AB = BC$，$\triangle ABC$是等腰三角形，AC⊥BD，可得AO=CO。因此AC与BD互相平分，四边形ABCD是平行四边形。又因为AC⊥BD，所以平行四边形ABCD是菱形，C正确。
对于选项D，AC=BD且AD=AB，对角线相等且有一组邻边相等，但对角线垂直不能保证四边形是平行四边形，更不是正方形，D错误。
【答案】：C