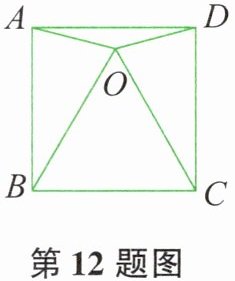
12. 如图所示,已知在正方形 $ABCD$ 中,$AO = DO$,$CO = CD$,$\angle AOD = 150^{\circ}$,则 $\angle BOC= $______。

答案:
【解析】:设正方形 $ABCD$ 的边长为 $a$,连接 $AC$。在正方形中,$AC = \sqrt{2}a$,$\angle ADC = 90^{\circ}$。
因为 $AO = DO$,$\angle AOD = 150^{\circ}$,设 $AO = DO = x$,在$\triangle AOD$中,由余弦定理得:$AD^2 = AO^2 + DO^2 - 2 \cdot AO \cdot DO \cdot \cos \angle AOD$,即$a^2 = x^2 + x^2 - 2x^2 \cos 150^{\circ}$。
$\cos 150^{\circ} = -\frac{\sqrt{3}}{2}$,代入得:$a^2 = 2x^2 - 2x^2 \left(-\frac{\sqrt{3}}{2}\right) = 2x^2 + \sqrt{3}x^2 = x^2(2 + \sqrt{3})$,所以$x^2 = \frac{a^2}{2 + \sqrt{3}} = a^2(2 - \sqrt{3})$(分母有理化),则$x = a\sqrt{2 - \sqrt{3}}$。
因为 $CO = CD = a$,在$\triangle COD$中,$CO = CD = a$,$DO = x = a\sqrt{2 - \sqrt{3}}$,由余弦定理求$\angle OCD$:$DO^2 = CO^2 + CD^2 - 2 \cdot CO \cdot CD \cdot \cos \angle OCD$,即$a^2(2 - \sqrt{3}) = a^2 + a^2 - 2a^2 \cos \angle OCD$。
化简得:$2 - \sqrt{3} = 2 - 2\cos \angle OCD$,所以$2\cos \angle OCD = \sqrt{3}$,$\cos \angle OCD = \frac{\sqrt{3}}{2}$,则$\angle OCD = 30^{\circ}$。
在正方形中,$\angle BCD = 90^{\circ}$,所以$\angle BCO = \angle BCD - \angle OCD = 90^{\circ} - 30^{\circ} = 60^{\circ}$。
在$\triangle BOC$中,$BC = CD = a$,$CO = a$,$\angle BCO = 60^{\circ}$,所以$\triangle BOC$是等边三角形(有一个角是$60^{\circ}$的等腰三角形是等边三角形),因此$\angle BOC = 60^{\circ}$。
【答案】:60°
因为 $AO = DO$,$\angle AOD = 150^{\circ}$,设 $AO = DO = x$,在$\triangle AOD$中,由余弦定理得:$AD^2 = AO^2 + DO^2 - 2 \cdot AO \cdot DO \cdot \cos \angle AOD$,即$a^2 = x^2 + x^2 - 2x^2 \cos 150^{\circ}$。
$\cos 150^{\circ} = -\frac{\sqrt{3}}{2}$,代入得:$a^2 = 2x^2 - 2x^2 \left(-\frac{\sqrt{3}}{2}\right) = 2x^2 + \sqrt{3}x^2 = x^2(2 + \sqrt{3})$,所以$x^2 = \frac{a^2}{2 + \sqrt{3}} = a^2(2 - \sqrt{3})$(分母有理化),则$x = a\sqrt{2 - \sqrt{3}}$。
因为 $CO = CD = a$,在$\triangle COD$中,$CO = CD = a$,$DO = x = a\sqrt{2 - \sqrt{3}}$,由余弦定理求$\angle OCD$:$DO^2 = CO^2 + CD^2 - 2 \cdot CO \cdot CD \cdot \cos \angle OCD$,即$a^2(2 - \sqrt{3}) = a^2 + a^2 - 2a^2 \cos \angle OCD$。
化简得:$2 - \sqrt{3} = 2 - 2\cos \angle OCD$,所以$2\cos \angle OCD = \sqrt{3}$,$\cos \angle OCD = \frac{\sqrt{3}}{2}$,则$\angle OCD = 30^{\circ}$。
在正方形中,$\angle BCD = 90^{\circ}$,所以$\angle BCO = \angle BCD - \angle OCD = 90^{\circ} - 30^{\circ} = 60^{\circ}$。
在$\triangle BOC$中,$BC = CD = a$,$CO = a$,$\angle BCO = 60^{\circ}$,所以$\triangle BOC$是等边三角形(有一个角是$60^{\circ}$的等腰三角形是等边三角形),因此$\angle BOC = 60^{\circ}$。
【答案】:60°
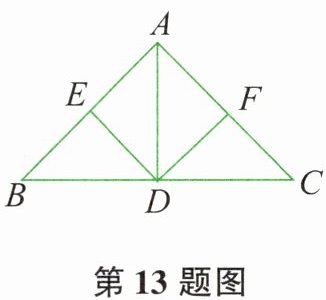
13. 如图所示,在 $\triangle ABC$ 中,$AD\perp BC$ 于点 $D$,$E$、$F$ 分别是 $AB$、$AC$ 的中点,当 $\triangle ABC$ 满足条件______时,四边形 $AEDF$ 是菱形。

答案:
【解析】:在$\triangle ABC$中,$AD\perp BC$,$E$、$F$分别是$AB$、$AC$的中点。根据直角三角形斜边中线定理,在$Rt\triangle ABD$中,$E$为$AB$中点,所以$DE=\frac{1}{2}AB=AE$;在$Rt\triangle ACD$中,$F$为$AC$中点,所以$DF=\frac{1}{2}AC=AF$。
因为$E$、$F$是$AB$、$AC$中点,所以$EF$是$\triangle ABC$的中位线,$EF// BC$且$EF=\frac{1}{2}BC$,同时$AD\perp BC$,所以$EF\perp AD$。
要使四边形$AEDF$是菱形,需四边相等。已知$AE=DE$,$AF=DF$,所以只需$AE=AF$,即$\frac{1}{2}AB=\frac{1}{2}AC$,可得$AB=AC$。此时$AE=AF=DE=DF$,且$EF\perp AD$,四边形$AEDF$为菱形。
【答案】:$AB=AC$
因为$E$、$F$是$AB$、$AC$中点,所以$EF$是$\triangle ABC$的中位线,$EF// BC$且$EF=\frac{1}{2}BC$,同时$AD\perp BC$,所以$EF\perp AD$。
要使四边形$AEDF$是菱形,需四边相等。已知$AE=DE$,$AF=DF$,所以只需$AE=AF$,即$\frac{1}{2}AB=\frac{1}{2}AC$,可得$AB=AC$。此时$AE=AF=DE=DF$,且$EF\perp AD$,四边形$AEDF$为菱形。
【答案】:$AB=AC$
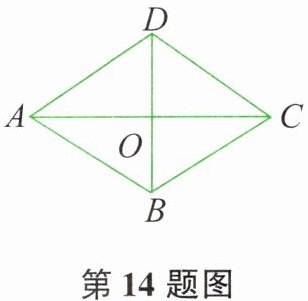
14. 如图所示,四边形 $ABCD$ 的四条边都相等,对角线 $AC$ 与 $BD$ 相交于点 $O$。若不增加任何字母与辅助线,要使得四边形 $ABCD$ 是正方形,还需增加的一个条件是______。

答案:
【解析】:
已知四边形$ABCD$的四条边都相等,根据菱形的判定定理:四条边都相等的四边形是菱形,所以四边形$ABCD$是菱形。
要使菱形成为正方形,根据正方形的判定定理,菱形中有一个角是直角或者对角线相等时,这个菱形就是正方形。
在本题不增加任何字母与辅助线的条件下,可以从角和对角线这两个方面来考虑添加条件。
若添加条件$\angle DAB = 90^{\circ}$,因为四边形$ABCD$是菱形,有一个角是直角的菱形是正方形,所以四边形$ABCD$是正方形;
若添加条件$AC = BD$,因为四边形$ABCD$是菱形,对角线相等的菱形是正方形,所以四边形$ABCD$是正方形。
【答案】:$\angle DAB = 90^{\circ}$(或$AC = BD$ )
已知四边形$ABCD$的四条边都相等,根据菱形的判定定理:四条边都相等的四边形是菱形,所以四边形$ABCD$是菱形。
要使菱形成为正方形,根据正方形的判定定理,菱形中有一个角是直角或者对角线相等时,这个菱形就是正方形。
在本题不增加任何字母与辅助线的条件下,可以从角和对角线这两个方面来考虑添加条件。
若添加条件$\angle DAB = 90^{\circ}$,因为四边形$ABCD$是菱形,有一个角是直角的菱形是正方形,所以四边形$ABCD$是正方形;
若添加条件$AC = BD$,因为四边形$ABCD$是菱形,对角线相等的菱形是正方形,所以四边形$ABCD$是正方形。
【答案】:$\angle DAB = 90^{\circ}$(或$AC = BD$ )
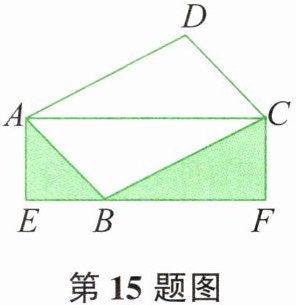
15. 如图所示,$□ ABCD$ 的顶点 $B$ 在矩形 $AEFC$ 的边 $EF$ 上,点 $B$ 与点 $E$、$F$ 不重合。若 $\triangle ACD$ 的面积为 $3$,则图中阴影部分两个三角形面积之和是______。

答案:
【解析】:在平行四边形 $ABCD$ 中,$AD = BC$,$AB = CD$,且对角线 $AC$ 将平行四边形分成两个面积相等的三角形,即 $S_{\triangle ABC} = S_{\triangle ACD}$。已知 $S_{\triangle ACD} = 3$,所以 $S_{\triangle ABC} = 3$。
矩形 $AEFC$ 中,$AC$ 是对角线,矩形的面积 $S_{矩形AEFC} = AC ×$ 高(以 $AC$ 为底时)。由于 $B$ 在 $EF$ 上,$\triangle ABC$ 以 $AC$ 为底时,其高与矩形 $AEFC$ 以 $AC$ 为底时的高相等(因为 $EF // AC$),所以 $S_{矩形AEFC} = 2S_{\triangle ABC} = 2 × 3 = 6$。
阴影部分为 $\triangle ABE$ 和 $\triangle CBF$,它们的面积之和等于矩形 $AEFC$ 的面积减去 $\triangle ABC$ 的面积,即 $S_{阴影} = S_{矩形AEFC} - S_{\triangle ABC} = 6 - 3 = 3$。
【答案】:3
矩形 $AEFC$ 中,$AC$ 是对角线,矩形的面积 $S_{矩形AEFC} = AC ×$ 高(以 $AC$ 为底时)。由于 $B$ 在 $EF$ 上,$\triangle ABC$ 以 $AC$ 为底时,其高与矩形 $AEFC$ 以 $AC$ 为底时的高相等(因为 $EF // AC$),所以 $S_{矩形AEFC} = 2S_{\triangle ABC} = 2 × 3 = 6$。
阴影部分为 $\triangle ABE$ 和 $\triangle CBF$,它们的面积之和等于矩形 $AEFC$ 的面积减去 $\triangle ABC$ 的面积,即 $S_{阴影} = S_{矩形AEFC} - S_{\triangle ABC} = 6 - 3 = 3$。
【答案】:3
16. 如图所示,在 $\triangle ABC$ 中,$AD$ 是角平分线,过点 $D$ 作 $DE// AC$,$DF// AB$。
求证:四边形 $AEDF$ 是菱形。
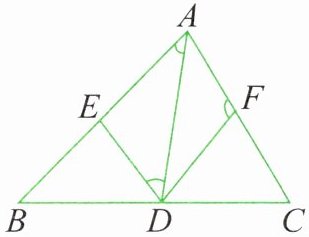
求证:四边形 $AEDF$ 是菱形。

答案:
【解析】:
证明:
$\because DE// AC,DF// AB$,
根据两组对边分别平行的四边形是平行四边形,
$\therefore$四边形$AEDF$是平行四边形,
$\because AD$是$\triangle ABC$的角平分线,
$\therefore\angle EAD=\angle FAD$,
$\because DE// AC$,
根据两直线平行,内错角相等,
$\therefore\angle EDA=\angle FAD$,
$\therefore\angle EAD=\angle EDA$,
根据等角对等边,
$\therefore AE = DE$,
根据一组邻边相等的平行四边形是菱形,
$\therefore$四边形$AEDF$是菱形。
【答案】:四边形$AEDF$是菱形。
证明:
$\because DE// AC,DF// AB$,
根据两组对边分别平行的四边形是平行四边形,
$\therefore$四边形$AEDF$是平行四边形,
$\because AD$是$\triangle ABC$的角平分线,
$\therefore\angle EAD=\angle FAD$,
$\because DE// AC$,
根据两直线平行,内错角相等,
$\therefore\angle EDA=\angle FAD$,
$\therefore\angle EAD=\angle EDA$,
根据等角对等边,
$\therefore AE = DE$,
根据一组邻边相等的平行四边形是菱形,
$\therefore$四边形$AEDF$是菱形。
【答案】:四边形$AEDF$是菱形。
查看更多完整答案,请扫码查看


