6. 如图所示,在$\triangle ABC$中,$AB = AC$,$AD⊥BC$,$M为AD$的中点,延长$CM交AB于点P$,$DN// CP交AB于点N$,若$AB = 6$,则$AP$的长为( )。

A.1
B.2.5
C.2
D.3

A.1
B.2.5
C.2
D.3
答案:
【解析】:因为在$\triangle ABC$中,$AB = AC$,$AD \perp BC$,根据等腰三角形三线合一的性质,所以$D$为$BC$的中点。
设$AP = x$,因为$AB = 6$,所以$PB = 6 - x$。
由于$DN // CP$,且$D$是$BC$的中点,根据平行线分线段成比例定理,可得$N$为$BP$的中点,因此$BN = NP = \frac{PB}{2} = \frac{6 - x}{2}$,那么$AN = AP + PN = x + \frac{6 - x}{2} = \frac{x + 6}{2}$。
又因为$M$是$AD$的中点,且$DN // PM$(因为$DN // CP$,$PM$是$CP$的一部分),所以在$\triangle ADN$中,$PM$是中位线,故$AP = PN$。
即$x = \frac{6 - x}{2}$,解方程可得:
$2x = 6 - x$
$3x = 6$
$x = 2$
所以$AP$的长为$2$。
【答案】:C
设$AP = x$,因为$AB = 6$,所以$PB = 6 - x$。
由于$DN // CP$,且$D$是$BC$的中点,根据平行线分线段成比例定理,可得$N$为$BP$的中点,因此$BN = NP = \frac{PB}{2} = \frac{6 - x}{2}$,那么$AN = AP + PN = x + \frac{6 - x}{2} = \frac{x + 6}{2}$。
又因为$M$是$AD$的中点,且$DN // PM$(因为$DN // CP$,$PM$是$CP$的一部分),所以在$\triangle ADN$中,$PM$是中位线,故$AP = PN$。
即$x = \frac{6 - x}{2}$,解方程可得:
$2x = 6 - x$
$3x = 6$
$x = 2$
所以$AP$的长为$2$。
【答案】:C
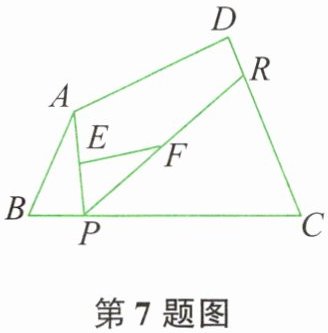
7. 如图所示,$R$、$P分别是四边形ABCD的边DC$、$BC$上的点,$E$、$F分别是AP$、$RP$的中点,当点$P在BC上从点B到点C移动而点R$不动时,下列结论正确的是( )。
A.线段$EF$的长逐渐增大
B.线段$EF$的长逐渐减小
C.线段$EF$的长不变
D.线段$EF$的长不能确定

A.线段$EF$的长逐渐增大
B.线段$EF$的长逐渐减小
C.线段$EF$的长不变
D.线段$EF$的长不能确定
答案:
【解析】:
因为$R$不动,所以$AR$长度不变。
根据三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半。
在$\triangle PAR$中,$E$、$F$分别是$AP$、$RP$的中点,所以$EF$是$\triangle PAR$的中位线,则$EF=\frac{1}{2}AR$。
由于$AR$长度不变,所以$EF$的长度也不变。
【答案】:C
因为$R$不动,所以$AR$长度不变。
根据三角形中位线定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半。
在$\triangle PAR$中,$E$、$F$分别是$AP$、$RP$的中点,所以$EF$是$\triangle PAR$的中位线,则$EF=\frac{1}{2}AR$。
由于$AR$长度不变,所以$EF$的长度也不变。
【答案】:C
8. 已知三角形的周长为24,则该三角形三条中位线的和为____。
答案:
【解析】:三角形的中位线平行于第三边,并且等于第三边的一半。设三角形的三条边分别为$a$、$b$、$c$,则三条中位线的长分别为$\frac{a}{2}$、$\frac{b}{2}$、$\frac{c}{2}$。已知三角形的周长为$24$,即$a + b + c = 24$,所以三条中位线的和为$\frac{a}{2} + \frac{b}{2} + \frac{c}{2} = \frac{a + b + c}{2} = \frac{24}{2} = 12$。
【答案】:12
【答案】:12
9. 直角三角形斜边上的中线长是6,则它的两条直角边中点的连线长是____。
答案:
【解析】:在直角三角形中,斜边上的中线等于斜边的一半。已知斜边上的中线长是6,所以斜边的长为$2×6 = 12$。
直角三角形两条直角边中点的连线是三角形的中位线,根据三角形中位线定理,三角形的中位线平行于第三边且等于第三边的一半。这里的第三边就是直角三角形的斜边,所以两条直角边中点的连线长等于斜边长度的一半,即$12÷2 = 6$。
【答案】:6
直角三角形两条直角边中点的连线是三角形的中位线,根据三角形中位线定理,三角形的中位线平行于第三边且等于第三边的一半。这里的第三边就是直角三角形的斜边,所以两条直角边中点的连线长等于斜边长度的一半,即$12÷2 = 6$。
【答案】:6
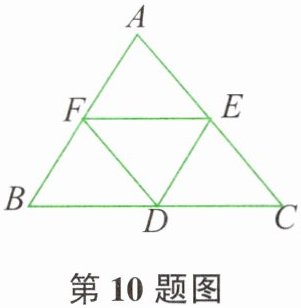
10. 如图所示,$D$、$E$、$F分别是\triangle ABC$中各边的中点,图中的平行四边形有____个;与$\triangle DEF$全等的三角形有____个;当$AB = AC$时,四边形$AEDF$是____形;当$∠A = 90^{\circ}$时,四边形$AEDF$是____形;当____时,四边形$AEDF$是正方形。

答案:
【解析】:
在$\triangle ABC$中,已知$D$、$E$、$F$分别是各边的中点,
根据中位线定理:三角形的中位线平行于第三边并且等于第三边边长的一半,
可得:$EF// AB$,$EF=\frac{1}{2}AB=AD=BD$;
$DE// AC$,$DE=\frac{1}{2}AC=AF=FC$;
$DF// BC$,$DF=\frac{1}{2}BC=BD=DC$。
由上述性质可得:
图中的平行四边形:
四边形$ADFE$、$BDEF$、$CDFE$都是平行四边形,共有$3$个。
与$\triangle DEF$全等的三角形:
由于$D$、$E$、$F$分别是各边的中点,
所以$\triangle DEF$的三条边分别平行且等于$\triangle ABC$三边的一半。
因此,与$\triangle DEF$全等的三角形有$\triangle BDF$和$\triangle CED$,共$2$个,
再加上$\triangle AEF$,共$3$个与$\triangle DEF$全等的三角形(因为这三个三角形都是由三角形的中位线构成的,它们都与$\triangle DEF$有相同的边长和角度)。
当$AB = AC$时:
由于$D$、$E$、$F$是中点,所以$AE = AF$,
又因为$EF// AB$,
所以四边形$AEDF$是菱形(四边相等且对边平行)。
当$\angle A = 90^{\circ}$时:
由于$EF// AB$,
所以$EF\perp AC$,
又因为$DE// AC$,
所以四边形$AEDF$是矩形(有一个角是直角的平行四边形是矩形,这里$EF// AB$且$DE// AC$,$\angle A = 90^{\circ}$,所以$AEDF$是矩形)。
当$AB = AC$且$\angle A = 90^{\circ}$时:
结合前面的分析,四边形$AEDF$既是菱形又是矩形,
所以它是正方形(一组邻边相等的矩形是菱形,有一个角是直角的菱形是矩形,既是矩形又是菱形的四边形是正方形)。
【答案】:
3;3;菱;矩;$AB = AC$且$\angle A = 90^{\circ}$。
在$\triangle ABC$中,已知$D$、$E$、$F$分别是各边的中点,
根据中位线定理:三角形的中位线平行于第三边并且等于第三边边长的一半,
可得:$EF// AB$,$EF=\frac{1}{2}AB=AD=BD$;
$DE// AC$,$DE=\frac{1}{2}AC=AF=FC$;
$DF// BC$,$DF=\frac{1}{2}BC=BD=DC$。
由上述性质可得:
图中的平行四边形:
四边形$ADFE$、$BDEF$、$CDFE$都是平行四边形,共有$3$个。
与$\triangle DEF$全等的三角形:
由于$D$、$E$、$F$分别是各边的中点,
所以$\triangle DEF$的三条边分别平行且等于$\triangle ABC$三边的一半。
因此,与$\triangle DEF$全等的三角形有$\triangle BDF$和$\triangle CED$,共$2$个,
再加上$\triangle AEF$,共$3$个与$\triangle DEF$全等的三角形(因为这三个三角形都是由三角形的中位线构成的,它们都与$\triangle DEF$有相同的边长和角度)。
当$AB = AC$时:
由于$D$、$E$、$F$是中点,所以$AE = AF$,
又因为$EF// AB$,
所以四边形$AEDF$是菱形(四边相等且对边平行)。
当$\angle A = 90^{\circ}$时:
由于$EF// AB$,
所以$EF\perp AC$,
又因为$DE// AC$,
所以四边形$AEDF$是矩形(有一个角是直角的平行四边形是矩形,这里$EF// AB$且$DE// AC$,$\angle A = 90^{\circ}$,所以$AEDF$是矩形)。
当$AB = AC$且$\angle A = 90^{\circ}$时:
结合前面的分析,四边形$AEDF$既是菱形又是矩形,
所以它是正方形(一组邻边相等的矩形是菱形,有一个角是直角的菱形是矩形,既是矩形又是菱形的四边形是正方形)。
【答案】:
3;3;菱;矩;$AB = AC$且$\angle A = 90^{\circ}$。
11. 如图所示,$P为□ ABCD边AD$上一点,$E$、$F分别为PB$、$PC$的中点,$\triangle PEF$、$\triangle PDC$、$\triangle PAB的面积分别为S$、$S_{1}$、$S_{2}$。若$S = 2$,则$S_{1} + S_{2} = $____。


答案:
【解析】:在平行四边形 $ABCD$ 中,$P$ 是边 $AD$ 上一点。$E$、$F$ 分别为 $PB$、$PC$ 的中点,所以 $EF$ 是 $\triangle PBC$ 的中位线。根据中位线性质,$EF // BC$ 且 $EF = \frac{1}{2}BC$。
$\triangle PEF$ 与 $\triangle PBC$ 相似,相似比为 $\frac{1}{2}$,因此面积比为 $(\frac{1}{2})^2 = \frac{1}{4}$。已知 $S_{\triangle PEF} = S = 2$,则 $S_{\triangle PBC} = 4S = 4 × 2 = 8$。
因为平行四边形 $ABCD$ 的面积等于 $\triangle PAB$、$\triangle PDC$ 和 $\triangle PBC$ 的面积之和,且 $\triangle PAB$ 与 $\triangle PDC$ 的面积之和等于平行四边形面积减去 $\triangle PBC$ 的面积。又因为平行四边形中,$\triangle PBC$ 的面积是平行四边形面积的一半(以 $BC$ 为底,高与平行四边形相同),所以 $S_1 + S_2 = S_{\triangle PBC} = 8$。
【答案】:8
$\triangle PEF$ 与 $\triangle PBC$ 相似,相似比为 $\frac{1}{2}$,因此面积比为 $(\frac{1}{2})^2 = \frac{1}{4}$。已知 $S_{\triangle PEF} = S = 2$,则 $S_{\triangle PBC} = 4S = 4 × 2 = 8$。
因为平行四边形 $ABCD$ 的面积等于 $\triangle PAB$、$\triangle PDC$ 和 $\triangle PBC$ 的面积之和,且 $\triangle PAB$ 与 $\triangle PDC$ 的面积之和等于平行四边形面积减去 $\triangle PBC$ 的面积。又因为平行四边形中,$\triangle PBC$ 的面积是平行四边形面积的一半(以 $BC$ 为底,高与平行四边形相同),所以 $S_1 + S_2 = S_{\triangle PBC} = 8$。
【答案】:8
查看更多完整答案,请扫码查看


