6. 在$□ ABCD$中,$\angle B= 70^{\circ}$,则$\angle A$的度数为( )。
A.$50^{\circ}$
B.$80^{\circ}$
C.$110^{\circ}$
D.$140^{\circ}$
A.$50^{\circ}$
B.$80^{\circ}$
C.$110^{\circ}$
D.$140^{\circ}$
答案:
【解析】:在平行四边形中,对角是相等的,且相邻两角之和为$180^{\circ}$。
已知$\angle B = 70^{\circ}$,由于$ABCD$是平行四边形,根据平行四边形的性质,我们有$\angle A + \angle B = 180^{\circ}$。
因此,$\angle A = 180^{\circ} - \angle B = 180^{\circ} - 70^{\circ} = 110^{\circ}$。
【答案】:$110^{\circ}$
已知$\angle B = 70^{\circ}$,由于$ABCD$是平行四边形,根据平行四边形的性质,我们有$\angle A + \angle B = 180^{\circ}$。
因此,$\angle A = 180^{\circ} - \angle B = 180^{\circ} - 70^{\circ} = 110^{\circ}$。
【答案】:$110^{\circ}$
7. 如图所示,在$□ ABCD$中,$\angle ACB= \angle B= 50^{\circ}$,则$\angle ACD= $______。


答案:
【解析】:在平行四边形$ABCD$中,$AD// BC$,$AB// CD$,所以$\angle B + \angle BCD = 180^{\circ}$(两直线平行,同旁内角互补)。已知$\angle B = 50^{\circ}$,则$\angle BCD=180^{\circ}-\angle B = 180^{\circ}-50^{\circ}=130^{\circ}$。
又因为$\angle ACB = 50^{\circ}$,且$\angle BCD=\angle ACB+\angle ACD$,所以$\angle ACD=\angle BCD - \angle ACB=130^{\circ}-50^{\circ}=80^{\circ}$。
【答案】:80°
又因为$\angle ACB = 50^{\circ}$,且$\angle BCD=\angle ACB+\angle ACD$,所以$\angle ACD=\angle BCD - \angle ACB=130^{\circ}-50^{\circ}=80^{\circ}$。
【答案】:80°
8. 如图所示,等腰三角形$\triangle ABC的一腰AB= 4cm$,过底边$BC上的任一点D$作两腰的平行线,分别交两腰于$E$、$F$,则$□ AEDF$的周长是______。


答案:
【解析】:
1. $\triangle ABC$是等腰三角形,$AB = AC = 4 \text{cm}$。
2. $E$和$F$分别是$AB$和$AC$上的点,并且$DE // AC$,$DF // AB$,所以四边形$AEDF$是平行四边形。
3. 因为$DE // AC$,所以$\angle BDE = \angle C$,又因为$\triangle ABC$是等腰三角形,所以$\angle B = \angle C$,所以$\angle B = \angle BDE$,因此$\triangle BDE$是等腰三角形,$BE = DE$。
4. 同理,$\triangle CDF$也是等腰三角形,$CF = DF$。
5. 因为$AEDF$是平行四边形,所以$DE = AF$,$AE = DF$。
6. 平行四边形$AEDF$的周长为:
$AE + ED + DF + FA = AE + BE + CF + AF = AB + AC = 4 \text{cm} + 4 \text{cm} = 8 \text{cm}$。
【答案】:8cm
1. $\triangle ABC$是等腰三角形,$AB = AC = 4 \text{cm}$。
2. $E$和$F$分别是$AB$和$AC$上的点,并且$DE // AC$,$DF // AB$,所以四边形$AEDF$是平行四边形。
3. 因为$DE // AC$,所以$\angle BDE = \angle C$,又因为$\triangle ABC$是等腰三角形,所以$\angle B = \angle C$,所以$\angle B = \angle BDE$,因此$\triangle BDE$是等腰三角形,$BE = DE$。
4. 同理,$\triangle CDF$也是等腰三角形,$CF = DF$。
5. 因为$AEDF$是平行四边形,所以$DE = AF$,$AE = DF$。
6. 平行四边形$AEDF$的周长为:
$AE + ED + DF + FA = AE + BE + CF + AF = AB + AC = 4 \text{cm} + 4 \text{cm} = 8 \text{cm}$。
【答案】:8cm
9. 如图所示,在$□ ABCD$中,$AB= 4cm$,$AD= 7cm$,$\angle ABC的平分线交AD于点E$,交$CD的延长线于点F$,则$DF= $______。


答案:
【解析】:在平行四边形$ABCD$中,$AB// CD$,$AD// BC$,$AB = CD = 4\space cm$,$AD = BC = 7\space cm$。
因为$BF$是$\angle ABC$的平分线,所以$\angle ABE=\angle CBE$。
由于$AD// BC$,根据两直线平行内错角相等,可得$\angle AEB = \angle CBE$,因此$\angle ABE=\angle AEB$,所以$\triangle ABE$是等腰三角形,$AE = AB = 4\space cm$。
则$DE=AD - AE=7 - 4=3\space cm$。
又因为$AB// CD$,所以$\angle F=\angle ABE$(两直线平行内错角相等),且$\angle AEB=\angle FED$(对顶角相等),而$\angle ABE=\angle AEB$,故$\angle F=\angle FED$,所以$\triangle FED$是等腰三角形,$DF = DE = 3\space cm$。
【答案】:3
因为$BF$是$\angle ABC$的平分线,所以$\angle ABE=\angle CBE$。
由于$AD// BC$,根据两直线平行内错角相等,可得$\angle AEB = \angle CBE$,因此$\angle ABE=\angle AEB$,所以$\triangle ABE$是等腰三角形,$AE = AB = 4\space cm$。
则$DE=AD - AE=7 - 4=3\space cm$。
又因为$AB// CD$,所以$\angle F=\angle ABE$(两直线平行内错角相等),且$\angle AEB=\angle FED$(对顶角相等),而$\angle ABE=\angle AEB$,故$\angle F=\angle FED$,所以$\triangle FED$是等腰三角形,$DF = DE = 3\space cm$。
【答案】:3
10. 如图所示,在$□ ABCD$中,$\angle ABD= 90^{\circ}$,若$AB= 3$,$BC= 5$,则$□ ABCD$的面积为______。
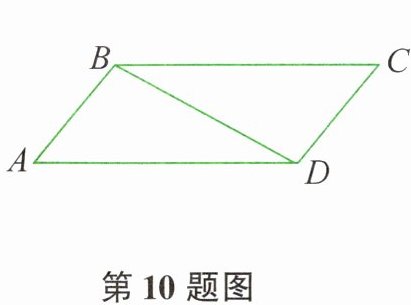

答案:
【解析】:
因为四边形$ABCD$是平行四边形,
根据平行四边形对边相等的性质可得:$AB=CD=3$,$BC=AD=5$。
在$\triangle ABD$中,$\angle ABD=90^{\circ}$,$AB = 3$,$AD = 5$,
根据勾股定理:在任何一个直角三角形中,两条直角边长的平方和等于斜边长的平方。
可得:$BD=\sqrt{AD^{2}-AB^{2}}=\sqrt{5^{2}-3^{2}}=\sqrt{25 - 9}=\sqrt{16}=4$。
平行四边形的面积可以看作是两个全等的三角形面积之和,
这里可以把$□ ABCD$看作是由$\triangle ABD$和$\triangle BCD$组成,
$\triangle ABD$以$AB$为底时,$BD$为高,
根据三角形面积公式$S=\frac{1}{2}×底×高$,
可得$S_{\triangle ABD}=\frac{1}{2}× AB× BD=\frac{1}{2}×3×4 = 6$。
那么平行四边形$ABCD$的面积$S = 2S_{\triangle ABD}=AB× BD=3×4 = 12$。
【答案】:12
因为四边形$ABCD$是平行四边形,
根据平行四边形对边相等的性质可得:$AB=CD=3$,$BC=AD=5$。
在$\triangle ABD$中,$\angle ABD=90^{\circ}$,$AB = 3$,$AD = 5$,
根据勾股定理:在任何一个直角三角形中,两条直角边长的平方和等于斜边长的平方。
可得:$BD=\sqrt{AD^{2}-AB^{2}}=\sqrt{5^{2}-3^{2}}=\sqrt{25 - 9}=\sqrt{16}=4$。
平行四边形的面积可以看作是两个全等的三角形面积之和,
这里可以把$□ ABCD$看作是由$\triangle ABD$和$\triangle BCD$组成,
$\triangle ABD$以$AB$为底时,$BD$为高,
根据三角形面积公式$S=\frac{1}{2}×底×高$,
可得$S_{\triangle ABD}=\frac{1}{2}× AB× BD=\frac{1}{2}×3×4 = 6$。
那么平行四边形$ABCD$的面积$S = 2S_{\triangle ABD}=AB× BD=3×4 = 12$。
【答案】:12
查看更多完整答案,请扫码查看


