13. 某市出租车计费方法如图所示,$x(km)$表示行驶里程,$y$(元)表示车费,请根据图像回答下面的问题。
(1)出租车的起步价是多少元?当$x > 3$时,求$y关于x$的函数解析式。
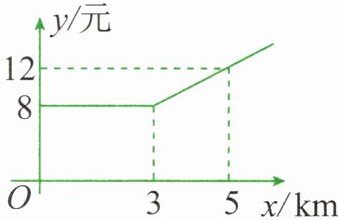
(2)若某乘客有一次乘出租车的车费为$32$元,求这位乘客乘车的里程。
(1)出租车的起步价是多少元?当$x > 3$时,求$y关于x$的函数解析式。

(2)若某乘客有一次乘出租车的车费为$32$元,求这位乘客乘车的里程。
答案:
【解析】:
(1) 由图像可知,出租车的起步价为8元(即当$x=0$到$x=3$时,$y=8$)。
当$x>3$时,设$y$关于$x$的函数解析式为$y=kx+b$,
因为图像过点$(3,8)$和$(5,12)$,
将这两点代入$y=kx+b$,
可得方程组:
$\begin{cases}3k+b=8 \\5k+b=12\end{cases}$
用第二个方程减去第一个方程消去$b$:
$(5k+b)-(3k+b)=12-8$
$2k=4$
$k=2$
将$k=2$代入$3k+b=8$,
$3×2+b=8$
$b=2$
所以,当$x>3$时,$y$关于$x$的函数解析式为$y=2x+2$。
(2) 已知车费$y=32$元,因为起步价8元对应$x\leq3$,而32元大于8元,所以$x>3$,
将$y=32$代入$y=2x+2$,
$32=2x+2$
$2x=30$
$x=15$
【答案】:
(1) 出租车的起步价是8元;当$x>3$时,$y$关于$x$的函数解析式为$y=2x+2$。
(2) 这位乘客乘车的里程为15km。
(1) 由图像可知,出租车的起步价为8元(即当$x=0$到$x=3$时,$y=8$)。
当$x>3$时,设$y$关于$x$的函数解析式为$y=kx+b$,
因为图像过点$(3,8)$和$(5,12)$,
将这两点代入$y=kx+b$,
可得方程组:
$\begin{cases}3k+b=8 \\5k+b=12\end{cases}$
用第二个方程减去第一个方程消去$b$:
$(5k+b)-(3k+b)=12-8$
$2k=4$
$k=2$
将$k=2$代入$3k+b=8$,
$3×2+b=8$
$b=2$
所以,当$x>3$时,$y$关于$x$的函数解析式为$y=2x+2$。
(2) 已知车费$y=32$元,因为起步价8元对应$x\leq3$,而32元大于8元,所以$x>3$,
将$y=32$代入$y=2x+2$,
$32=2x+2$
$2x=30$
$x=15$
【答案】:
(1) 出租车的起步价是8元;当$x>3$时,$y$关于$x$的函数解析式为$y=2x+2$。
(2) 这位乘客乘车的里程为15km。
1. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为$y_{1}(km)$,出租车离甲地的距离为$y_{2}(km)$,两车行驶的时间为$x(h)$,$y_{1}$、$y_{2}关于x$的函数图像如下页图所示。
(1)根据图像,直接写出$y_{1}$、$y_{2}关于x$的函数关系式;
(2)若两车之间的距离为$S km$,请写出$S关于x$的函数关系式;
(3)甲、乙两地间有$A$、$B$两个加油站,相距$200km$,若客车进入$A$加油站时,出租车恰好进入$B$加油站,求$A$加油站与甲地的距离。
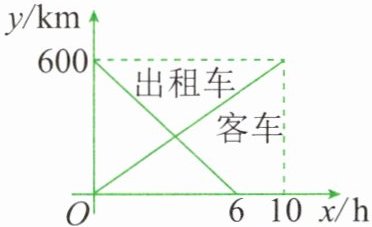
(1)根据图像,直接写出$y_{1}$、$y_{2}关于x$的函数关系式;
(2)若两车之间的距离为$S km$,请写出$S关于x$的函数关系式;
(3)甲、乙两地间有$A$、$B$两个加油站,相距$200km$,若客车进入$A$加油站时,出租车恰好进入$B$加油站,求$A$加油站与甲地的距离。

答案:
【解析】:
(1)根据图像和题意,可以确定两车的运动方式为匀速直线运动。
客车的图像是一条从原点出发的直线,到点$(10, 600)$结束,
因此客车的速度为$600 ÷ 10 = 60(km/h)$,
所以$y_1 = 60x$。
出租车的图像是一条从$(0, 600)$出发的直线,到点$(6, 0)$结束,
因此出租车的速度为$(600-0) ÷ 6 = 100(km/h)$,
但因为是向甲地行驶,所以距离甲地的距离在减少,
用$600$减去行驶的距离就是离甲地的距离,
即$y_2 = 600 - 100x$。
所以$y_1$、$y_2$关于$x$的函数关系式分别为:
$y_1 = 60x$,$y_2 = 600 - 100x$。
(2)两车之间的距离$S$为客车离甲地的距离$y_1$与出租车离甲地的距离$y_2$之差的绝对值,
即$S = |y_1 - y_2| = |60x - (600 - 100x)| = |160x - 600|$。
根据$x$的取值范围,可以得到$S$的分段函数关系式:
当$0 \leq x \leq \frac{15}{4}$时,$S = 600 - 160x$;
当$\frac{15}{4} < x < 6$时,$S = 160x - 600$;
当$6 \leq x \leq 10$时,$S = 60x$。
所以$S$关于$x$的函数关系式为:
$S = \begin{cases}600 - 160x,0 \leq x \leq \frac{15}{4}, \\160x - 600, \frac{15}{4} < x < 6, \\60x.6 \leq x \leq 10.\end{cases}$
(3)设$A$加油站与甲地的距离为$y_A km$,行驶的时间为$x h$。
当$0 \leq x \leq \frac{15}{4}$时,
$y_A = 60x$,
$y_B=600-100x$,
$y_A+200=y_B$,
则$60x+200=600-100x$,
$160x=400$,
$x=\frac{5}{2}$,
$y_A = 60 × \frac{5}{2}=150$;
当$\frac{15}{4} < x < 6$时,
$y_A = 60x$,
$y_B=600-100x$,
$y_A=200+y_B$,
则$60x=200+600-100x$,
$160x=800$,
$x=5$,
$y_A = 60 × 5=300$;
$A$加油站离甲地距离为$150km$或$300km$。
【答案】:
(1)$y_1 = 60x$,$y_2 = 600 - 100x$;
(2)$S = \begin{cases}600 - 160x,0 \leq x \leq \frac{15}{4}, \\160x - 600, \frac{15}{4} < x < 6, \\60x.6 \leq x \leq 10.\end{cases}$
(3)$A$加油站离甲地距离为$150km$或$300km$。
(1)根据图像和题意,可以确定两车的运动方式为匀速直线运动。
客车的图像是一条从原点出发的直线,到点$(10, 600)$结束,
因此客车的速度为$600 ÷ 10 = 60(km/h)$,
所以$y_1 = 60x$。
出租车的图像是一条从$(0, 600)$出发的直线,到点$(6, 0)$结束,
因此出租车的速度为$(600-0) ÷ 6 = 100(km/h)$,
但因为是向甲地行驶,所以距离甲地的距离在减少,
用$600$减去行驶的距离就是离甲地的距离,
即$y_2 = 600 - 100x$。
所以$y_1$、$y_2$关于$x$的函数关系式分别为:
$y_1 = 60x$,$y_2 = 600 - 100x$。
(2)两车之间的距离$S$为客车离甲地的距离$y_1$与出租车离甲地的距离$y_2$之差的绝对值,
即$S = |y_1 - y_2| = |60x - (600 - 100x)| = |160x - 600|$。
根据$x$的取值范围,可以得到$S$的分段函数关系式:
当$0 \leq x \leq \frac{15}{4}$时,$S = 600 - 160x$;
当$\frac{15}{4} < x < 6$时,$S = 160x - 600$;
当$6 \leq x \leq 10$时,$S = 60x$。
所以$S$关于$x$的函数关系式为:
$S = \begin{cases}600 - 160x,0 \leq x \leq \frac{15}{4}, \\160x - 600, \frac{15}{4} < x < 6, \\60x.6 \leq x \leq 10.\end{cases}$
(3)设$A$加油站与甲地的距离为$y_A km$,行驶的时间为$x h$。
当$0 \leq x \leq \frac{15}{4}$时,
$y_A = 60x$,
$y_B=600-100x$,
$y_A+200=y_B$,
则$60x+200=600-100x$,
$160x=400$,
$x=\frac{5}{2}$,
$y_A = 60 × \frac{5}{2}=150$;
当$\frac{15}{4} < x < 6$时,
$y_A = 60x$,
$y_B=600-100x$,
$y_A=200+y_B$,
则$60x=200+600-100x$,
$160x=800$,
$x=5$,
$y_A = 60 × 5=300$;
$A$加油站离甲地距离为$150km$或$300km$。
【答案】:
(1)$y_1 = 60x$,$y_2 = 600 - 100x$;
(2)$S = \begin{cases}600 - 160x,0 \leq x \leq \frac{15}{4}, \\160x - 600, \frac{15}{4} < x < 6, \\60x.6 \leq x \leq 10.\end{cases}$
(3)$A$加油站离甲地距离为$150km$或$300km$。
查看更多完整答案,请扫码查看


