《2025年暑假作业八年级数学人教版教育科学出版社》

1. 如果平行四边形有一组对角互补,那么这个平行四边形的四个角一定都是( )。

A.直角
B.钝角
C.锐角
D.不确定

答案： 【解析】：在平行四边形中，对角相等，邻角互补。已知一组对角互补，设这组对角分别为∠A和∠C，因为∠A=∠C，且∠A+∠C=180°，所以∠A=∠C=90°。又因为邻角互补，所以∠B=180°-∠A=90°，∠D=180°-∠C=90°，因此四个角都是直角。
【答案】：A

2. 下列条件中,能判定四边形是平行四边形的条件是( )。

A.两条对角线互相垂直
B.两条对角线互相垂直且相等
C.两条对角线相等且交角为$60^{\circ}$
D.两条对角线互相平分

答案： 【解析】：根据平行四边形的判定定理，对角线互相平分的四边形是平行四边形。选项A中两条对角线互相垂直，可能是菱形或筝形等，不一定是平行四边形；选项B两条对角线互相垂直且相等，可能是正方形或等腰梯形等，不一定是平行四边形；选项C两条对角线相等且交角为60°，无法直接判定为平行四边形；选项D两条对角线互相平分，符合平行四边形的判定条件。
【答案】：D

3. 如图所示,在$□ ABCD$中,$∠B - ∠A = 20^{\circ}$,则$∠D$的度数是( )。


A.$80^{\circ}$

B.$90^{\circ}$
C.$100^{\circ}$
D.$110^{\circ}$

答案： 【解析】：
在平行四边形$ABCD$中，$\angle A$和$\angle B$是相邻内角，故$\angle A + \angle B = 180^\circ$。
已知$\angle B - \angle A = 20^\circ$，
联立方程：
$\begin{cases}\angle A + \angle B = 180^\circ, \\\angle B - \angle A = 20^\circ.\end{cases}$
将两个方程相加：
$2\angle B = 200^\circ \implies \angle B = 100^\circ$。
将$\angle B = 100^\circ$代入$\angle A + \angle B = 180^\circ$：
$\angle A + 100^\circ = 180^\circ \implies \angle A = 80^\circ$。
在平行四边形中，对角相等，故$\angle D = \angle B = 100^\circ$。
【答案】：C.$100^\circ$

4. 如图所示,$AC$、$BD是□ ABCD$的对角线,$AC和BD相交于点O$,$AC = 4$,$BD = 5$,$BC = 3$,则$\triangle BOC$的周长是( )。


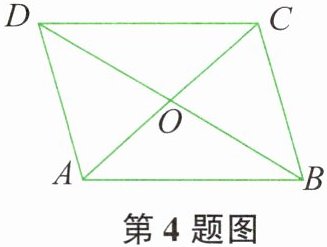
A.7.5
B.12
C.8.5
D.9

答案： 【解析】：
在平行四边形$ABCD$中，对角线$AC$和$BD$相交于点$O$，根据平行四边形的性质，对角线互相平分。
已知$AC = 4$，$BD = 5$，$BC = 3$。
所以$OC=\frac{1}{2}AC = 2$，$OB=\frac{1}{2}BD = 2.5$。
$\triangle BOC$的周长为$BC + OB + OC$，将数值代入可得：
$3 + 2.5 + 2 = 7.5$。
【答案】：A

5. 已知$\triangle ABC$的周长为1,连接$\triangle ABC$三边的中点构成第2个三角形,再连接第2个三角形三边的中点构成第3个三角形,依此类推,第2015个三角形的周长是( )。

A.$\frac{1}{2014}$
B.$\frac{1}{2015}$
C.$\frac{1}{2^{2014}}$
D.$\frac{1}{2^{2015}}$

答案： 【解析】：连接三角形三边中点构成的新三角形，其周长是原三角形周长的一半。第一个三角形（原三角形）周长为1，第2个三角形周长为$1×\frac{1}{2}=\frac{1}{2^1}$，第3个三角形周长为$\frac{1}{2}×\frac{1}{2}=\frac{1}{2^2}$，依此类推，第n个三角形的周长为$\frac{1}{2^{n-1}}$。当n=2015时，周长为$\frac{1}{2^{2015-1}}=\frac{1}{2^{2014}}$。
【答案】：C