17. 在 $ \mathrm { Rt } \triangle A B C $中,$ \angle C = 90 ^ { \circ } $,若 $ a : b = 3 : 4 $,$ c = 10 $,则 $ S _ { \mathrm { Rt } \triangle A B C } = $____。
答案:
【解析】:
在直角三角形 $ \triangle ABC $ 中,已知 $ \angle C = 90^\circ $,且 $ a : b = 3 : 4 $,斜边 $ c = 10 $。
设 $ a = 3k $,$ b = 4k $,其中 $ k $ 为比例系数。
根据勾股定理:
$a^2 + b^2 = c^2$,
代入已知条件:
$(3k)^2 + (4k)^2 = 10^2$,
$9k^2 + 16k^2 = 100$,
$25k^2 = 100$,
$k^2 = 4$,
$k = 2$,
因此,$ a = 3k = 6 $,$ b = 4k = 8 $。
直角三角形的面积为:
$S_{\triangle ABC} = \frac{1}{2} × a × b = \frac{1}{2} × 6 × 8 = 24$。
【答案】:24
在直角三角形 $ \triangle ABC $ 中,已知 $ \angle C = 90^\circ $,且 $ a : b = 3 : 4 $,斜边 $ c = 10 $。
设 $ a = 3k $,$ b = 4k $,其中 $ k $ 为比例系数。
根据勾股定理:
$a^2 + b^2 = c^2$,
代入已知条件:
$(3k)^2 + (4k)^2 = 10^2$,
$9k^2 + 16k^2 = 100$,
$25k^2 = 100$,
$k^2 = 4$,
$k = 2$,
因此,$ a = 3k = 6 $,$ b = 4k = 8 $。
直角三角形的面积为:
$S_{\triangle ABC} = \frac{1}{2} × a × b = \frac{1}{2} × 6 × 8 = 24$。
【答案】:24
18. 直角三角形两直角边边长分别为 5 和 12,则它斜边上的高为____。
答案:
【解析】:
首先,根据勾股定理,直角三角形的斜边长度 $c$ 可以计算为:
$c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13$,
设斜边上的高为 $h$,根据直角三角形的面积公式,面积 $S$ 可以用两种方式表示:
一是基于两直角边的长度:$S = \frac{1}{2} × 5 × 12 = 30$,
二是基于斜边和斜边上的高:$S = \frac{1}{2} × 13 × h$,
由于两种方式表示的面积必须相等,有:
$\frac{1}{2} × 13 × h = 30$,
解这个方程,得到:
$h = \frac{60}{13}$。
【答案】:$\frac{60}{13}$。
首先,根据勾股定理,直角三角形的斜边长度 $c$ 可以计算为:
$c = \sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13$,
设斜边上的高为 $h$,根据直角三角形的面积公式,面积 $S$ 可以用两种方式表示:
一是基于两直角边的长度:$S = \frac{1}{2} × 5 × 12 = 30$,
二是基于斜边和斜边上的高:$S = \frac{1}{2} × 13 × h$,
由于两种方式表示的面积必须相等,有:
$\frac{1}{2} × 13 × h = 30$,
解这个方程,得到:
$h = \frac{60}{13}$。
【答案】:$\frac{60}{13}$。
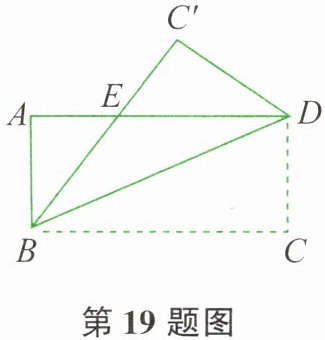
19. 如图所示,矩形 ABCD 沿着直线 BD 折叠,使点 C 落在 $ C ^ { \prime } $处,$ B C ^ { \prime } $交 AD 于点 E,$ A D = 8 $,$ A B = 4 $,则 DE 的长为____。

答案:
【解析】:
设 $ DE = x $,则 $ AE = 8 - x $。
因为矩形 $ ABCD $ 沿着直线 $ BD $ 折叠,使点 $ C $ 落在 $ C' $ 处,
所以 $\angle EBD = \angle CBD $。
因为 $ AD // BC $,
所以$\angle CBD = \angle EDB $。
所以$\angle EBD = \angle EDB $。
所以$ BE = DE = x $。
在直角三角形 $ ABE $ 中,根据勾股定理:
$ BE^2 = AB^2 + AE^2 $。
即$ x^2 = 4^2 + (8 - x)^2 $。
展开并简化方程:
$ x^2 = 16 + 64 - 16x + x^2 $。
$ 16x = 80 $。
$ x = 5 $。
【答案】:5
设 $ DE = x $,则 $ AE = 8 - x $。
因为矩形 $ ABCD $ 沿着直线 $ BD $ 折叠,使点 $ C $ 落在 $ C' $ 处,
所以 $\angle EBD = \angle CBD $。
因为 $ AD // BC $,
所以$\angle CBD = \angle EDB $。
所以$\angle EBD = \angle EDB $。
所以$ BE = DE = x $。
在直角三角形 $ ABE $ 中,根据勾股定理:
$ BE^2 = AB^2 + AE^2 $。
即$ x^2 = 4^2 + (8 - x)^2 $。
展开并简化方程:
$ x^2 = 16 + 64 - 16x + x^2 $。
$ 16x = 80 $。
$ x = 5 $。
【答案】:5
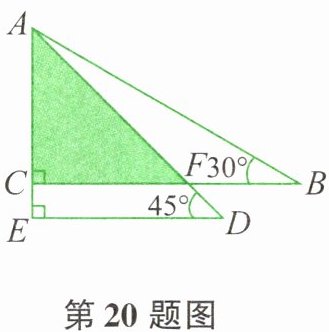
20. 将一副三角尺如图所示叠放在一起,若 $ A B = 14 \mathrm { cm } $,则阴影部分的面积是____$ \mathrm { cm } ^ { 2 } $。

答案:
【解析】:
由于 $ \angle B = 30^\circ $, $ \angle ACB = 90^\circ $, $ AB = 14 $ cm,
所以 $ AC = 7 $ cm。
又因为 $ \angle F = 45^\circ $, $ \angle ACB = 90^\circ $,
所以 $ \angle CAF = 45^\circ $。
因此三角形 $ \triangle ACF $ 是等腰直角三角形,
即 $ AC = CF = 7 $ cm。
阴影部分的面积为:
$\frac{1}{2} × 7 × 7 = \frac{49}{2} = 24.5 $($\mathrm{cm}^2$)。
【答案】:24.5
由于 $ \angle B = 30^\circ $, $ \angle ACB = 90^\circ $, $ AB = 14 $ cm,
所以 $ AC = 7 $ cm。
又因为 $ \angle F = 45^\circ $, $ \angle ACB = 90^\circ $,
所以 $ \angle CAF = 45^\circ $。
因此三角形 $ \triangle ACF $ 是等腰直角三角形,
即 $ AC = CF = 7 $ cm。
阴影部分的面积为:
$\frac{1}{2} × 7 × 7 = \frac{49}{2} = 24.5 $($\mathrm{cm}^2$)。
【答案】:24.5
21. 在平静的湖面上,有一枝红莲,高出水面 1m。一阵风吹来,红莲被吹到一边,花朵齐及水面。已知红莲摆动的水平距离为 2m,问这里的水深是____m。
答案:
【解析】:
设水深为 $h$ 米。
红莲高出水面1米,所以红莲的总长度为 $h+1$ 米。
当红莲被吹到一边,花朵齐及水面,此时红莲、水深和红莲摆动的水平距离构成一个直角三角形。
在这个直角三角形中,红莲的总长度 $h+1$ 是斜边,水深 $h$ 和红莲摆动的水平距离2米是两直角边。
根据勾股定理,有:
$h^2 + 2^2 = (h+1)^2$
$h^2 + 4 = h^2 + 2h + 1$
$4 = 2h + 1$
$2h = 3$
$h = 1.5$
所以,这里的水深是1.5米。
【答案】:1.5
设水深为 $h$ 米。
红莲高出水面1米,所以红莲的总长度为 $h+1$ 米。
当红莲被吹到一边,花朵齐及水面,此时红莲、水深和红莲摆动的水平距离构成一个直角三角形。
在这个直角三角形中,红莲的总长度 $h+1$ 是斜边,水深 $h$ 和红莲摆动的水平距离2米是两直角边。
根据勾股定理,有:
$h^2 + 2^2 = (h+1)^2$
$h^2 + 4 = h^2 + 2h + 1$
$4 = 2h + 1$
$2h = 3$
$h = 1.5$
所以,这里的水深是1.5米。
【答案】:1.5
22. 已知两条线段的长为 5cm 和 12cm,当第三条线段的长为____cm 时,这三条线段能组成一个直角三角形。
答案:
【解析】:已知两条线段的长为 5cm 和 12cm,要使这三条线段能组成一个直角三角形,需分两种情况讨论:
1. 当 5cm 和 12cm 为直角边时,根据勾股定理,第三条线段(斜边)的长为:$\sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13$cm。
2. 当 12cm 为斜边,5cm 为直角边时,第三条线段(另一条直角边)的长为:$\sqrt{12^2 - 5^2} = \sqrt{144 - 25} = \sqrt{119}$cm。
综上,第三条线段的长为 13 或$\sqrt{119}$cm。
【答案】:13 或$\sqrt{119}$
1. 当 5cm 和 12cm 为直角边时,根据勾股定理,第三条线段(斜边)的长为:$\sqrt{5^2 + 12^2} = \sqrt{25 + 144} = \sqrt{169} = 13$cm。
2. 当 12cm 为斜边,5cm 为直角边时,第三条线段(另一条直角边)的长为:$\sqrt{12^2 - 5^2} = \sqrt{144 - 25} = \sqrt{119}$cm。
综上,第三条线段的长为 13 或$\sqrt{119}$cm。
【答案】:13 或$\sqrt{119}$
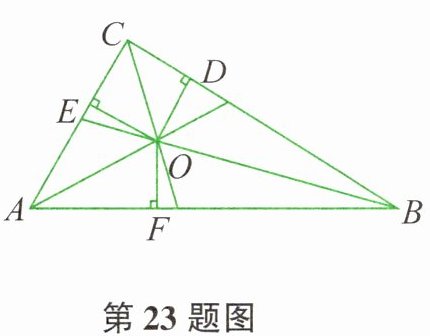
23. 如图所示,在 $ \triangle A B C $中,$ \angle C = 90 ^ { \circ } $,点 O 为 $ \triangle A B C $的三条角平分线的交点,$ O D \perp B C $,$ O E \perp A C $,$ O F \perp A B $,点 D、E、F 分别是垂足,且 $ B C = 8 \mathrm { cm } $,$ C A = 6 \mathrm { cm } $,则点 O 到三边 AB、AC 和 BC 的距离分别等于____cm、____cm 及____cm。

答案:
【解析】:在直角三角形 $ \triangle ABC $ 中,$ \angle C = 90^\circ $,$ BC = 8 \, \text{cm} $,$ CA = 6 \, \text{cm} $。根据勾股定理,$ AB = \sqrt{AC^2 + BC^2} = \sqrt{6^2 + 8^2} = 10 \, \text{cm} $。
点 $ O $ 是 $ \triangle ABC $ 三条角平分线的交点,即内心。内心到三角形三边的距离相等,设该距离为 $ r $。
直角三角形的面积可表示为两直角边乘积的一半,即 $ S_{\triangle ABC} = \frac{1}{2} × AC × BC = \frac{1}{2} × 6 × 8 = 24 \, \text{cm}^2 $。
同时,三角形面积也可表示为三个小三角形 $ \triangle AOB $、$ \triangle BOC $、$ \triangle AOC $ 面积之和,即:
$S_{\triangle ABC} = \frac{1}{2} × AB × r + \frac{1}{2} × BC × r + \frac{1}{2} × AC × r = \frac{1}{2} × (AB + BC + AC) × r$
代入已知值:
$24 = \frac{1}{2} × (10 + 8 + 6) × r$
解得:
$24 = \frac{1}{2} × 24 × r \implies 24 = 12r \implies r = 2$
因此,点 $ O $ 到三边 $ AB $、$ AC $、$ BC $ 的距离均为 $ 2 \, \text{cm} $。
【答案】:2,2,2
点 $ O $ 是 $ \triangle ABC $ 三条角平分线的交点,即内心。内心到三角形三边的距离相等,设该距离为 $ r $。
直角三角形的面积可表示为两直角边乘积的一半,即 $ S_{\triangle ABC} = \frac{1}{2} × AC × BC = \frac{1}{2} × 6 × 8 = 24 \, \text{cm}^2 $。
同时,三角形面积也可表示为三个小三角形 $ \triangle AOB $、$ \triangle BOC $、$ \triangle AOC $ 面积之和,即:
$S_{\triangle ABC} = \frac{1}{2} × AB × r + \frac{1}{2} × BC × r + \frac{1}{2} × AC × r = \frac{1}{2} × (AB + BC + AC) × r$
代入已知值:
$24 = \frac{1}{2} × (10 + 8 + 6) × r$
解得:
$24 = \frac{1}{2} × 24 × r \implies 24 = 12r \implies r = 2$
因此,点 $ O $ 到三边 $ AB $、$ AC $、$ BC $ 的距离均为 $ 2 \, \text{cm} $。
【答案】:2,2,2
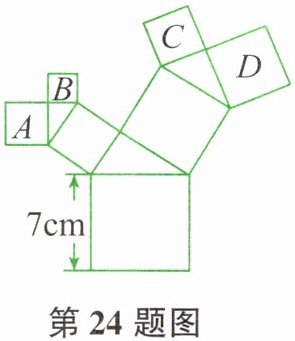
24. 如图所示,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为 7cm,则正方形 A、B、C、D 的面积之和为____$ \mathrm { cm } ^ { 2 } $。

答案:
【解析】:设与正方形A、B相邻的直角三角形的两条直角边分别为$a$、$b$,斜边为$c$;与正方形C、D相邻的直角三角形的两条直角边分别为$d$、$e$,斜边为$f$。
因为所有四边形都是正方形,所以正方形A的面积为$a^2$,正方形B的面积为$b^2$,正方形C的面积为$d^2$,正方形D的面积为$e^2$。
根据勾股定理,对于第一个直角三角形有$a^2 + b^2 = c^2$,即正方形A和B的面积之和为$c^2$;对于第二个直角三角形有$d^2 + e^2 = f^2$,即正方形C和D的面积之和为$f^2$。
观察图形可知,最大的正方形的边长为7cm,其面积为$7^2 = 49$ $cm^2$,且最大正方形的边长对应的斜边是由$c$和$f$为直角边的直角三角形的斜边,所以根据勾股定理可得$c^2 + f^2 = 7^2 = 49$。
因此,正方形A、B、C、D的面积之和为$a^2 + b^2 + d^2 + e^2 = c^2 + f^2 = 49$ $cm^2$。
【答案】:49
因为所有四边形都是正方形,所以正方形A的面积为$a^2$,正方形B的面积为$b^2$,正方形C的面积为$d^2$,正方形D的面积为$e^2$。
根据勾股定理,对于第一个直角三角形有$a^2 + b^2 = c^2$,即正方形A和B的面积之和为$c^2$;对于第二个直角三角形有$d^2 + e^2 = f^2$,即正方形C和D的面积之和为$f^2$。
观察图形可知,最大的正方形的边长为7cm,其面积为$7^2 = 49$ $cm^2$,且最大正方形的边长对应的斜边是由$c$和$f$为直角边的直角三角形的斜边,所以根据勾股定理可得$c^2 + f^2 = 7^2 = 49$。
因此,正方形A、B、C、D的面积之和为$a^2 + b^2 + d^2 + e^2 = c^2 + f^2 = 49$ $cm^2$。
【答案】:49
25. 如图所示,在一棵树的 10m 高 B 处有两只猴子,一只猴子爬下树走到离树 20m 处的池塘 A 处。另一只爬到树顶 D 后直接跃到 A 处,跳跃距离以直线计算。如果两只猴子所经过的距离相等,则这棵树高____m。
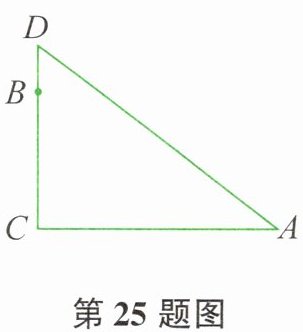

答案:
【解析】:
设树高为$h$米,即$BD = h - 10$米,$CD = h$米。
已知一只猴子从$B$处爬下树走到离树$20$米处的池塘$A$处,所经过的距离为$BC + CA=10 + 20 = 30$米。
另一只猴子从$B$处爬到树顶$D$后直接跃到$A$处,所经过的距离为$BD + DA$,且两只猴子所经过的距离相等,所以$BD + DA = 30$米,即$DA = 30 - BD = 30-(h - 10)=40 - h$米。
在$Rt\triangle ACD$中,$CD = h$米,$CA = 20$米,根据勾股定理$DA^{2}=CD^{2}+CA^{2}$,可得$(40 - h)^{2}=h^{2}+20^{2}$。
展开式子得$1600-80h + h^{2}=h^{2}+400$。
移项化简可得$80h = 1200$,解得$h = 15$米。
【答案】:15
设树高为$h$米,即$BD = h - 10$米,$CD = h$米。
已知一只猴子从$B$处爬下树走到离树$20$米处的池塘$A$处,所经过的距离为$BC + CA=10 + 20 = 30$米。
另一只猴子从$B$处爬到树顶$D$后直接跃到$A$处,所经过的距离为$BD + DA$,且两只猴子所经过的距离相等,所以$BD + DA = 30$米,即$DA = 30 - BD = 30-(h - 10)=40 - h$米。
在$Rt\triangle ACD$中,$CD = h$米,$CA = 20$米,根据勾股定理$DA^{2}=CD^{2}+CA^{2}$,可得$(40 - h)^{2}=h^{2}+20^{2}$。
展开式子得$1600-80h + h^{2}=h^{2}+400$。
移项化简可得$80h = 1200$,解得$h = 15$米。
【答案】:15
查看更多完整答案,请扫码查看


