5. 点 $E$ 是正方形 $ABCD$ 的边 $BC$ 的中点,如果 $DE = 5$,那么正方形 $ABCD$ 的面积是( )。
A.$5$
B.$15$
C.$20$
D.$30$
A.$5$
B.$15$
C.$20$
D.$30$
答案:
【解析】:设正方形 $ABCD$ 的边长为 $a$。因为点 $E$ 是边 $BC$ 的中点,所以 $EC = \frac{a}{2}$。在直角三角形 $DCE$ 中,$DC = a$,$EC = \frac{a}{2}$,$DE = 5$。根据勾股定理可得:$DC^2 + EC^2 = DE^2$,即$a^2 + \left(\frac{a}{2}\right)^2 = 5^2$。化简得:$a^2 + \frac{a^2}{4} = 25$,$\frac{5a^2}{4} = 25$,解得$a^2 = 20$。所以正方形 $ABCD$ 的面积是 $20$。
【答案】:C
【答案】:C
6. 已知菱形的周长为 $24cm$,且有一个内角为 $120^{\circ}$,那么它的一条较长的对角线和面积分别是( )。
A.$6\sqrt{3}cm$,$18\sqrt{3}cm^{2}$
B.$6cm$,$18cm^{2}$
C.$6\sqrt{3}cm$,$36cm^{2}$
D.$6cm$,$18\sqrt{3}cm^{2}$
A.$6\sqrt{3}cm$,$18\sqrt{3}cm^{2}$
B.$6cm$,$18cm^{2}$
C.$6\sqrt{3}cm$,$36cm^{2}$
D.$6cm$,$18\sqrt{3}cm^{2}$
答案:
【解析】:已知菱形的周长为24cm,因为菱形的四条边相等,所以每条边的长度为$24÷4 = 6cm$。
菱形的一个内角为$120^{\circ}$,则与其相邻的内角为$180^{\circ}-120^{\circ}=60^{\circ}$。菱形的对角线互相垂直平分,且每条对角线平分一组对角。设菱形的两条对角线分别为$d_1$(较短对角线)和$d_2$(较长对角线),它们相交于点O,将菱形分成四个直角三角形。
以含$60^{\circ}$角的直角三角形为例,菱形的边长为斜边(6cm),较短对角线的一半为$6×\sin(60^{\circ}÷2)=6×\sin30^{\circ}=6×\frac{1}{2}=3cm$,所以较短对角线$d_1 = 2×3 = 6cm$;较长对角线的一半为$6×\cos(60^{\circ}÷2)=6×\cos30^{\circ}=6×\frac{\sqrt{3}}{2}=3\sqrt{3}cm$,所以较长对角线$d_2 = 2×3\sqrt{3}=6\sqrt{3}cm$。
菱形的面积为两条对角线乘积的一半,即$\frac{1}{2}× d_1× d_2=\frac{1}{2}×6×6\sqrt{3}=18\sqrt{3}cm^{2}$。
综上,较长的对角线为$6\sqrt{3}cm$,面积为$18\sqrt{3}cm^{2}$。
【答案】:A
菱形的一个内角为$120^{\circ}$,则与其相邻的内角为$180^{\circ}-120^{\circ}=60^{\circ}$。菱形的对角线互相垂直平分,且每条对角线平分一组对角。设菱形的两条对角线分别为$d_1$(较短对角线)和$d_2$(较长对角线),它们相交于点O,将菱形分成四个直角三角形。
以含$60^{\circ}$角的直角三角形为例,菱形的边长为斜边(6cm),较短对角线的一半为$6×\sin(60^{\circ}÷2)=6×\sin30^{\circ}=6×\frac{1}{2}=3cm$,所以较短对角线$d_1 = 2×3 = 6cm$;较长对角线的一半为$6×\cos(60^{\circ}÷2)=6×\cos30^{\circ}=6×\frac{\sqrt{3}}{2}=3\sqrt{3}cm$,所以较长对角线$d_2 = 2×3\sqrt{3}=6\sqrt{3}cm$。
菱形的面积为两条对角线乘积的一半,即$\frac{1}{2}× d_1× d_2=\frac{1}{2}×6×6\sqrt{3}=18\sqrt{3}cm^{2}$。
综上,较长的对角线为$6\sqrt{3}cm$,面积为$18\sqrt{3}cm^{2}$。
【答案】:A
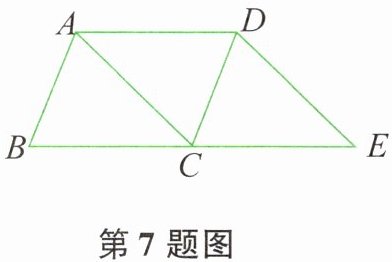
7. 如图所示,将 $\triangle ABC$ 沿 $BC$ 方向平移得到 $\triangle DCE$,连接 $AD$,下列条件中能够判定四边形 $ACED$ 为菱形的是( )。
A.$AB = BC$
B.$AC = BC$
C.$\angle B = 60^{\circ}$
D.$\angle ACB = 60^{\circ}$

A.$AB = BC$
B.$AC = BC$
C.$\angle B = 60^{\circ}$
D.$\angle ACB = 60^{\circ}$
答案:
【解析】:因为△ABC沿BC方向平移得到△DCE,所以AD=BC,AD//BC,AC=DE,AC//DE,因此四边形ACED是平行四边形。要使平行四边形ACED为菱形,需邻边相等,即AC=CE。又因为平移性质可知CE=BC,所以AC=BC时,AC=CE,四边形ACED为菱形。
【答案】:B
【答案】:B
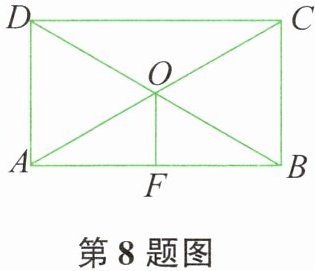
8. 如图所示,在矩形 $ABCD$ 中,$AC$、$BD$ 相交于 $O$,$OF\perp AB$,若 $AC = 2AD$,$OF = 9$,则 $BD$ 的长为( )。
A.$90$
B.$36$
C.$9\sqrt{3}$
D.$18\sqrt{3}$

A.$90$
B.$36$
C.$9\sqrt{3}$
D.$18\sqrt{3}$
答案:
【解析】:在矩形 $ABCD$ 中,对角线 $AC$ 与 $BD$ 相交于点 $O$,根据矩形的性质,对角线相等且互相平分,所以 $AC = BD$,$OA = OC = \frac{1}{2}AC$,$OB = OD = \frac{1}{2}BD$,即 $OA = OB = OC = OD$。
已知 $AC = 2AD$,设 $AD = x$,则 $AC = 2x$。在直角三角形 $ACD$ 中(矩形的四个角为直角),根据勾股定理可得:
$CD^2 + AD^2 = AC^2$,即 $CD^2 + x^2 = (2x)^2$,解得 $CD^2 = 3x^2$,所以 $CD = \sqrt{3}x$。
因为 $AB = CD$(矩形对边相等),所以 $AB = \sqrt{3}x$。
又因为 $OF \perp AB$,且 $O$ 是对角线交点,所以 $OF$ 是 $\triangle ABC$ 的中位线(或由 $OF$ 平行于 $AD$ 且 $O$ 为 $AC$ 中点可得),因此 $OF = \frac{1}{2}AD$。已知 $OF = 9$,则 $\frac{1}{2}AD = 9$,解得 $AD = 18$,即 $x = 18$。
所以 $AC = 2x = 36$,又因为 $AC = BD$,故 $BD = 36$。
【答案】:B
已知 $AC = 2AD$,设 $AD = x$,则 $AC = 2x$。在直角三角形 $ACD$ 中(矩形的四个角为直角),根据勾股定理可得:
$CD^2 + AD^2 = AC^2$,即 $CD^2 + x^2 = (2x)^2$,解得 $CD^2 = 3x^2$,所以 $CD = \sqrt{3}x$。
因为 $AB = CD$(矩形对边相等),所以 $AB = \sqrt{3}x$。
又因为 $OF \perp AB$,且 $O$ 是对角线交点,所以 $OF$ 是 $\triangle ABC$ 的中位线(或由 $OF$ 平行于 $AD$ 且 $O$ 为 $AC$ 中点可得),因此 $OF = \frac{1}{2}AD$。已知 $OF = 9$,则 $\frac{1}{2}AD = 9$,解得 $AD = 18$,即 $x = 18$。
所以 $AC = 2x = 36$,又因为 $AC = BD$,故 $BD = 36$。
【答案】:B
9. 正方形具有而菱形不一定具有的性质是( )。
A.对角线相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.四条边相等
A.对角线相等
B.对角线互相垂直平分
C.对角线平分一组对角
D.四条边相等
答案:
【解析】:
首先,我们分析正方形和菱形的性质:
* 正方形:四条边相等,每个角都是直角,对角线相等且互相垂直平分,对角线平分一组对角。
* 菱形:四条边相等,对角线互相垂直平分,对角线平分一组对角,但不一定每个角都是直角,对角线也不一定相等。
接下来,我们逐一对比选项:
A. 对角线相等:这是正方形具有而菱形不一定具有的性质。
B. 对角线互相垂直平分:这是正方形和菱形都具有的性质。
C. 对角线平分一组对角:这也是正方形和菱形都具有的性质。
D. 四条边相等:这是正方形和菱形都具有的性质。
因此,正方形具有而菱形不一定具有的性质是对角线相等。
【答案】:A
首先,我们分析正方形和菱形的性质:
* 正方形:四条边相等,每个角都是直角,对角线相等且互相垂直平分,对角线平分一组对角。
* 菱形:四条边相等,对角线互相垂直平分,对角线平分一组对角,但不一定每个角都是直角,对角线也不一定相等。
接下来,我们逐一对比选项:
A. 对角线相等:这是正方形具有而菱形不一定具有的性质。
B. 对角线互相垂直平分:这是正方形和菱形都具有的性质。
C. 对角线平分一组对角:这也是正方形和菱形都具有的性质。
D. 四条边相等:这是正方形和菱形都具有的性质。
因此,正方形具有而菱形不一定具有的性质是对角线相等。
【答案】:A
10. 若菱形的一个内角为 $120^{\circ}$,且边长为 $5$,则较长的对角线长为______。
答案:
【解析】:菱形的对角线互相垂直平分,且平分一组对角。已知菱形的一个内角为$120^{\circ}$,则其邻角为$60^{\circ}$。设菱形$ABCD$,$\angle BAD = 120^{\circ}$,边长$AB = 5$,对角线$AC$和$BD$相交于点$O$。则$\angle BAO = 60^{\circ}$(因为对角线平分内角),$\triangle ABO$是直角三角形,其中$\angle AOB = 90^{\circ}$,$AB = 5$,$\angle BAO = 60^{\circ}$。在$Rt\triangle ABO$中,$\sin\angle BAO=\frac{BO}{AB}$,所以$BO = AB\cdot\sin60^{\circ}=5×\frac{\sqrt{3}}{2}=\frac{5\sqrt{3}}{2}$,则较长的对角线$BD = 2BO = 5\sqrt{3}$。
【答案】:$5\sqrt{3}$
【答案】:$5\sqrt{3}$
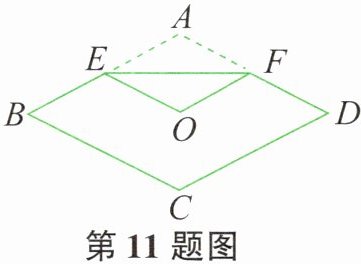
11. 如图所示,将菱形纸片 $ABCD$ 折叠,使点 $A$ 恰好落在菱形的对称中心 $O$ 处,折痕为 $EF$。若菱形 $ABCD$ 的边长为 $2cm$,$\angle A = 120^{\circ}$,则 $EF= $______$cm$。

答案:
【解析】:
连接 $BD$、$AC$,$AC$ 与 $BD$ 相交于点 $O$。
因为四边形 $ABCD$ 是菱形,所以 $AC \perp BD$,且 $AC$ 平分 $\angle BAD$,$BD$ 平分 $\angle ABC$。
已知 $\angle BAD = 120^{\circ}$,所以 $\angle BAC=\frac{1}{2}\angle BAD = 60^{\circ}$,$\angle AOB = 90^{\circ}$。
又因为菱形的边长为 $2cm$,即 $AB = 2cm$,在 $Rt\triangle ABO$ 中,$\angle ABO = 30^{\circ}$,根据 $30^{\circ}$ 所对直角边是斜边的一半,可得 $AO=\frac{1}{2}AB = 1cm$,$BO=\sqrt{AB^{2}-AO^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}cm$。
因为点 $A$ 折叠后落在 $O$ 处,折痕为 $EF$,所以 $EF$ 垂直平分 $AO$,设 $EF$ 与 $AO$ 相交于点 $G$,则 $AG = GO=\frac{1}{2}AO=\frac{1}{2}cm$。
由于 $EF$ 与 $BD$ 平行(菱形对角线互相垂直平分且平分对角,折叠后 $EF$ 与 $BD$ 有平行关系),且 $EF$ 垂直平分 $AO$,$\triangle AEF$ 与 $\triangle ABD$ 相似(因为 $\angle EAG=\angle BAO$,$\angle AGE=\angle AOB = 90^{\circ}$,两角对应相等的两个三角形相似)。
根据相似三角形的性质,$\frac{EF}{BD}=\frac{AG}{AO}$,已知 $BD = 2BO = 2\sqrt{3}cm$,$AG=\frac{1}{2}cm$,$AO = 1cm$,则 $\frac{EF}{2\sqrt{3}}=\frac{\frac{1}{2}}{1}$,解得 $EF=\sqrt{3}cm$。
【答案】:$\sqrt{3}$
连接 $BD$、$AC$,$AC$ 与 $BD$ 相交于点 $O$。
因为四边形 $ABCD$ 是菱形,所以 $AC \perp BD$,且 $AC$ 平分 $\angle BAD$,$BD$ 平分 $\angle ABC$。
已知 $\angle BAD = 120^{\circ}$,所以 $\angle BAC=\frac{1}{2}\angle BAD = 60^{\circ}$,$\angle AOB = 90^{\circ}$。
又因为菱形的边长为 $2cm$,即 $AB = 2cm$,在 $Rt\triangle ABO$ 中,$\angle ABO = 30^{\circ}$,根据 $30^{\circ}$ 所对直角边是斜边的一半,可得 $AO=\frac{1}{2}AB = 1cm$,$BO=\sqrt{AB^{2}-AO^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}cm$。
因为点 $A$ 折叠后落在 $O$ 处,折痕为 $EF$,所以 $EF$ 垂直平分 $AO$,设 $EF$ 与 $AO$ 相交于点 $G$,则 $AG = GO=\frac{1}{2}AO=\frac{1}{2}cm$。
由于 $EF$ 与 $BD$ 平行(菱形对角线互相垂直平分且平分对角,折叠后 $EF$ 与 $BD$ 有平行关系),且 $EF$ 垂直平分 $AO$,$\triangle AEF$ 与 $\triangle ABD$ 相似(因为 $\angle EAG=\angle BAO$,$\angle AGE=\angle AOB = 90^{\circ}$,两角对应相等的两个三角形相似)。
根据相似三角形的性质,$\frac{EF}{BD}=\frac{AG}{AO}$,已知 $BD = 2BO = 2\sqrt{3}cm$,$AG=\frac{1}{2}cm$,$AO = 1cm$,则 $\frac{EF}{2\sqrt{3}}=\frac{\frac{1}{2}}{1}$,解得 $EF=\sqrt{3}cm$。
【答案】:$\sqrt{3}$
查看更多完整答案,请扫码查看


