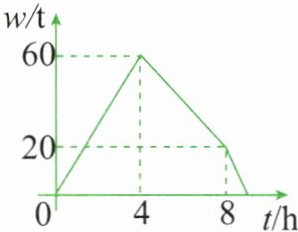
4. 某仓库调拨一批物资,调进物资共用$8h$,调进物资$4h$后同时开始调出物资(调进与调出物资的速度均保持不变)。该仓库库存物资$w(t)与时间t(h)$之间的函数关系如图所示,则这批物资从开始调进到全部调出所需要的时间是( )。
A.$8.4h$
B.$8.6h$
C.$8.8h$
D.$9h$

A.$8.4h$
B.$8.6h$
C.$8.8h$
D.$9h$
答案:
【解析】:
分析图象可知,在0到4小时之间,仓库库存物资从0增加到60吨,
因此调进物资的速度为每小时15吨。
在4到8小时之间,调进物资的同时调出物资,库存从60吨减少到20吨,
即4小时内减少了40吨,
因此在这4小时内,调出比调进多40吨,每小时多10吨。
设调出物资的速度为$v$吨/小时,
那么有:$v-15=10\Rightarrow v=25$,
即调出物资的速度为25吨/小时。
在8小时后,库存物资为20吨,需要全部调出。
由于调进已经停止,
所以所需时间为:$20÷25=0.8$(小时),
从开始到全部调出所需的总时间为:$8+0.8=8.8$(小时)。
【答案】:C
分析图象可知,在0到4小时之间,仓库库存物资从0增加到60吨,
因此调进物资的速度为每小时15吨。
在4到8小时之间,调进物资的同时调出物资,库存从60吨减少到20吨,
即4小时内减少了40吨,
因此在这4小时内,调出比调进多40吨,每小时多10吨。
设调出物资的速度为$v$吨/小时,
那么有:$v-15=10\Rightarrow v=25$,
即调出物资的速度为25吨/小时。
在8小时后,库存物资为20吨,需要全部调出。
由于调进已经停止,
所以所需时间为:$20÷25=0.8$(小时),
从开始到全部调出所需的总时间为:$8+0.8=8.8$(小时)。
【答案】:C
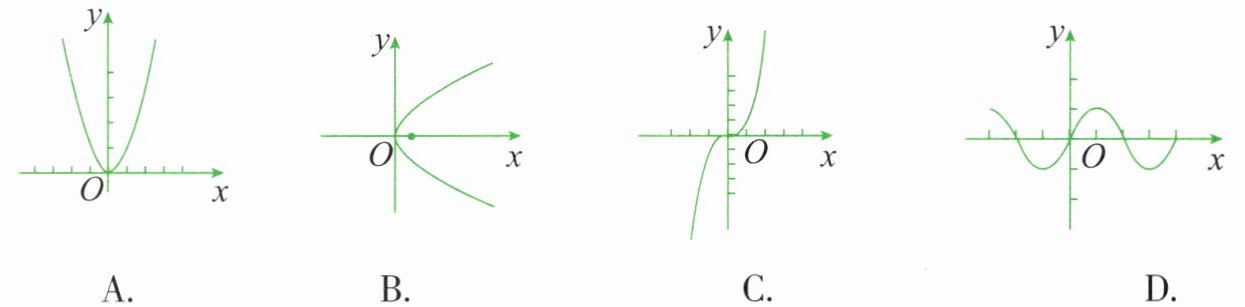
5. 下列各曲线中不能表示$y是x$的函数的是( )。

答案:
【解析】:根据函数的定义,对于每一个确定的$x$值,都有唯一确定的$y$值与之对应。可以通过“垂直于$x$轴的直线与曲线最多有一个交点”来判断。
选项A:是开口向上的抛物线,对于任意$x$,都有唯一$y$值,能表示函数。
选项B:从图像看,当$x>0$时,存在一个$x$值对应两个$y$值(例如第一象限和第四象限各有一个点),不满足函数定义中$y$值的唯一性,不能表示函数。
选项C:图像是一条曲线,对于每个$x$,都有唯一$y$值,能表示函数。
选项D:是波浪线,对于任意$x$,都有唯一$y$值,能表示函数。
【答案】:B
选项A:是开口向上的抛物线,对于任意$x$,都有唯一$y$值,能表示函数。
选项B:从图像看,当$x>0$时,存在一个$x$值对应两个$y$值(例如第一象限和第四象限各有一个点),不满足函数定义中$y$值的唯一性,不能表示函数。
选项C:图像是一条曲线,对于每个$x$,都有唯一$y$值,能表示函数。
选项D:是波浪线,对于任意$x$,都有唯一$y$值,能表示函数。
【答案】:B
6. 已知两个变量$x和y$,它们之间的$3$组对应值如下表所示,则$y与x$之间的函数关系式可能是( )。
| $x$ | $-1$ | $0$ | $1$ |
| $y$ | $-1$ | $1$ | $3$ |
A.$y = x$
B.$y = 2x + 1$
C.$y = x^{2} + x + 1$
D.$y = \frac{3}{x}$
| $x$ | $-1$ | $0$ | $1$ |
| $y$ | $-1$ | $1$ | $3$ |
A.$y = x$
B.$y = 2x + 1$
C.$y = x^{2} + x + 1$
D.$y = \frac{3}{x}$
答案:
【解析】:
对于选项A: $y = x$
当$x = -1$时, $y = -1$,满足;
当$x = 0$时, $y = 0$,与表中的$y = 1$不符;
当$x = 1$时, $y = 1$,与表中的$y = 3$不符;
所以A选项不正确。
对于选项B: $y = 2x + 1$
当$x = -1$时, $y = 2(-1) + 1 = -1$,满足;
当$x = 0$时, $y = 2(0) + 1 = 1$,满足;
当$x = 1$时, $y = 2(1) + 1 = 3$,满足;
所以B选项正确。
对于选项C: $y = x^{2} + x + 1$
当$x = -1$时, $y = (-1)^{2} - 1 + 1 = 1$,与表中的$y = -1$不符;
所以C选项不正确。
对于选项D: $y = \frac{3}{x}$
当$x = 0$时, $y$的值是无定义的,因为分母为0,与表中的$y = 1$不符;
所以D选项不正确。
综上所述,只有B选项满足所有给定的条件。
【答案】:B
对于选项A: $y = x$
当$x = -1$时, $y = -1$,满足;
当$x = 0$时, $y = 0$,与表中的$y = 1$不符;
当$x = 1$时, $y = 1$,与表中的$y = 3$不符;
所以A选项不正确。
对于选项B: $y = 2x + 1$
当$x = -1$时, $y = 2(-1) + 1 = -1$,满足;
当$x = 0$时, $y = 2(0) + 1 = 1$,满足;
当$x = 1$时, $y = 2(1) + 1 = 3$,满足;
所以B选项正确。
对于选项C: $y = x^{2} + x + 1$
当$x = -1$时, $y = (-1)^{2} - 1 + 1 = 1$,与表中的$y = -1$不符;
所以C选项不正确。
对于选项D: $y = \frac{3}{x}$
当$x = 0$时, $y$的值是无定义的,因为分母为0,与表中的$y = 1$不符;
所以D选项不正确。
综上所述,只有B选项满足所有给定的条件。
【答案】:B
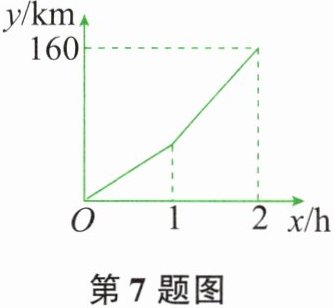
7. 一辆汽车在行驶过程中,路程$y(km)与时间x(h)$之间的函数关系如图所示。当$0\leq x\leq 1$时,$y关于x的函数解析式为y = 60x$;那么当$1\leq x\leq 2$时,$y关于x$的函数解析式为____。

答案:
【解析】:
由图可知,当$1\leq x\leq 2$时,设$y$关于$x$的函数解析式为$y=kx+b$($k\neq0$)。
已知直线$y=kx+b$过点$(1,60)$和$(2,160)$,将这两点代入$y=kx+b$可得方程组:
$\begin{cases}k+b=60,\\2k+b=160.\end{cases}$
用第二个方程$2k+b=160$减去第一个方程$k+b=60$,可得:
$(2k+b)-(k+b)=160-60$,
$2k+b-k-b=100$,
$k=100$。
将$k=100$代入$k+b=60$,可得:
$100+b=60$,
$b=60-100=-40$。
所以,当$1\leq x\leq 2$时,$y$关于$x$的函数解析式为$y=100x-40$。
【答案】:$y=100x-40$
由图可知,当$1\leq x\leq 2$时,设$y$关于$x$的函数解析式为$y=kx+b$($k\neq0$)。
已知直线$y=kx+b$过点$(1,60)$和$(2,160)$,将这两点代入$y=kx+b$可得方程组:
$\begin{cases}k+b=60,\\2k+b=160.\end{cases}$
用第二个方程$2k+b=160$减去第一个方程$k+b=60$,可得:
$(2k+b)-(k+b)=160-60$,
$2k+b-k-b=100$,
$k=100$。
将$k=100$代入$k+b=60$,可得:
$100+b=60$,
$b=60-100=-40$。
所以,当$1\leq x\leq 2$时,$y$关于$x$的函数解析式为$y=100x-40$。
【答案】:$y=100x-40$
8. 市场上一种豆子每千克售$8$元,豆子总的售价$y$(元)与所售豆子的数量$x(kg)$之间的关系为____。当售出$5kg$豆子时,总售价为____元;当售出$10kg$豆子时,总售价为____元。
答案:
【解析】:
根据题目描述,豆子的售价与所售豆子的数量之间的关系是线性的,即总售价$y$与所售豆子的数量$x$之间的关系可以表示为$y=kx$,其中$k$是每千克豆子的售价。
题目中给出每千克豆子售8元,即$k=8$,所以豆子总的售价$y$(元)与所售豆子的数量$x(kg)$之间的关系为$y=8x$。
当售出$5kg$豆子时,将$x=5$代入$y=8x$,得到总售价为$y=8×5=40$元。
当售出$10kg$豆子时,将$x=10$代入$y=8x$,得到总售价为$y=8×10=80$元。
【答案】:
$y=8x$;$40$;$80$。
根据题目描述,豆子的售价与所售豆子的数量之间的关系是线性的,即总售价$y$与所售豆子的数量$x$之间的关系可以表示为$y=kx$,其中$k$是每千克豆子的售价。
题目中给出每千克豆子售8元,即$k=8$,所以豆子总的售价$y$(元)与所售豆子的数量$x(kg)$之间的关系为$y=8x$。
当售出$5kg$豆子时,将$x=5$代入$y=8x$,得到总售价为$y=8×5=40$元。
当售出$10kg$豆子时,将$x=10$代入$y=8x$,得到总售价为$y=8×10=80$元。
【答案】:
$y=8x$;$40$;$80$。
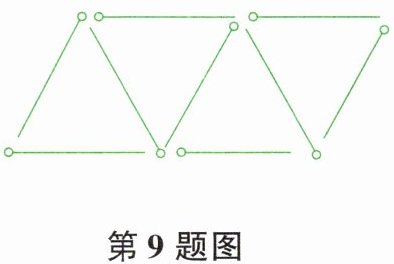
9. 如图所示,用火柴棒搭三角形。搭$1个三角形需3$根火柴棒,搭$2个三角形需5$根火柴棒,搭$3个三角形需7$根火柴棒,照这样的规律搭下去,搭$n个三角形需s$根火柴棒。$s与n$之间的关系可以用式子表示为____。

答案:
【解析】:观察题目可知,搭1个三角形需3根火柴棒,即$s = 3$;搭2个三角形需5根火柴棒,比搭1个三角形多了2根;搭3个三角形需7根火柴棒,比搭2个三角形又多了2根。由此可发现规律,每多搭1个三角形,就需要增加2根火柴棒。
我们可以将搭$n$个三角形所需火柴棒的数量表示为:第一个三角形用3根,后面$(n - 1)$个三角形每个都比前一个多2根,所以总共需要的火柴棒数量$s = 3 + 2(n - 1)$。
对这个式子进行化简:$s = 3 + 2n - 2 = 2n + 1$。
为了验证这个规律,当$n = 1$时,$s = 2×1 + 1 = 3$,符合题意;当$n = 2$时,$s = 2×2 + 1 = 5$,符合题意;当$n = 3$时,$s = 2×3 + 1 = 7$,也符合题意。所以$s$与$n$之间的关系为$s = 2n + 1$。
【答案】:$s = 2n + 1$
我们可以将搭$n$个三角形所需火柴棒的数量表示为:第一个三角形用3根,后面$(n - 1)$个三角形每个都比前一个多2根,所以总共需要的火柴棒数量$s = 3 + 2(n - 1)$。
对这个式子进行化简:$s = 3 + 2n - 2 = 2n + 1$。
为了验证这个规律,当$n = 1$时,$s = 2×1 + 1 = 3$,符合题意;当$n = 2$时,$s = 2×2 + 1 = 5$,符合题意;当$n = 3$时,$s = 2×3 + 1 = 7$,也符合题意。所以$s$与$n$之间的关系为$s = 2n + 1$。
【答案】:$s = 2n + 1$
查看更多完整答案,请扫码查看


