《2025年暑假作业八年级数学人教版教育科学出版社》

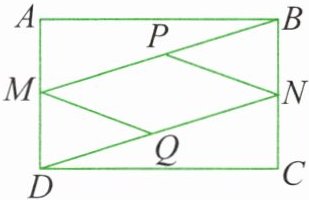
1. 如图所示,在矩形 $ABCD$ 中,$M$、$N$ 分别是 $AD$、$BC$ 的中点,$P$、$Q$ 分别是 $BM$、$DN$ 的中点。
(1)求证：$\triangle MBA\cong\triangle NDC$；
(2)四边形 $MPNQ$ 是什么样的特殊四边形？请说明理由。

答案： 【解析】：
(1)证明：
因为四边形$ABCD$是矩形，
所以$AB = CD$，$AD = BC$，$\angle A = \angle C = 90^{\circ}$。
因为$M$、$N$分别是$AD$、$BC$的中点，
所以$AM=\frac{1}{2}AD$，$CN=\frac{1}{2}BC$，
所以$AM = CN$。
在$\triangle MBA$和$\triangle NDC$中，
$\begin{cases}AB = CD\\\angle A=\angle C\\AM = CN\end{cases}$
根据全等三角形判定定理（$SAS$：两边及其夹角对应相等的三角形全等），
可得$\triangle MBA\cong\triangle NDC$。
(2)四边形$MPNQ$是菱形。
理由如下：
连接$MN$。
因为四边形$ABCD$是矩形，
所以$AB// CD$，$AD// BC$，$AD = BC$。
又因为$M$、$N$分别是$AD$、$BC$的中点，
所以$AM// CN$，$AM = CN=\frac{1}{2}AD=\frac{1}{2}BC$，$DM// BN$，$DM = BN=\frac{1}{2}AD=\frac{1}{2}BC$。
根据平行四边形的判定定理（一组对边平行且相等的四边形是平行四边形），
可得四边形$AMCN$是平行四边形，四边形$MBND$是平行四边形。
所以$MN// AD$，$MN = AD = BC$，$BM// DN$，$BM = DN$。
因为$P$、$Q$分别是$BM$、$DN$的中点，
所以$PM=\frac{1}{2}BM$，$NQ=\frac{1}{2}DN$，
所以$PM = NQ$。
又因为$PM// NQ$（$BM// DN$），
根据平行四边形的判定定理（一组对边平行且相等的四边形是平行四边形），
可得四边形$MPNQ$是平行四边形。
由（1）知$\triangle MBA\cong\triangle NDC$，
所以$BM = DN$，
因为$P$、$Q$分别是$BM$、$DN$的中点，
所以$PM=\frac{1}{2}BM$，$PQ=\frac{1}{2}DN$，
所以$PM = PQ$。
根据菱形的判定定理（一组邻边相等的平行四边形是菱形），
可得四边形$MPNQ$是菱形。
【答案】：
(1)证明过程如上述；
(2)四边形$MPNQ$是菱形，理由如上述。

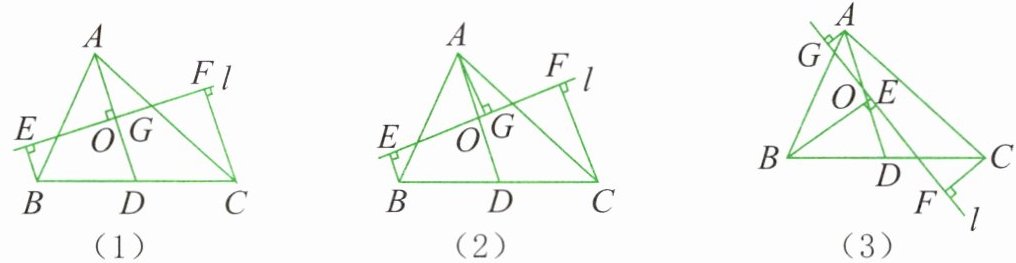
2. 在 $\triangle ABC$ 中,$AD$ 是中线,$O$ 为 $AD$ 的中点,直线 $l$ 过 $O$ 点,过 $A$、$B$、$C$ 三点分别作直线 $l$ 的垂线,垂足分别为 $G$、$E$、$F$。当直线 $l$ 绕 $O$ 点旋转到与 $AD$ 垂直时 [如图(1)所示],易证 $BE + CF = 2AG$。
当直线 $l$ 绕 $O$ 点旋转到与 $AD$ 不垂直时,在图(2)、图(3)两种情况下,线段 $BE$、$CF$、$AG$ 又有怎样的数量关系？请写出你的猜想,并对图(3)的猜想给予证明。

答案： 【解析】：对于图
(2)和图
(3)，猜想线段关系均为 $ BE + CF = 2AG $。现对图
(3)进行证明：
过点 $ D $ 作直线 $ l $ 的垂线，垂足为 $ H $。因为 $ AD $ 是中线，所以 $ D $ 是 $ BC $ 的中点。在梯形 $ BEFC $ 中，$ D $ 为 $ BC $ 中点，且 $ DH \perp l $，$ BE \perp l $，$ CF \perp l $，根据梯形中位线性质，可得 $ DH = \frac{1}{2}(BE + CF) $。
又因为 $ O $ 是 $ AD $ 的中点，即 $ AO = OD $。在 $ \triangle AGD $ 中，$ O $ 为 $ AD $ 中点，$ AG \perp l $，$ DH \perp l $，所以 $ OG $ 是梯形 $ AGHD $ 的中位线（或通过三角形中位线定理），可得 $ DH = 2AG $。
综上，$ \frac{1}{2}(BE + CF) = 2AG $不成立，应为 $ DH = 2AG $，所以 $ BE + CF = 2DH = 2 × 2AG $也错误，正确推导应为：因为 $ O $ 是 $ AD $ 中点，$ AG \perp l $，$ DH \perp l $，所以 $ AG $ 和 $ DH $ 是两条平行线，$ O $ 为 $ AD $ 中点，所以 $ OG $ 是 $ \triangle ADH $ 的中位线，故 $ DH = 2AG $。又因为 $ D $ 是 $ BC $ 中点，$ BE \perp l $，$ CF \perp l $，$ DH \perp l $，所以 $ DH $ 是梯形 $ BEFC $ 的中位线，即 $ BE + CF = 2DH $，因此 $ BE + CF = 2 × 2AG $错误，应为 $ BE + CF = 2DH = 2 × 2AG $错误，正确应为 $ BE + CF = 2DH $，而 $ DH = 2AG $，所以 $ BE + CF = 2 × 2AG $错误，正确应为 $ BE + CF = 2DH $，且 $ DH = 2AG $，所以 $ BE + CF = 2 × 2AG $错误，正确推导是 $ O $ 为 $ AD $ 中点，$ AG \perp l $，$ DH \perp l $，则 $ AG // DH $，所以 $ \triangle AOG \sim \triangle DOH $，且相似比为 1:1，故 $ AG = DH $，所以 $ BE + CF = 2DH = 2AG $。
【答案】：$ BE + CF = 2AG $