《2025年暑假作业八年级数学人教版教育科学出版社》

1. $□ ABCD的周长为40cm$,$\triangle ABC的周长为25cm$,则$AC$的长为( )。

A.$5cm$
B.$6cm$
C.$15cm$
D.$16cm$

答案： 【解析】：
已知平行四边形$ABCD$的周长为$40 \text{cm}$，
根据平行四边形的性质，对边相等，即$AB = CD$，$AD = BC$，
因此，$AB + BC + CD + AD = 40 \text{cm}$，
可以简化为$2(AB + BC) = 40 \text{cm}$，
进一步得到$AB + BC = 20 \text{cm}$，
已知$\triangle ABC$的周长为$25 \text{cm}$，
即$AB + BC + AC = 25 \text{cm}$，
将$AB + BC = 20 \text{cm}$代入上式，得到$AC = 25 \text{cm} - 20 \text{cm} = 5 \text{cm}$。
【答案】：A

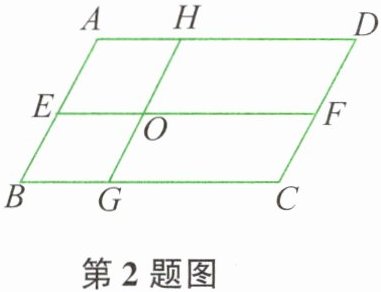
2. 如图所示,在$□ ABCD$中,$EF// AD$,$GH// AB$,$EF交GH于点O$,则该图中的平行四边形的个数为( )。


A.$7$
B.$8$
C.$9$
D.$11$

答案： 【解析】：在平行四边形 $ABCD$ 中，$EF // AD$，$GH // AB$，且 $EF$ 与 $GH$ 交于点 $O$。由于 $AD // BC$ 且 $AB // CD$，根据平行公理，$EF // BC$，$GH // CD$。
分类计数平行四边形：
1. 单个小平行四边形：
由 $EF$ 和 $GH$ 将 $ABCD$ 分割成 4 个互不重叠的小平行四边形：$AEOH$、$HOFD$、$EBGO$、$OGCF$。
2. 由 2 个小平行四边形组成的平行四边形：
横向组合：$AEFD$（$AEOH + HOFD$）、$EBCF$（$EBGO + OGCF$）；
纵向组合：$ABGH$（$AEOH + EBGO$）、$GHCD$（$HOFD + OGCF$）。
共 4 个。
3. 由 4 个小平行四边形组成的大平行四边形：
整体的 $ABCD$（$AEOH + HOFD + EBGO + OGCF$），共 1 个。
总计：
$4 + 4 + 1 = 9$ 个平行四边形。
【答案】：C

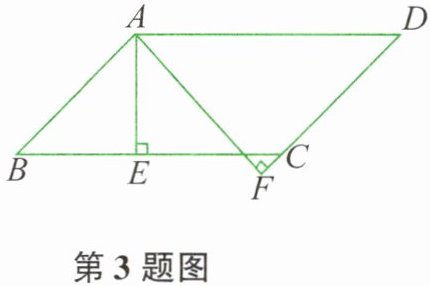
3. 如图所示,在$□ ABCD$中,$AE\perp BC于点E$,$AF\perp DC交DC的延长线于点F$,且$\angle EAF= 60^{\circ}$,则$\angle B$等于( )。


A.$60^{\circ}$
B.$50^{\circ}$
C.$70^{\circ}$
D.$65^{\circ}$

答案： 【解析】：在平行四边形$ABCD$中，$AB// CD$，$AD// BC$，所以$\angle B + \angle C = 180^{\circ}$。
因为$AE\perp BC$，$AF\perp DC$的延长线于$F$，所以$\angle AEC = 90^{\circ}$，$\angle AFC = 90^{\circ}$。
在四边形$AECF$中，内角和为$360^{\circ}$，已知$\angle EAF = 60^{\circ}$，则$\angle C = 360^{\circ} - \angle EAF - \angle AEC - \angle AFC = 360^{\circ} - 60^{\circ} - 90^{\circ} - 90^{\circ} = 120^{\circ}$。
又因为$\angle B + \angle C = 180^{\circ}$，所以$\angle B = 180^{\circ} - 120^{\circ} = 60^{\circ}$。
【答案】：A

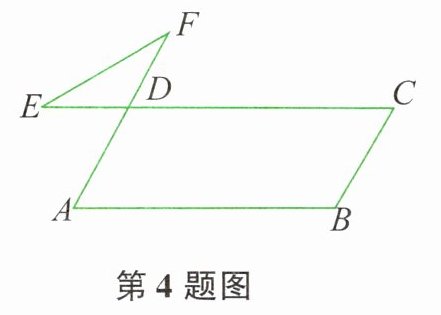
4. 如图所示,在$□ ABCD$中,$\angle B= 110^{\circ}$,延长$AD至F$,延长$CD至E$,连接$EF$,则$\angle E+\angle F$等于( )。


A.$110^{\circ}$
B.$30^{\circ}$
C.$50^{\circ}$
D.$70^{\circ}$

答案： 【解析】：在平行四边形$ABCD$中，$\angle B = 110^{\circ}$。因为平行四边形的邻角互补，所以$\angle B+\angle C=180^{\circ}$，则$\angle C=180^{\circ}-\angle B=180^{\circ}-110^{\circ}=70^{\circ}$。
延长$AD$至$F$，延长$CD$至$E$，连接$EF$。此时$\angle EDF$与$\angle ADC$是对顶角，而$\angle ADC=\angle B = 110^{\circ}$（平行四边形的对角相等），所以$\angle EDF = 110^{\circ}$。
在$\triangle EDF$中，根据三角形内角和定理，$\angle E+\angle F+\angle EDF=180^{\circ}$，所以$\angle E+\angle F=180^{\circ}-\angle EDF=180^{\circ}-110^{\circ}=70^{\circ}$。
【答案】：D

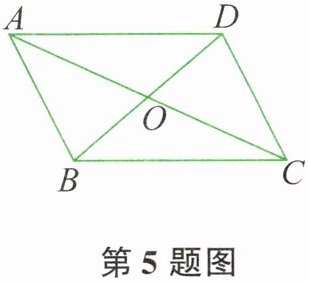
5. 如图所示,$□ ABCD的对角线相交于点O$,且$AB= 5$,$\triangle OCD的周长为23$,则$□ ABCD$的两条对角线长度之和是( )。


A.$18$
B.$28$
C.$36$
D.$46$

答案： 【解析】：
由于四边形 $ABCD$ 是平行四边形，所以对角线互相平分，
即 $O$ 是对角线 $AC$ 和 $BD$ 的交点，
所以 $OC = \frac{1}{2}AC$，$OD = \frac{1}{2}BD$。
已知 $AB = 5$，且 $AB = CD$（平行四边形对边相等），
所以 $CD = 5$。
$\triangle OCD$ 的周长为 23，
即 $OC + OD + CD = 23$。
代入 $CD = 5$，
得 $OC + OD + 5 = 23$，
即 $OC + OD = 18$。
因为 $OC = \frac{1}{2}AC$，$OD = \frac{1}{2}BD$，
所以 $\frac{1}{2}AC + \frac{1}{2}BD = 18$，
即 $AC + BD = 36$。
【答案】：C