《2025年暑假作业八年级数学人教版教育科学出版社》

8. 已知 $ \mathrm { Rt } \triangle A B C $中,$ \angle C = 90 ^ { \circ } $,若 $ a + b = 14 \mathrm { cm } $,$ c = 10 \mathrm { cm } $,则 $ \mathrm { Rt } \triangle A B C $的面积是( )。

A.$ 24 \mathrm { cm } ^ { 2 } $
B.$ 36 \mathrm { cm } ^ { 2 } $
C.$ 48 \mathrm { cm } ^ { 2 } $
D.$ 60 \mathrm { cm } ^ { 2 } $

答案： 【解析】：
已知直角三角形$ \triangle ABC $中，$ \angle C = 90^\circ $，$ a + b = 14 \mathrm{ cm} $，斜边$ c = 10 \mathrm{ cm} $。
根据勾股定理，有$ a^2 + b^2 = c^2 $。
代入已知条件，得$ a^2 + b^2 = 100 $。
又因为$ a + b = 14 $，所以$ (a + b)^2 = 14^2 = 196 $。
展开$ (a + b)^2 $，有$ a^2 + 2ab + b^2 = 196 $。
将$ a^2 + b^2 = 100 $代入上式，得$ 100 + 2ab = 196 $。
解得$ 2ab = 96 $，所以$ ab = 48 $。
直角三角形的面积$ S = \frac{1}{2}ab $，代入$ ab = 48 $，得$ S = \frac{1}{2} × 48 = 24 \mathrm{ cm}^2 $。
【答案】：A.$ 24 \mathrm{ cm}^2 $

9. 等腰三角形底边上的高为 8,周长为 32,则三角形的面积为( )。

A.56
B.48
C.40
D.32

答案： 【解析】：
设等腰三角形的底边为$b$，两腰的长度均为$a$，高为$h$。
根据题意，三角形的周长为32，因此有：
$2a + b = 32 \quad \text{(1)}$
同时，三角形的高$h=8$，根据等腰三角形的性质，底边上的高将底边平分为两段，每段长度为$\frac{b}{2}$。利用勾股定理，可以得到：
$a^2 = \left(\frac{b}{2}\right)^2 + 8^2$
$a^2 = \frac{b^2}{4} + 64 \quad \text{(2)}$
从方程
(1)中解出$b$：
$b = 32 - 2a \quad \text{(3)}$
将方程
(3)代入方程
(2)中，得到：
$a^2 = \frac{(32 - 2a)^2}{4} + 64$
$4a^2 = (32 - 2a)^2 + 256$
$4a^2 = 1024 - 128a + 4a^2 + 256$
$128a = 1280$
$a = 10$
将$a = 10$代入方程
(3)中，得到：
$b = 32 - 2 × 10 = 12$
因此，等腰三角形的底边长度为12，高为8。三角形的面积$S$为：
$S = \frac{1}{2} × b × h = \frac{1}{2} × 12 × 8 = 48$
【答案】：B

10. 三角形的三边长为 $ ( a + b ) ^ { 2 } = c ^ { 2 } + 2 a b $,则这个三角形是( )。

A.等边三角形
B.钝角三角形
C.直角三角形
D.锐角三角形

答案： 【解析】：
首先，我们将给定的等式 $(a + b)^{2} = c^{2} + 2ab$ 进行展开和化简。
$(a + b)^{2} = a^{2} + 2ab + b^{2}$
将这个等式代入原式，得到：
$a^{2} + 2ab + b^{2} = c^{2} + 2ab$
化简后得到：
$a^{2} + b^{2} = c^{2}$
根据勾股定理的逆定理，若在三角形中，三边满足 $a^{2} + b^{2} = c^{2}$，则该三角形是直角三角形。
【答案】：C

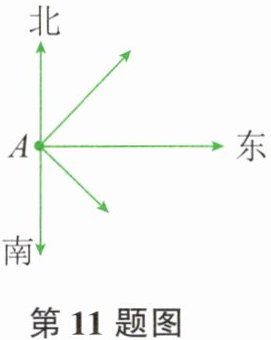
11. 如图所示,已知一轮船以 16 海里/时的速度从港口 A 出发向东北方向航行,另一轮船以 12 海里/时的速度同时从港口 A 出发向东南方向航行。离开港口 2 小时后,两船相距( )。


A.25 海里
B.30 海里
C.35 海里
D.40 海里

答案： 【解析】：由题意可知，两轮船的航行方向分别为东北方向和东南方向，东北方向与东南方向的夹角为90°，即两船的行驶路线构成直角三角形。
轮船1的速度为16海里/时，航行时间为2小时，根据路程=速度×时间，其行驶的路程为：16×2=32海里。
轮船2的速度为12海里/时，航行时间为2小时，其行驶的路程为：12×2=24海里。
此时两船的距离为直角三角形的斜边，根据勾股定理，两船相距：√(32²+24²)=√(1024+576)=√1600=40海里。
【答案】：D

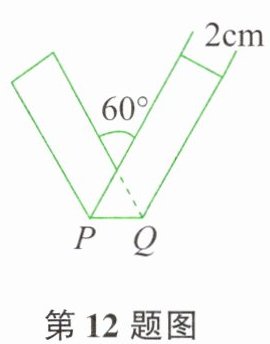
12. 宽为 2cm 的长方形纸条折叠后的形状如图所示,折痕 PQ 的长是( )。


A.$ \frac { 2 } { 3 } \sqrt { 3 } \mathrm { cm } $
B.$ \frac { 4 } { 3 } \sqrt { 3 } \mathrm { cm } $
C.$ \sqrt { 5 } \mathrm { cm } $
D.2cm

答案： 【解析】：
由题意可知，折痕$PQ$是长方形的对称轴。
折叠后，折痕与宽的夹角为$60^\circ$，
所以折痕的一半与宽的一半构成一个直角三角形，
其中宽的一半为1cm，夹角为$60^\circ$。
利用三角函数，设折痕的一半为$x$，
则有：$\tan 60^\circ = \frac{1}{x} \implies x = \frac{1}{\tan 60^\circ} = \frac{1}{\sqrt{3}} = \frac{\sqrt{3}}{3}$。
所以，折痕$PQ$的长度为：$PQ = 2x = 2 × \frac{\sqrt{3}}{3} × 2 = \frac{4\sqrt{3}}{3} \text{ cm}$。
【答案】：B

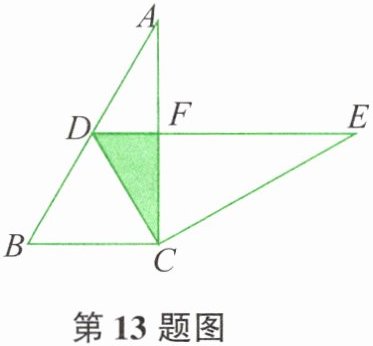
13. 如图所示,在 $ \mathrm { Rt } \triangle A B C $中,$ \angle A C B = 90 ^ { \circ } $,$ \angle A = 30 ^ { \circ } $,$ B C = 2 $。将 $ \triangle A B C $绕点 C 按顺时针方向旋转 n 度后得到 $ \triangle E D C $,此时点 D 在 AB 边上,斜边 DE 交 AC 边于点 F,则 n 的大小和图中阴影部分的面积分别为( )。


A.30,2
B.60,2
C.$ 60, \frac { \sqrt { 3 } } { 2 } $
D.$ 60, \sqrt { 3 } $

答案： 【解析】：在$Rt\triangle ABC$中，$\angle ACB = 90^{\circ}$，$\angle A = 30^{\circ}$，$BC = 2$。根据直角三角形性质，$AB = 2BC = 4$（$30^{\circ}$所对直角边是斜边一半），$AC=\sqrt{AB^{2}-BC^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$，$\angle B=60^{\circ}$。
将$\triangle ABC$绕点$C$顺时针旋转$n$度得到$\triangle EDC$，则$CD = CB = 2$，$CE = CA = 2\sqrt{3}$，$\angle DCE=\angle ACB = 90^{\circ}$，$\angle E=\angle A = 30^{\circ}$。
因为点$D$在$AB$边上，且$CD = CB = 2$，$BC = 2$，所以$\triangle BCD$中，$BC = CD = 2$。又因为$\angle B = 60^{\circ}$，所以$\triangle BCD$是等边三角形（有一个角是$60^{\circ}$的等腰三角形是等边三角形），则$\angle BCD=60^{\circ}$。
旋转角$n=\angle ACD = \angle ACB-\angle BCD=90^{\circ}-60^{\circ}=30^{\circ}$？不对，旋转角是对应边的夹角，$CB$旋转后对应边是$CD$，所以旋转角$n=\angle BCD = 60^{\circ}$（因为$CB$绕$C$顺时针旋转到$CD$，$\angle BCD$就是旋转角）。
此时，$\angle ACD = \angle ACB-\angle BCD=90^{\circ}-60^{\circ}=30^{\circ}$。在$\triangle CDF$中，$\angle DCE = 90^{\circ}$，$\angle ACD = 30^{\circ}$，所以$\angle DCF=\angle ACD = 30^{\circ}$（因为$\angle ACF$就是$\angle ACD$），$\angle DFC = 180^{\circ}-\angle DCF-\angle E$？不对，$\angle E=\angle A = 30^{\circ}$，在$\triangle CFE$中，$\angle E = 30^{\circ}$，$\angle ECF = \angle DCE-\angle DCF=90^{\circ}-30^{\circ}=60^{\circ}$，所以$\angle CFE=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$？或者在$\triangle CDF$中，$\angle CDF$：因为$\triangle BCD$是等边三角形，所以$\angle CDB = 60^{\circ}$，则$\angle CDA = 180^{\circ}-\angle CDB=120^{\circ}$，在$\triangle ADF$中，$\angle A = 30^{\circ}$，$\angle ADF = 120^{\circ}$，所以$\angle AFD=30^{\circ}$，则$\angle DFC = 180^{\circ}-\angle AFD=150^{\circ}$？不，换个思路。
因为$\angle DCF = 30^{\circ}$（$\angle ACD = 30^{\circ}$），$\angle CDF$：在$\triangle ACD$中，$AC = 2\sqrt{3}$，$CD = 2$，$\angle ACD = 30^{\circ}$，由正弦定理$\frac{AD}{\sin\angle ACD}=\frac{CD}{\sin\angle A}$，即$\frac{AD}{\sin30^{\circ}}=\frac{2}{\sin30^{\circ}}$，得$AD = 2$，所以$AD = CD = 2$，则$\triangle ADC$是等腰三角形，$\angle A = \angle ACD = 30^{\circ}$，所以$\angle ADC = 180^{\circ}-30^{\circ}-30^{\circ}=120^{\circ}$。
在$\triangle DFC$中，$\angle DFC = 180^{\circ}-\angle ADC-\angle DCF$？不对，$\angle FDC=\angle ADC = 120^{\circ}$，$\angle DCF = 30^{\circ}$，所以$\angle DFC=180^{\circ}-120^{\circ}-30^{\circ}=30^{\circ}$，则$\triangle DFC$中，$\angle DFC=\angle DCF = 30^{\circ}$，所以$DF = CD = 2$？不对，$\angle DFC = 30^{\circ}$，$\angle DCF = 30^{\circ}$，所以$DF = CD$？$CD = 2$，过$D$作$DG\perp AC$于$G$，在$\triangle CDG$中，$\angle DCG = 30^{\circ}$，$CD = 2$，则$DG=\frac{1}{2}CD = 1$（$30^{\circ}$所对直角边是斜边一半），$CG=\sqrt{CD^{2}-DG^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$。
阴影部分是$\triangle DFC$，其面积为$\frac{1}{2}× CF× DG$。因为$\angle DFC = 30^{\circ}$，在$Rt\triangle DFG$中，$\angle DFG = 30^{\circ}$，$DG = 1$，所以$FG=\frac{DG}{\tan30^{\circ}}=\frac{1}{\frac{\sqrt{3}}{3}}=\sqrt{3}$，则$CF = CG + FG=\sqrt{3}+\sqrt{3}=2\sqrt{3}$？不对，$AC = 2\sqrt{3}$，$CG=\sqrt{3}$，如果$FG=\sqrt{3}$，则$CF = CG + FG = 2\sqrt{3}$，此时$F$与$A$重合，但图中$F$在$AC$上，所以前面有误。
重新分析：$\triangle EDC$中，$\angle E = 30^{\circ}$，$\angle DCE = 90^{\circ}$，所以$\angle CDE = 60^{\circ}$。因为$\triangle BCD$是等边三角形，$\angle CDB = 60^{\circ}$，所以$\angle CDE = \angle CDB = 60^{\circ}$，因此点$F$在$AC$上，$\angle FDC = 60^{\circ}$（因为$\angle CDE = 60^{\circ}$）。
在$\triangle CDF$中，$\angle DCF = \angle ACD = 30^{\circ}$（旋转角$n = 60^{\circ}$，所以$\angle ACD = 90^{\circ}-60^{\circ}=30^{\circ}$），$\angle FDC = 60^{\circ}$，则$\angle DFC=180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$，所以$\triangle CDF$是直角三角形，$\angle DFC = 90^{\circ}$。
在$Rt\triangle CDF$中，$\angle DCF = 30^{\circ}$，$CD = 2$，所以$DF=\frac{1}{2}CD = 1$（$30^{\circ}$所对直角边是斜边一半），$CF=\sqrt{CD^{2}-DF^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$。
阴影部分面积即$\triangle DFC$的面积：$\frac{1}{2}× DF× CF=\frac{1}{2}×1×\sqrt{3}=\frac{\sqrt{3}}{2}$？不对，$\angle DFC = 90^{\circ}$，两直角边是$DF$和$CF$，$DF = 1$，$CF=\sqrt{3}$，面积是$\frac{1}{2}×1×\sqrt{3}=\frac{\sqrt{3}}{2}$。
综上，旋转角$n = 60^{\circ}$，阴影部分面积为$\frac{\sqrt{3}}{2}$。
【答案】：C

14. 在 $ \mathrm { Rt } \triangle A B C $中,$ \angle C = 90 ^ { \circ } $,若 $ a = 5 $,$ b = 12 $,则 $ c = $____。

答案： 【解析】：在直角三角形$ABC$中，由于$\angle C = 90^\circ$，根据勾股定理，有$c^2 = a^2 + b^2$。
题目给出$a = 5$，$b = 12$，代入勾股定理中，得到$c^2 = 5^2 + 12^2 = 25 + 144 = 169$。
由于$c$是斜边，且$c ＞ 0$，所以$c = \sqrt{169} = 13$。
【答案】：13

15. 在 $ \mathrm { Rt } \triangle A B C $中,$ \angle C = 90 ^ { \circ } $,若 $ a = 15 $,$ c = 25 $,则 $ b = $____。

答案： 【解析】：在直角三角形$ABC$中，已知$\angle C = 90^{\circ}$，$a = 15$，$c = 25$。
根据勾股定理，有$a^{2} + b^{2} = c^{2}$。
代入已知值，得到$15^{2} + b^{2} = 25^{2}$。
即$225 + b^{2} = 625$。
解这个方程，得到$b^{2} = 400$。
进一步求解，得到$b = 20$（负值舍去，因为边长不能为负）。
【答案】：20

16. 在 $ \mathrm { Rt } \triangle A B C $中,$ \angle C = 90 ^ { \circ } $,若 $ c = 61 $,$ b = 60 $,则 $ a = $____。

答案： 【解析】：在直角三角形$ABC$中，由于$\angle C = 90^\circ$，根据勾股定理，有$a^2 + b^2 = c^2$。
题目给出$c = 61$，$b = 60$，需要求$a$。
将已知数值代入勾股定理，得到$a^2 + 60^2 = 61^2$，即$a^2 + 3600 = 3721$。
解这个方程，得到$a^2 = 3721 - 3600 = 121$，所以$a = \sqrt{121} = 11$。
【答案】：11