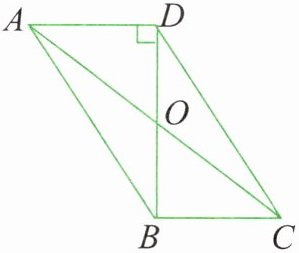
12. 如图所示,四边形$ABCD$是平行四边形,$DB⊥AD$,$AD = 8cm$,$BD = 12cm$,求$BC$、$AC$的长。

答案:
【解析】:因为四边形$ABCD$是平行四边形,根据平行四边形对边相等的性质,所以$BC = AD$。已知$AD = 8cm$,因此$BC = 8cm$。
由于$DB⊥AD$,所以$\triangle ADB$是直角三角形。在$Rt\triangle ADB$中,$AD = 8cm$,$BD = 12cm$,根据勾股定理$AB^2=AD^2 + BD^2$,可得$AB=\sqrt{AD^{2}+BD^{2}}=\sqrt{8^{2}+12^{2}}=\sqrt{64 + 144}=\sqrt{208}=4\sqrt{13}cm$。
在平行四边形$ABCD$中,对角线互相平分,所以$AO = OC$,$BO = OD=\frac{BD}{2}=\frac{12}{2}=6cm$。
在$Rt\triangle AOD$中(因为$DB⊥AD$,所以$\angle ADO = 90^{\circ}$),$AD = 8cm$,$OD = 6cm$,根据勾股定理$AO^2=AD^2 + OD^2$,则$AO=\sqrt{AD^{2}+OD^{2}}=\sqrt{8^{2}+6^{2}}=\sqrt{64 + 36}=\sqrt{100}=10cm$。
因为$AC = 2AO$,所以$AC=2×10 = 20cm$。
【答案】:$BC = 8cm$,$AC = 20cm$
由于$DB⊥AD$,所以$\triangle ADB$是直角三角形。在$Rt\triangle ADB$中,$AD = 8cm$,$BD = 12cm$,根据勾股定理$AB^2=AD^2 + BD^2$,可得$AB=\sqrt{AD^{2}+BD^{2}}=\sqrt{8^{2}+12^{2}}=\sqrt{64 + 144}=\sqrt{208}=4\sqrt{13}cm$。
在平行四边形$ABCD$中,对角线互相平分,所以$AO = OC$,$BO = OD=\frac{BD}{2}=\frac{12}{2}=6cm$。
在$Rt\triangle AOD$中(因为$DB⊥AD$,所以$\angle ADO = 90^{\circ}$),$AD = 8cm$,$OD = 6cm$,根据勾股定理$AO^2=AD^2 + OD^2$,则$AO=\sqrt{AD^{2}+OD^{2}}=\sqrt{8^{2}+6^{2}}=\sqrt{64 + 36}=\sqrt{100}=10cm$。
因为$AC = 2AO$,所以$AC=2×10 = 20cm$。
【答案】:$BC = 8cm$,$AC = 20cm$
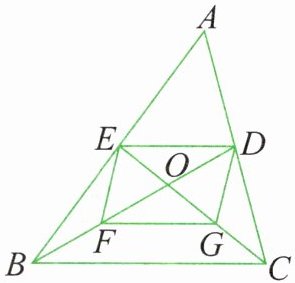
13. 如图所示,$\triangle ABC$中,中线$BD$、$CE交于点O$,$F$、$G分别为OB$、$OC$的中点。求证:四边形$DEFG$为平行四边形。

答案:
【解析】:
1. 由于$BD$和$CE$是$\triangle ABC$的中线,因此$D$和$E$分别是$AC$和$AB$的中点。
2. 根据中点定理,$DE$平行于$BC$且$DE=\frac{1}{2}BC$。
3. 同理,$F$和$G$分别是$OB$和$OC$的中点,因此$FG$平行于$BC$且$FG=\frac{1}{2}BC$。
4. 由于$DE$和$FG$都平行于$BC$且长度相等,因此$DE$平行于$FG$且$DE=FG$。
5. 根据平行四边形的定义,四边形$DEFG$的对边平行且相等,因此四边形$DEFG$是平行四边形。
【答案】:四边形$DEFG$为平行四边形。
1. 由于$BD$和$CE$是$\triangle ABC$的中线,因此$D$和$E$分别是$AC$和$AB$的中点。
2. 根据中点定理,$DE$平行于$BC$且$DE=\frac{1}{2}BC$。
3. 同理,$F$和$G$分别是$OB$和$OC$的中点,因此$FG$平行于$BC$且$FG=\frac{1}{2}BC$。
4. 由于$DE$和$FG$都平行于$BC$且长度相等,因此$DE$平行于$FG$且$DE=FG$。
5. 根据平行四边形的定义,四边形$DEFG$的对边平行且相等,因此四边形$DEFG$是平行四边形。
【答案】:四边形$DEFG$为平行四边形。
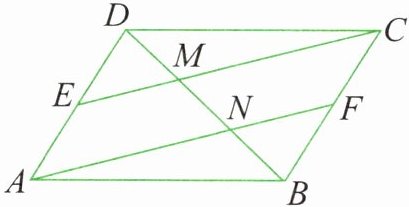
14. 如图所示,$□ ABCD$中,$E$、$F分别为AD$、$BC$的中点,$CE$、$AF分别交BD于M$、$N$。求证:$BN = MN = DM$。

答案:
【解析】:证明:
∵四边形$ABCD$是平行四边形,
∴$AD// BC$,$AD = BC$,$AB// CD$,$AB = CD$。
∵$E$、$F$分别为$AD$、$BC$的中点,
∴$AE=\frac{1}{2}AD$,$CF=\frac{1}{2}BC$,
又
∵$AD = BC$,
∴$AE = CF$。
∵$AD// BC$,即$AE// CF$,
∴四边形$AECF$是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴$AF// CE$(平行四边形的对边平行)。
在$\triangle ADN$中,
∵$AF// CE$(即$EM// AN$),且$E$是$AD$的中点,
∴$M$是$DN$的中点(过三角形一边中点且平行于另一边的直线必平分第三边),
∴$DM = MN$。
在$\triangle BCM$中,
∵$AF// CE$(即$FN// CM$),且$F$是$BC$的中点,
∴$N$是$BM$的中点(过三角形一边中点且平行于另一边的直线必平分第三边),
∴$BN = MN$。
综上,$BN = MN = DM$。
【答案】:$BN = MN = DM$
∵四边形$ABCD$是平行四边形,
∴$AD// BC$,$AD = BC$,$AB// CD$,$AB = CD$。
∵$E$、$F$分别为$AD$、$BC$的中点,
∴$AE=\frac{1}{2}AD$,$CF=\frac{1}{2}BC$,
又
∵$AD = BC$,
∴$AE = CF$。
∵$AD// BC$,即$AE// CF$,
∴四边形$AECF$是平行四边形(一组对边平行且相等的四边形是平行四边形),
∴$AF// CE$(平行四边形的对边平行)。
在$\triangle ADN$中,
∵$AF// CE$(即$EM// AN$),且$E$是$AD$的中点,
∴$M$是$DN$的中点(过三角形一边中点且平行于另一边的直线必平分第三边),
∴$DM = MN$。
在$\triangle BCM$中,
∵$AF// CE$(即$FN// CM$),且$F$是$BC$的中点,
∴$N$是$BM$的中点(过三角形一边中点且平行于另一边的直线必平分第三边),
∴$BN = MN$。
综上,$BN = MN = DM$。
【答案】:$BN = MN = DM$
查看更多完整答案,请扫码查看


