19. 已知$x = 3$,$y = 4$,$z = 5$,那么$\sqrt{yz} ÷ \sqrt{xy}$的最后结果是______。
答案:
【解析】:
首先,根据题目给定的 $x = 3$,$y = 4$,$z = 5$,我们需要求解 $\sqrt{yz} ÷ \sqrt{xy}$。
将 $y$,$z$,$x$ 的值代入表达式,得到:
$\sqrt{4 × 5} ÷ \sqrt{3 × 4}$
根据根号的性质,可以分别计算分子和分母的平方根:
$= \frac{\sqrt{20}}{\sqrt{12}}$
然后,将分子和分母都化简为最简形式:
$= \frac{2\sqrt{5}}{2\sqrt{3}}$
接着,将分子和分母都除以2,得到:
$= \frac{\sqrt{5}}{\sqrt{3}}$
最后,为了得到一个更简洁的表达式,我们可以将分子和分母都乘以 $\sqrt{3}$,得到:
$= \frac{\sqrt{15}}{3}$
【答案】:$\frac{\sqrt{15}}{3}$
首先,根据题目给定的 $x = 3$,$y = 4$,$z = 5$,我们需要求解 $\sqrt{yz} ÷ \sqrt{xy}$。
将 $y$,$z$,$x$ 的值代入表达式,得到:
$\sqrt{4 × 5} ÷ \sqrt{3 × 4}$
根据根号的性质,可以分别计算分子和分母的平方根:
$= \frac{\sqrt{20}}{\sqrt{12}}$
然后,将分子和分母都化简为最简形式:
$= \frac{2\sqrt{5}}{2\sqrt{3}}$
接着,将分子和分母都除以2,得到:
$= \frac{\sqrt{5}}{\sqrt{3}}$
最后,为了得到一个更简洁的表达式,我们可以将分子和分母都乘以 $\sqrt{3}$,得到:
$= \frac{\sqrt{15}}{3}$
【答案】:$\frac{\sqrt{15}}{3}$
20. 若$a$、$b$、$c$均为实数,且$a$、$b$、$c$均不为0,化简$\sqrt{\frac{5a^4c^3}{2b^2}} = $______。
答案:
【解析】:要化简$\sqrt{\frac{5a^4c^3}{2b^2}}$,首先分析根号内各项的符号及化简规则。
因为根号下的表达式必须非负,且$a$、$b$、$c$均不为$0$,分母$2b^2$中$b^2$恒正,所以分子$5a^4c^3$必须非负。$a^4$恒正,$5$为正,因此$c^3\geq0$,即$c\geq0$,又因$c\neq0$,所以$c>0$。
接下来逐步化简:
1. 对于$a^4$,$\sqrt{a^4}=a^2$(因为$a^2$恒非负);
2. 对于$b^2$,$\sqrt{\frac{1}{b^2}}=\frac{1}{|b|}$,由于$b^2$开方后取绝对值,而$b\neq0$,这里默认$b$的符号不影响绝对值结果;
3. 对于$c^3$,$c>0$,所以$\sqrt{c^3}=c\sqrt{c}$;
4. 分母$2$需有理化,分子分母同乘$\sqrt{2}$,得到$\sqrt{\frac{1}{2}}=\frac{\sqrt{2}}{2}$。
综合上述步骤:
$\begin{aligned}\sqrt{\frac{5a^4c^3}{2b^2}}&=\frac{\sqrt{5a^4c^3}}{\sqrt{2b^2}}\\&=\frac{a^2c\sqrt{5c}}{|b|\sqrt{2}}\\&=\frac{a^2c\sqrt{10c}}{2|b|}\end{aligned}$
【答案】:$\frac{a^2c\sqrt{10c}}{2|b|}$
因为根号下的表达式必须非负,且$a$、$b$、$c$均不为$0$,分母$2b^2$中$b^2$恒正,所以分子$5a^4c^3$必须非负。$a^4$恒正,$5$为正,因此$c^3\geq0$,即$c\geq0$,又因$c\neq0$,所以$c>0$。
接下来逐步化简:
1. 对于$a^4$,$\sqrt{a^4}=a^2$(因为$a^2$恒非负);
2. 对于$b^2$,$\sqrt{\frac{1}{b^2}}=\frac{1}{|b|}$,由于$b^2$开方后取绝对值,而$b\neq0$,这里默认$b$的符号不影响绝对值结果;
3. 对于$c^3$,$c>0$,所以$\sqrt{c^3}=c\sqrt{c}$;
4. 分母$2$需有理化,分子分母同乘$\sqrt{2}$,得到$\sqrt{\frac{1}{2}}=\frac{\sqrt{2}}{2}$。
综合上述步骤:
$\begin{aligned}\sqrt{\frac{5a^4c^3}{2b^2}}&=\frac{\sqrt{5a^4c^3}}{\sqrt{2b^2}}\\&=\frac{a^2c\sqrt{5c}}{|b|\sqrt{2}}\\&=\frac{a^2c\sqrt{10c}}{2|b|}\end{aligned}$
【答案】:$\frac{a^2c\sqrt{10c}}{2|b|}$
21. 计算下列各题。
(1) $\sqrt{24} ÷ \sqrt{3}$ (2) $\sqrt{28} × \sqrt{33} ÷ \sqrt{21}$
(3) $\sqrt{16} × \sqrt{\frac{3}{4}} ÷ \sqrt{3}$ (4) $\frac{\sqrt{27} - \sqrt{12}}{\sqrt{3}}$
(5) $\sqrt{3\frac{1}{2}} × (-\frac{1}{6}\sqrt{1\frac{4}{7}}) ÷ \frac{1}{4}\sqrt{5\frac{1}{2}}$ (6) $(\sqrt{2} + \sqrt{3})^2(5 - 2\sqrt{6})$
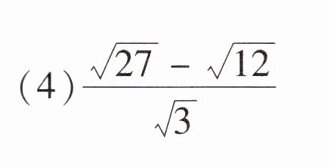
(1) $\sqrt{24} ÷ \sqrt{3}$ (2) $\sqrt{28} × \sqrt{33} ÷ \sqrt{21}$
(3) $\sqrt{16} × \sqrt{\frac{3}{4}} ÷ \sqrt{3}$ (4) $\frac{\sqrt{27} - \sqrt{12}}{\sqrt{3}}$
(5) $\sqrt{3\frac{1}{2}} × (-\frac{1}{6}\sqrt{1\frac{4}{7}}) ÷ \frac{1}{4}\sqrt{5\frac{1}{2}}$ (6) $(\sqrt{2} + \sqrt{3})^2(5 - 2\sqrt{6})$
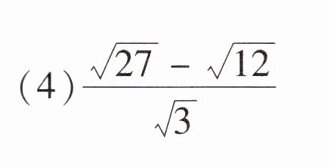
答案:
【解析】:
(1) $\sqrt{24} ÷ \sqrt{3} = \sqrt{24÷3} = \sqrt{8} = 2\sqrt{2}$
(2) $\sqrt{28} × \sqrt{33} ÷ \sqrt{21} = \sqrt{28×33÷21} = \sqrt{44} = 2\sqrt{11}$
(3) $\sqrt{16} × \sqrt{\frac{3}{4}} ÷ \sqrt{3} = 4×\frac{\sqrt{3}}{2}÷\sqrt{3} = 2\sqrt{3}÷\sqrt{3} = 2$
(4) $\frac{\sqrt{27} - \sqrt{12}}{\sqrt{3}} = \frac{3\sqrt{3} - 2\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{\sqrt{3}} = 1$
(5) $\sqrt{3\frac{1}{2}} × (-\frac{1}{6}\sqrt{1\frac{4}{7}}) ÷ \frac{1}{4}\sqrt{5\frac{1}{2}}$
$= \sqrt{\frac{7}{2}} × (-\frac{1}{6}\sqrt{\frac{11}{7}}) × 4\sqrt{\frac{2}{11}}$
$= (-\frac{1}{6}×4) × \sqrt{\frac{7}{2}×\frac{11}{7}×\frac{2}{11}} = -\frac{2}{3}×\sqrt{1} = -\frac{2}{3}$
(6) $(\sqrt{2} + \sqrt{3})^2(5 - 2\sqrt{6}) = (2 + 2\sqrt{6} + 3)(5 - 2\sqrt{6}) = (5 + 2\sqrt{6})(5 - 2\sqrt{6}) = 25 - (2\sqrt{6})^2 = 25 - 24 = 1$
【答案】:
(1)$2\sqrt{2}$;
(2)$2\sqrt{11}$;
(3)2;
(4)1;
(5)$-\frac{2}{3}$;
(6)1
(1) $\sqrt{24} ÷ \sqrt{3} = \sqrt{24÷3} = \sqrt{8} = 2\sqrt{2}$
(2) $\sqrt{28} × \sqrt{33} ÷ \sqrt{21} = \sqrt{28×33÷21} = \sqrt{44} = 2\sqrt{11}$
(3) $\sqrt{16} × \sqrt{\frac{3}{4}} ÷ \sqrt{3} = 4×\frac{\sqrt{3}}{2}÷\sqrt{3} = 2\sqrt{3}÷\sqrt{3} = 2$
(4) $\frac{\sqrt{27} - \sqrt{12}}{\sqrt{3}} = \frac{3\sqrt{3} - 2\sqrt{3}}{\sqrt{3}} = \frac{\sqrt{3}}{\sqrt{3}} = 1$
(5) $\sqrt{3\frac{1}{2}} × (-\frac{1}{6}\sqrt{1\frac{4}{7}}) ÷ \frac{1}{4}\sqrt{5\frac{1}{2}}$
$= \sqrt{\frac{7}{2}} × (-\frac{1}{6}\sqrt{\frac{11}{7}}) × 4\sqrt{\frac{2}{11}}$
$= (-\frac{1}{6}×4) × \sqrt{\frac{7}{2}×\frac{11}{7}×\frac{2}{11}} = -\frac{2}{3}×\sqrt{1} = -\frac{2}{3}$
(6) $(\sqrt{2} + \sqrt{3})^2(5 - 2\sqrt{6}) = (2 + 2\sqrt{6} + 3)(5 - 2\sqrt{6}) = (5 + 2\sqrt{6})(5 - 2\sqrt{6}) = 25 - (2\sqrt{6})^2 = 25 - 24 = 1$
【答案】:
(1)$2\sqrt{2}$;
(2)$2\sqrt{11}$;
(3)2;
(4)1;
(5)$-\frac{2}{3}$;
(6)1
查看更多完整答案,请扫码查看


