《2025年经纶学典学霸题中题八年级物理上册苏科版》

16. 某同学自制了一支温度计,在其测量范围内刻上了$120$格均匀的刻度,他通过实验测定了该温度计各个刻度对应的温度值,并根据实验数据绘制了温度计刻度的格数$(n)与实际准确温度(t)$的关系图像,如图所示.求:

(1)该温度计每$1$格表示的温度是多少?
(2)该温度计的测量范围是多少?
(3)应把$30^{\circ }C$标在此温度计的第几格处?

答案：
(1)1.25℃
(2)-12.5℃~137.5℃
(3)34格
解析:
(1)由图像知,0℃对应的是10格,100℃对应的是90格,则该温度计每1格表示的温度t = $\frac{100}{80}$℃ = 1.25℃.
(2)该温度计在测量范围内有120格,则在0℃以下有10格,最低测量温度$t_0$ = -10×1.25℃ = -12.5℃,100℃以上有30格,最高温度$t_1$ = 100℃ + 30×1.25℃ = 137.5℃,该温度计的测量范围是-12.5℃到137.5℃.
(3)30℃在0℃之上的格数为n = $\frac{30}{1.25}$ = 24,则30℃在此温度计上标的格数$n_1$ = 24格 + 10格 = 34格.

17. 某同学做实验时发现一支温度计不准确,仔细观察发现它的刻度是均匀的.把不准确温度计和标准温度计一同插入水中,发现当实际温度为$0^{\circ }C$时,它的示数为$5^{\circ }C$,当实际温度为$100^{\circ }C$时,它的示数为$95^{\circ }C$.当实际温度为____$^{\circ }C$时,这支温度计的示数等于实际温度值.

答案： 50 解析:这支温度计用95 - 5 = 90格,表示实际的100℃,因此该温度计一格表示的温度值为$\frac{100℃}{90}$ = $\frac{10}{9}$℃.设实际温度为t时,这支温度计显示t,也就是这支温度计用t - 5格,表示实际的t℃,再次表示出该温度计的分度值为$\frac{t}{t - 5}$℃,列等式$\frac{10}{9}$℃ = $\frac{t}{t - 5}$℃,解得t = 50℃.

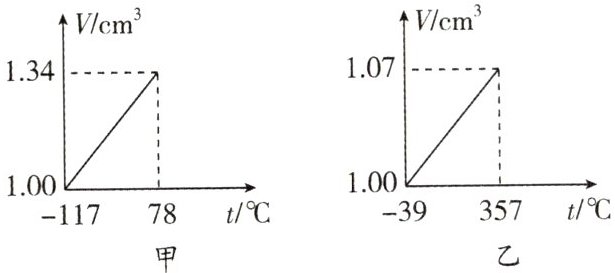
18. (2024·无锡惠山区期中)现有常温下为液态的甲、乙两种物质,如图分别是两种物质的$V-t$图像,若选用相同体积的这两种物质分别制成温度计甲、乙,温度每升高$1^{\circ }C$,感温液体上升相同高度,那么____(填“甲”或“乙”)温度计的玻璃管较细.

答案： 乙 解析:由图像可知,甲物质温度每升高1℃,其体积的增加量为$\Delta V_{甲}$ = $\frac{(1.34 - 1.00)cm^3}{78 - (-117)}$ ≈ 0.0017cm³,乙物质温度每升高1℃,其体积的增加量为$\Delta V_{乙}$ = $\frac{(1.07 - 1.00)cm^3}{357 - (-39)}$ ≈ 0.00018cm³,所以,升高相同温度时甲增大的体积大于乙,即甲比乙的热胀冷缩程度更明显,所以温度每升高1℃,感温液体上升的高度相同时,甲温度计的玻璃管较粗,而乙温度计的玻璃管较细.

19. 某学习小组的同学自制了一个简易温度计,$A$为一塑料瓶,$B$为吸管,通过软木塞与$A$相连,管下端插入水槽中,使管内外水面有一高度差$h$,在不同温度下分别测出对应水柱高度$h$,记录

数据如表:

(1)此温度计的测温原理是____,这个温度计的塑料瓶部分(图中的$A$)相当于常用温度计的____.
(2)若在细管上标记对应温度值,则细管上的温度值从上到下逐渐变____.
(3)用此温度计____(填“能”或“不能”)测$29^{\circ }C$及以上的温度.
(4)当$h= 40.3 cm$时,对应的温度$t= $____$^{\circ }C$.

答案：
(1)气体的热胀冷缩 玻璃泡
(2)大
(3)不能
(4)13
解析:
(1)分析表中的数据,发现随着温度的升高,液柱逐渐变短,仔细观察实验装置图知道,该温度计是利用其上面瓶A中气体热胀冷缩的性质制成的.这个温度计的塑料瓶部分(图中的A)相当于常用温度计的玻璃泡.
(2)由表中的数据知道,当温度为17℃、19℃、21℃、23℃、25℃、27℃时,对应的高度差h分别为:30.0cm、24.9cm、19.7cm、14.6cm、9.4cm、4.3cm.说明水柱高度随着温度的升高而降低,即当水柱越低时,温度越高,所以,从上到下,温度值逐渐增大.
(3)分析表中数据知道,温度每升高2℃,其液柱大约会下降5cm,因为在27℃时的液柱总长只有4.3cm,即小于5cm,故该温度计不能测出29℃及以上的温度.
(4)水柱高为40.3cm与水柱高30.0cm时的高度差为$\Delta h$ = 40.3cm - 30.0cm = 10.3cm.
温度从19℃降低到17℃时的水柱升高的高度差为5.1cm,温度从21℃降低到19℃时的水柱升高的高度差为5.2cm,温度从23℃降低到21℃时水柱升高的高度差为5.1cm,温度从25℃降低到23℃时的水柱升高的高度差为5.2cm,温度从27℃降低到25℃时的水柱升高的高度差为5.1cm,由此可知,温度每变化4℃,高度会变化5.2cm + 5.1cm = 10.3cm.
推算可知,当水柱高为40.3cm与水柱高30.0cm时,温度降低了4℃,故温度为13℃.