第124页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
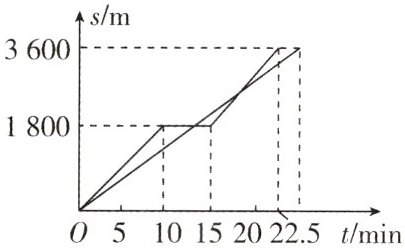
4. 小昭家与图书馆的距离为 3 600 m. 周末, 小昭和爸爸同时从家骑自行车去图书馆. 爸爸先骑行 10 min, 中途休息了 5 min, 再骑行 7.5 min 到达图书馆. 小昭始终以 2.4 m/s 速度骑行, 两人行驶的路程 s 与时间 t 的关系图像如图所示.
(1) 求小昭在途中与爸爸第二次相遇时距图书馆的距离;
(2) 要使小昭在途中能与爸爸恰好相遇两次 (不包括家、图书馆两地), 则他骑车的速度大小应在多大的取值范围内? (除不尽时保留一位小数)
(1) 求小昭在途中与爸爸第二次相遇时距图书馆的距离;
(2) 要使小昭在途中能与爸爸恰好相遇两次 (不包括家、图书馆两地), 则他骑车的速度大小应在多大的取值范围内? (除不尽时保留一位小数)

答案:
(1) $ 900 \, \text{m} $
(2) 大于 $ 2 \, \text{m/s} $ 且小于 $ 2.7 \, \text{m/s} $
解析:
(1) 由图可知, 小昭爸爸在 $ 15 \sim 22.5 \, \text{min} $ 的速度
$ v_1 = \frac{s_1}{t_1} = \frac{1800 \, \text{m}}{7.5 \times 60 \, \text{s}} = 4 \, \text{m/s} $,
由图可知, 小昭在途中与爸爸第二次相遇时, 时间应在 $ 15 \sim 22.5 \, \text{min} $ 范围, 设第二次相遇时小昭所用时间为 $ t $, 小昭运动的距离
$ s = v_2 t = 2.4 \, \text{m/s} \times t \cdots \cdots ① $,
小昭爸爸运动的距离
$ s = 1800 \, \text{m} + 4 \, \text{m/s} \times (t - 15 \times 60 \, \text{s}) \cdots \cdots ② $,
由 ①② 解得 $ t = 1125 \, \text{s}, s = 2700 \, \text{m} $,
第二次相遇时距图书馆的距离
$ s_2 = 3600 \, \text{m} - 2700 \, \text{m} = 900 \, \text{m} $.
(2) 小昭到达图书馆的时间恰好为 $ 22.5 \, \text{min} $ 时, 小昭只能与爸爸相遇一次, 此时小昭的速度
$ v_2 = \frac{s}{t_2} = \frac{3600 \, \text{m}}{22.5 \times 60 \, \text{s}} \approx 2.7 \, \text{m/s} $.
若小昭在 $ 15 \, \text{min} $ 时才追上爸爸, 小昭只能与爸爸相遇一次, 此时小昭的速度 $ v_3 = \frac{s_1}{t_3} = \frac{1800 \, \text{m}}{15 \times 60 \, \text{s}} = 2 \, \text{m/s} $,
要使小昭在途中能与爸爸恰好相遇两次 (不包括家、图书馆两地), 则小昭骑车的速度应大于 $ 2 \, \text{m/s} $ 且小于 $ 2.7 \, \text{m/s} $.
(1) $ 900 \, \text{m} $
(2) 大于 $ 2 \, \text{m/s} $ 且小于 $ 2.7 \, \text{m/s} $
解析:
(1) 由图可知, 小昭爸爸在 $ 15 \sim 22.5 \, \text{min} $ 的速度
$ v_1 = \frac{s_1}{t_1} = \frac{1800 \, \text{m}}{7.5 \times 60 \, \text{s}} = 4 \, \text{m/s} $,
由图可知, 小昭在途中与爸爸第二次相遇时, 时间应在 $ 15 \sim 22.5 \, \text{min} $ 范围, 设第二次相遇时小昭所用时间为 $ t $, 小昭运动的距离
$ s = v_2 t = 2.4 \, \text{m/s} \times t \cdots \cdots ① $,
小昭爸爸运动的距离
$ s = 1800 \, \text{m} + 4 \, \text{m/s} \times (t - 15 \times 60 \, \text{s}) \cdots \cdots ② $,
由 ①② 解得 $ t = 1125 \, \text{s}, s = 2700 \, \text{m} $,
第二次相遇时距图书馆的距离
$ s_2 = 3600 \, \text{m} - 2700 \, \text{m} = 900 \, \text{m} $.
(2) 小昭到达图书馆的时间恰好为 $ 22.5 \, \text{min} $ 时, 小昭只能与爸爸相遇一次, 此时小昭的速度
$ v_2 = \frac{s}{t_2} = \frac{3600 \, \text{m}}{22.5 \times 60 \, \text{s}} \approx 2.7 \, \text{m/s} $.
若小昭在 $ 15 \, \text{min} $ 时才追上爸爸, 小昭只能与爸爸相遇一次, 此时小昭的速度 $ v_3 = \frac{s_1}{t_3} = \frac{1800 \, \text{m}}{15 \times 60 \, \text{s}} = 2 \, \text{m/s} $,
要使小昭在途中能与爸爸恰好相遇两次 (不包括家、图书馆两地), 则小昭骑车的速度应大于 $ 2 \, \text{m/s} $ 且小于 $ 2.7 \, \text{m/s} $.
5. 司机驾车遇到紧急情况时从发现险情到作出反应需要 0.8 s 的时间, 某司机驾车以 20 m/s 的速度匀速前行, 突然发现前方有障碍物, 立即采取紧急刹车措施, 汽车制动后继续向前滑行 2.2 s, 地上刹车痕迹长 20 m. 求:
(1) 司机从发现险情到汽车完全停下来整个过程的平均速度;
(2) 研究表明汽车刹车距离与车速有关, 近似成正比关系, 若汽车以 108 km/h 的速度行驶时, 为了避免追尾事故, 两辆汽车至少保持的距离;
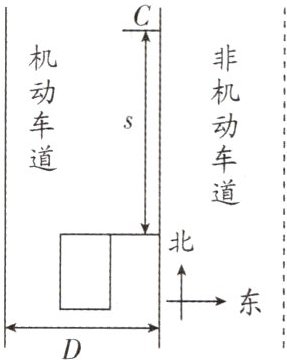
(3) 若司机驾驶车辆正在机动车道上由南向北匀速行驶, 已知机动车道的宽度 D 为 3 m, 轿车长度为 3 m、宽度为 1.8 m, 行驶速度为 36 km/h, 车辆行驶中始终位于机动车道的正中间. 如图, 某一时刻, 小蜀骑自行车在距离轿车正前方 s = 8 m 的 C 处横穿机动车道, 已知自行车长 1.6 m. 若司机没有采取任何措施, 则小蜀要先过公路, 骑车的速度至少是多大, 才能避免与车辆相撞?

(1) 司机从发现险情到汽车完全停下来整个过程的平均速度;
(2) 研究表明汽车刹车距离与车速有关, 近似成正比关系, 若汽车以 108 km/h 的速度行驶时, 为了避免追尾事故, 两辆汽车至少保持的距离;
(3) 若司机驾驶车辆正在机动车道上由南向北匀速行驶, 已知机动车道的宽度 D 为 3 m, 轿车长度为 3 m、宽度为 1.8 m, 行驶速度为 36 km/h, 车辆行驶中始终位于机动车道的正中间. 如图, 某一时刻, 小蜀骑自行车在距离轿车正前方 s = 8 m 的 C 处横穿机动车道, 已知自行车长 1.6 m. 若司机没有采取任何措施, 则小蜀要先过公路, 骑车的速度至少是多大, 才能避免与车辆相撞?
答案:
(1) $ 12 \, \text{m/s} $
(2) $ 54 \, \text{m} $
(3) $ 5 \, \text{m/s} $
解析:
(1) 司机反应时间内汽车通过的路程为 $ s_1 = v_1 t_1 = 20 \, \text{m/s} \times 0.8 \, \text{s} = 16 \, \text{m} $,
司机从发现险情到汽车完全停下来整个过程的平均速度为
$ v = \frac{s_{\text{总}}}{t} = \frac{16 \, \text{m} + 20 \, \text{m}}{0.8 \, \text{s} + 2.2 \, \text{s}} = 12 \, \text{m/s} $.
(2) 若汽车以 $ 108 \, \text{km/h} = 30 \, \text{m/s} $ 的速度行驶时, 制动距离为 $ s_2 = \frac{30 \, \text{m/s}}{20 \, \text{m/s}} \times 20 \, \text{m} = 30 \, \text{m} $,
汽车反应时间内通过的路程为 $ s_3 = v_2 t_2 = 30 \, \text{m/s} \times 0.8 \, \text{s} = 24 \, \text{m} $,
为了避免追尾事故, 两辆汽车至少保持的距离为 $ s_{\text{总}}' = s_2 + s_3 = 30 \, \text{m} + 24 \, \text{m} = 54 \, \text{m} $.
(3) 此时汽车行驶速度 $ 36 \, \text{km/h} = 10 \, \text{m/s} $, 汽车到 $ C $ 处的时间为 $ t_3 = \frac{s}{v_3} = \frac{8 \, \text{m}}{10 \, \text{m/s}} = 0.8 \, \text{s} $,
为了避免与车辆相撞, 此段时间内自行车速度为 $ v_{\text{自行车}} = \frac{s_{\text{自行车}}}{t_3} = \frac{\frac{1}{2} \times (3 \, \text{m} - 1.8 \, \text{m}) + 1.8 \, \text{m} + 1.6 \, \text{m}}{0.8 \, \text{s}} = 5 \, \text{m/s} $.
(1) $ 12 \, \text{m/s} $
(2) $ 54 \, \text{m} $
(3) $ 5 \, \text{m/s} $
解析:
(1) 司机反应时间内汽车通过的路程为 $ s_1 = v_1 t_1 = 20 \, \text{m/s} \times 0.8 \, \text{s} = 16 \, \text{m} $,
司机从发现险情到汽车完全停下来整个过程的平均速度为
$ v = \frac{s_{\text{总}}}{t} = \frac{16 \, \text{m} + 20 \, \text{m}}{0.8 \, \text{s} + 2.2 \, \text{s}} = 12 \, \text{m/s} $.
(2) 若汽车以 $ 108 \, \text{km/h} = 30 \, \text{m/s} $ 的速度行驶时, 制动距离为 $ s_2 = \frac{30 \, \text{m/s}}{20 \, \text{m/s}} \times 20 \, \text{m} = 30 \, \text{m} $,
汽车反应时间内通过的路程为 $ s_3 = v_2 t_2 = 30 \, \text{m/s} \times 0.8 \, \text{s} = 24 \, \text{m} $,
为了避免追尾事故, 两辆汽车至少保持的距离为 $ s_{\text{总}}' = s_2 + s_3 = 30 \, \text{m} + 24 \, \text{m} = 54 \, \text{m} $.
(3) 此时汽车行驶速度 $ 36 \, \text{km/h} = 10 \, \text{m/s} $, 汽车到 $ C $ 处的时间为 $ t_3 = \frac{s}{v_3} = \frac{8 \, \text{m}}{10 \, \text{m/s}} = 0.8 \, \text{s} $,
为了避免与车辆相撞, 此段时间内自行车速度为 $ v_{\text{自行车}} = \frac{s_{\text{自行车}}}{t_3} = \frac{\frac{1}{2} \times (3 \, \text{m} - 1.8 \, \text{m}) + 1.8 \, \text{m} + 1.6 \, \text{m}}{0.8 \, \text{s}} = 5 \, \text{m/s} $.
查看更多完整答案,请扫码查看


