《2025年经纶学典学霸题中题八年级物理上册苏科版》

7. 小红参加了学校组织的远足活动,全程6km.她行走前一半路程的平均速度是6km/h,行走后一半路程的平均速度是4km/h,则她通过全程的平均速度是 ()
A. 4km/h
B. 4.8km/h
C. 5km/h
D. 6km/h

答案： B 解析:她行走前一半路程的时间 $ t_1 = \frac{s_1}{v_1} = \frac{\frac{1}{2} \times 6 \, \text{km}}{6 \, \text{km/h}} = 0.5 \, \text{h} $，行走后一半路程的时间 $ t_2 = \frac{s_2}{v_2} = \frac{\frac{1}{2} \times 6 \, \text{km}}{4 \, \text{km/h}} = 0.75 \, \text{h} $，她通过全程的平均速度是 $ v = \frac{s}{t_1 + t_2} = \frac{6 \, \text{km}}{0.5 \, \text{h} + 0.75 \, \text{h}} = 4.8 \, \text{km/h} $，故B符合题意.

8. 甲、乙两车沿同一条平直马路同向前行,甲速度恒为4m/s,乙车从零开始加速,3t₀后做匀速直线运动,两车运动的s-t图像如图所示.在5t₀时,两车之间的距离刚好为16m.下列说法正确的是 (

)
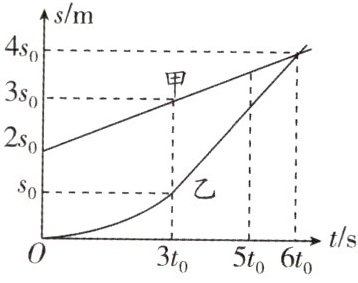
A. 乙车匀速运动时的速度为8m/s
B. t₀= 1s
C. 出发时甲距离乙48m
D. 甲、乙两车相遇时,距离乙车的出发地36m

答案： C 解析:A. 由图像可知，甲的速度 $ v_{\text{甲}} = \frac{3s_0 - 2s_0}{3t_0} = \frac{s_0}{3t_0} = 4 \, \text{m/s} $，则 $ \frac{s_0}{t_0} = 12 \, \text{m/s} $，乙车匀速运动时的速度 $ v_{\text{乙}} = \frac{4s_0 - s_0}{6t_0 - 3t_0} = \frac{s_0}{t_0} = 12 \, \text{m/s} $，故A错误；B. 由题意知，在 $ 5t_0 $ 时两车之间的距离刚好为 $ 16 \, \text{m} $，由图像知， $ 6t_0 $ 时两车相遇，即 $ t_0 $ 时间内 $ s_{\text{甲}} + 16 \, \text{m} = s_{\text{乙}} $，即 $ 4 \, \text{m/s} \cdot t_0 + 16 \, \text{m} = 12 \, \text{m/s} \cdot t_0 $，解得 $ t_0 = 2 \, \text{s} $，故B错误；C. 由 $ \frac{s_0}{t_0} = 12 \, \text{m/s} $ 可得 $ s_0 = 12 \, \text{m/s} \cdot t_0 = 12 \, \text{m/s} \times 2 \, \text{s} = 24 \, \text{m} $，则出发时甲与乙的距离 $ s = 2s_0 = 2 \times 24 \, \text{m} = 48 \, \text{m} $，故C正确；D. 甲、乙两车相遇时，距离乙车的出发地 $ s' = 4s_0 = 4 \times 24 \, \text{m} = 96 \, \text{m} $，故D错误.故选C.

9. “蜻蜓点水”是常见的自然现象,某同学在研究蜻蜓运动的过程中,获得一张如图所示的蜻蜓点水的俯视图片.该图片记录了连续三次点水过程中激起的波纹,已知水波的传播速度和蜻蜓的飞行速度不变,根据图中圆的形状和分布可知 (

)
A. 蜻蜓当时向左飞行,飞行速度比水波传播的速度大
B. 蜻蜓当时向左飞行,飞行速度比水波传播的速度小
C. 蜻蜓当时向右飞行,飞行速度比水波传播的速度大
D. 蜻蜓当时向右飞行,飞行速度比水波传播的速度小

答案： A 解析:蜻蜓连续三次点水过程中激起的波纹，越向左圆圈越小，则水波的传播时间越短，即左侧波纹是后面点水后形成的，所以蜻蜓的飞行方向是从大圆到小圆，即向左飞行；图中中间圆心在右侧圆的外侧，说明蜻蜓点水时，水波还没有到达，即说明蜻蜓飞行的速度比水波的速度大，故A符合题意.

10. 2024年金凤隧道通车,该隧道起于璧山区,穿越缙云山,止于高新区,有效推动了成渝地区双城经济圈建设.小王驾驶汽车驶入隧道,速度与时间的关系如图所示.则小王在0~0.05h做的是____(填“匀速”或“变速”)直线运动;若小王在前0.05h行驶了4.5km,则汽车在0.20h内的平均速度为____km/h.

答案： 变速 $ 82.5 $ 解析:由图可知，小王在 $ 0 \sim 0.05 \, \text{h} $ 内，速度在不断地发生变化，因此做的是变速直线运动.由图可知，小王在 $ 0.05 \sim 0.20 \, \text{h} $ 行驶速度为 $ 80 \, \text{km/h} $，行驶的路程为 $ s_2 = v_2 t_2 = 80 \, \text{km/h} \times (0.20 \, \text{h} - 0.05 \, \text{h}) = 12 \, \text{km} $，
则汽车在 $ 0.20 \, \text{h} $ 内的通过的路程 $ s = s_1 + s_2 = 4.5 \, \text{km} + 12 \, \text{km} = 16.5 \, \text{km} $，
则汽车在 $ 0.20 \, \text{h} $ 内的平均速度 $ v = \frac{s}{t} = \frac{16.5 \, \text{km}}{0.20 \, \text{h}} = 82.5 \, \text{km/h} $.

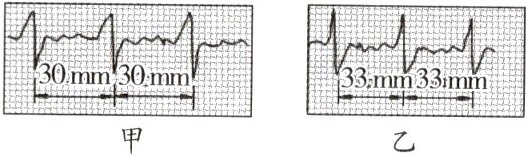
11. 心电图仪可将与人心跳对应的生物电流情况记录在匀速运动的坐标纸上.如图中的每个凸起(波峰)代表一次心跳,若医生测量时记下被检者甲的心跳为60次/分钟.则甲每秒钟心脏跳动的次数为____次;这台心电图仪输出坐标纸的走纸速度大小为____mm/s;乙两次心跳之间的时间间隔为____s.(注:心电图仪走纸速度相同)

答案： $ 1 $ $ 30 $ $ 1.1 $ 解析:由题意知，甲的心跳次数为 $ \frac{60 \, \text{次}}{60 \, \text{s}} = 1 \, \text{次/s} $，即每秒的心跳次数为 $ 1 $ 次.由图甲知，甲两次心跳之间坐标纸移动的距离 $ s = 30 \, \text{mm} $，坐标纸走纸速度 $ v = \frac{s}{t} = \frac{30 \, \text{mm}}{1 \, \text{s}} = 30 \, \text{mm/s} $.由图乙知，乙两次心跳之间坐标纸移动的距离为 $ 33 \, \text{mm} $，则其两次心跳之间的时间 $ t_1 = \frac{s_1}{v} = \frac{33 \, \text{mm}}{30 \, \text{mm/s}} = 1.1 \, \text{s} $.

12. 核心素养 科学思维 某天早晨小边匀速去上学,离开家一段时间后,小边妈妈发现他的作业忘带了,等妈妈出门5min后,小边也想起来作业忘带,于是立刻以相同的速度原路回家,又过了5min他们相遇了.小边和妈妈两人相距的距离s和小边的出发时间t如图所示,则小边的速度为____m/min;妈妈把书拿给小边后,以原路原速回家,则妈妈回到家时,小边离家的距离为____m.

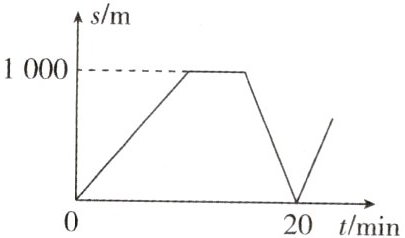
答案： $ 100 $ $ 2000 $ 解析:小边匀速去上学，由图可知妈妈出门追赶他时，两人之间的距离不变，说明两人的速度相同.由图可知，小边和妈妈两人相距的距离 $ s $ 最大为 $ 1000 \, \text{m} $，两人相向而行到相遇共用 $ 5 \, \text{min} $，则小边的速度 $ v = \frac{\frac{1}{2}s}{t} = \frac{\frac{1}{2} \times 1000 \, \text{m}}{5 \, \text{min}} = 100 \, \text{m/min} $.由图可知，妈妈刚出门时，小边与妈妈相距 $ 1000 \, \text{m} $，即此刻小边离家 $ 1000 \, \text{m} $.妈妈出门 $ 5 \, \text{min} $ 时，小边继续向前走 $ 5 \, \text{min} $，向前运动 $ 500 \, \text{m} $，此时小边离家 $ 1500 \, \text{m} $.当小边也立刻以相同的速度原路回家，又过了 $ 5 \, \text{min} $ 他们相遇，小边向回家的方向运动 $ 500 \, \text{m} $，此时小边离家 $ 1000 \, \text{m} $.妈妈从相遇点回到家需要 $ 10 \, \text{min} $，小边在这 $ 10 \, \text{min} $ 向前运动的距离为 $ 1000 \, \text{m} $，则妈妈回到家时小边离家的距离为 $ 1000 \, \text{m} + 1000 \, \text{m} = 2000 \, \text{m} $.