《2025年经纶学典学霸题中题八年级物理上册苏科版》

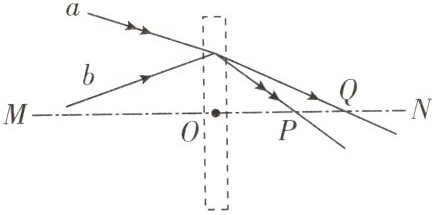
10. 如图所示,虚线框内为一透镜,MN为透镜的主光轴,O是透镜光心,a(双箭头)和b(单箭头)是射向透镜的两条光线.已知光线a通过透镜之后与MN交于P点,光线b通过透镜之后与MN交于Q点.该透镜是____透镜,焦距____(填“大于”“小于”或“等于”)OQ.

答案： 凸 小于 解析:由图中可知,a(双箭头)和b(单箭头)是射向透镜的两条光线,经透镜的作用后光线会聚,由此可判定此透镜为凸透镜;因为平行于主光轴的光线经凸透镜后会聚于焦点,故平行于主光轴的光线经凸透镜后的折射光线与主光轴的交点在P、Q之间,故焦距小于OQ.

11. 小明想知道某块透镜的焦距,进行了如图甲所示的操作(镜面正对着太阳光,在透镜下面放上白纸,且透镜与白纸保持平行),测出透镜与白纸间距s与对应的白纸被烤焦的时间t,绘出图像乙,可判断该透镜的焦距为____cm;若某时刻白纸上所成圆形光斑的直径为透镜直径的一半,且使凸透镜稍远离白纸光斑变大,则此时透镜到白纸的距离

为____cm.

答案：
12 18 解析:当太阳光平行于凸透镜的主光轴入射时,太阳光经过凸透镜会聚于焦点,纸面上成最小最亮的光斑,此时白纸被烤焦的时间最短,由图乙可知,当s=12 cm时对应的白纸被烤焦的时间最短为4 min,所以凸透镜焦距为12 cm.若某时刻白纸上所成圆形光斑的直径为透镜直径的一半,作出凸透镜的光路图如图所示,由图可知圆形光斑可能在1或2的位置.若使凸透镜稍远离白纸光斑变大,则圆形光斑只能在2位置,由几何关系可知:$\frac{OF}{CF}=\frac{AO}{BC}=\frac{2}{1}$,所以$CF=\frac{1}{2}OF=\frac{1}{2}\times12 cm=6 cm$,所以此时透镜到白纸的距离为OC=OF+FC=12 cm+6 cm=18 cm.
　　　　　　

12. (2024·枣庄中考)如图所示,一束光射向凹透镜,请画出该光经过凹透镜、凸透镜的折射光路.

答案：
如图所示
　　　　　　
解析:根据凹透镜的三条特殊光线:延长线过另一侧焦点的光线经凹透镜折射后将平行于主光轴;根据凸透镜的三条特殊光线可知,平行于主光轴的光线经凸透镜折射后将过焦点.

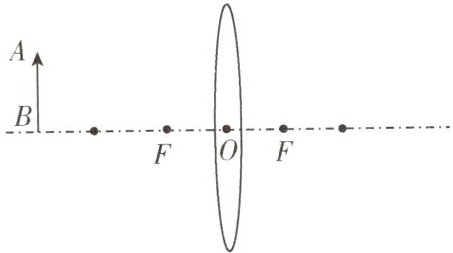
13. 图中物体AB在凸透镜两倍焦距以外,请画出AB经凸透镜所成像A'B'的大致位置.

答案：
如图所示
　　　　　
解析:从A点发出的平行于主光轴的光线经凸透镜折射后过焦点,通过光心的光线传播方向不变,折射光线的交点为A点的像,垂直于主光轴画出像A'B'.

14. (1)小明测焦距时先将凸透镜和光屏的位置固定,将光源从紧贴凸透镜的位置缓慢向外移动到某一位置,光屏上出现一个与透镜直径相近的光斑,此时固定光源、凸透镜,再将光屏远离透镜,移动的过程中,若光屏上光斑的大小____(填“逐渐变大”“几乎不变”或“先变小后变大”),则说明光源到凸透镜的距离即为凸透镜的焦距.
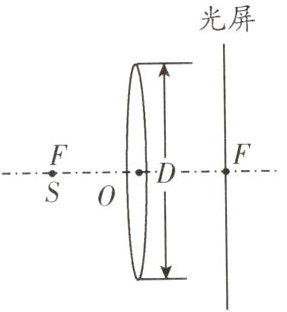
(2)在准确测量焦距时,小明发现在光屏上光斑外侧还有一个暗环,他猜想可能是凸透镜的边框造成的,于是他拆除边框直接将凸透镜固定在原位置,进行实验验证,发现暗环仍然存在.你认为暗环形成的原因是光的直线传播和光的____;若光源在左焦点处,光屏在右焦点处,如图所示,则暗环的面积是____.

答案：

(1)几乎不变
(2)折射 $\frac{3}{4}\pi D^{2}$
解析:
(1)先将凸透镜和光屏的位置固定,将光源从紧贴凸透镜的位置缓慢向外移动到某一位置,光屏上出现一个与透镜直径相近的光斑,说明此时光源正好在透镜的焦点上,从光源发出的光经透镜折射后平行于主光轴,在光屏上形成与透镜直径相近的光斑;再将光屏远离透镜,移动的过程中,光屏上光斑的大小几乎不变,因此光源到凸透镜的距离即为凸透镜的焦距.
(2)透镜边缘以外的光线沿直线传播,边缘以内的光线会发生偏转,二者之间会形成一个没有光线的黑色区域,这就是暗环,因此暗环形成的原因是:透镜外侧沿直线传播的光与经透镜折射的光在屏上形成无光区.
若光源在左焦点处,光屏在右焦点处,如图所示:
　　　　
图中凸透镜正好相当于大三角形的中位线,那么圆环大圆的直径就是2D,半径是D,小圆的直径就是D,半径就是$\frac{D}{2}$,那么暗环的面积为$\Delta S=\pi D^{2}-\pi (\frac{D}{2})^{2}=\frac{3}{4}\pi D^{2}$.