《2025年经纶学典学霸题中题八年级物理上册苏科版》

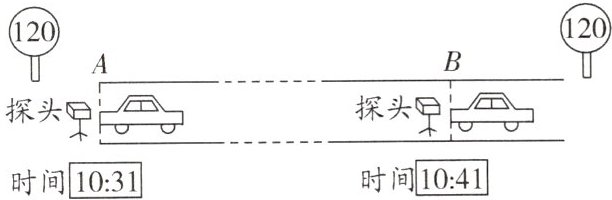
15. 据统计,全国发生的车祸中有超过四分之一是超速引起的。为此,江苏省近年来加大了道路限速监控管理,一种是“定点测速”,即监测汽车在某点的车速；另一种是“区间测速”,就是测算出汽车在某一区间行驶的平均速度。如果超过了该路段的最高限速,即被判为超速。如图,若监测点A、B相距25 km,全程限速120 km/h,一辆轿车通过监测点A、B的速度分别为100 km/h和110 km/h,通过两个监测点的时间如图所示。
(1)采用“定点测速”,该轿车通过监测点A、B时会不会被判超速？
(2)采用“区间测速”,这辆轿车在该路段会不会被判超速？(请通过计算进行说明)
(3)若要确保通过AB路段区间测速不会被判超速,则通过AB路段时间最短为多少秒？(请通过计算进行说明)

答案：
(1) 不会
(2) 会被判超速，计算见解析
(3) $ 750 \, \text{s} $，计算见解析
解析：
(1) 轿车通过监测点 $ A $、$ B $ 的速度分别为 $ 100 \, \text{km/h} $ 和 $ 110 \, \text{km/h} $，均小于 $ 120 \, \text{km/h} $，所以不会被判超速。
(2) 由图可知，从 $ A $ 运动到 $ B $ 的时间为 $ t = 10 \, \text{min} = \frac{1}{6} \, \text{h} $，$ v = \frac{s}{t} = \frac{25 \, \text{km}}{\frac{1}{6} \, \text{h}} = 150 \, \text{km/h} $，因为 $ 150 \, \text{km/h} ＞ 120 \, \text{km/h} $，所以这辆轿车会被判超速。
(3) 根据 $ v = \frac{s}{t} $ 可知，通过 $ AB $ 路段时间最短为 $ t_1 = \frac{s}{v} = \frac{25 \, \text{km}}{120 \, \text{km/h}} = \frac{5}{24} \, \text{h} = 750 \, \text{s} $。

16. 在一个长1 020 m注满水的铸铁水管的一端敲一下,在另一端听到三次声音,第一次声音同第二次声音间隔0.48 s,第二次声音与第三次声音间隔2.32 s,已知当时声音在空气中的传播速度为340 m/s,则声音通过空气从管子的一端传到另一端需要的时间为______s,声音通过水从管子的一端传到另一端需要的时间为______s,声音通过铸铁从管子的一端传到另一端需要的时间为______s,声音在铸铁中的传播速度为______m/s。

答案： $ 3 $ $ 0.68 $ $ 0.2 $ $ 5100 $ 解析：三次敲击声分别是通过空气、水、铁管传播的，因为声音在空气中传播速度小于在水中传播速度，在水中传播速度小于在铁中传播速度，所以第一声是通过铁管传播的，第二声是通过水传播的，第三声是通过空气传播的。声音通过空气从管子的一端传到另一端需要的时间为 $ t_{\text{空气}} = \frac{s}{v_{\text{空气}}} = \frac{1020 \, \text{m}}{340 \, \text{m/s}} = 3 \, \text{s} $。声音通过水从管子的一端传到另一端需要的时间 $ t_{\text{水}} = t_{\text{空气}} - \Delta t = 3 \, \text{s} - 2.32 \, \text{s} = 0.68 \, \text{s} $。声音通过铸铁从管子的一端传到另一端需要的时间为 $ t_{\text{铁}} = t_{\text{水}} - \Delta t' = 0.68 \, \text{s} - 0.48 \, \text{s} = 0.2 \, \text{s} $。声音在铸铁中的传播速度为 $ v_{\text{铁}} = \frac{s}{t_{\text{铁}}} = \frac{1020 \, \text{m}}{0.2 \, \text{s}} = 5100 \, \text{m/s} $。

17. 新素材 创新装置 光速的测定在物理学中有多种方法,迈克尔逊曾用类似于下述方法在地球上较精确地测定了光速。将激光发射器和接收装置按图示位置固定,装置a是四个侧面均镀有高反光涂层的正方体,可绕固定的中心轴转动(图示为俯视图),当正方体转动到图示位置静止时,激光束恰能以45°角照射到某侧面中心P点处,反射到相距几十公里外的一个山顶上,经此处的光反射器(内部结构未画出,不计光在其中的传播时间)反射后,平行于原光线射到正方体另一侧面中心Q点处,最终被接收装置接收到。

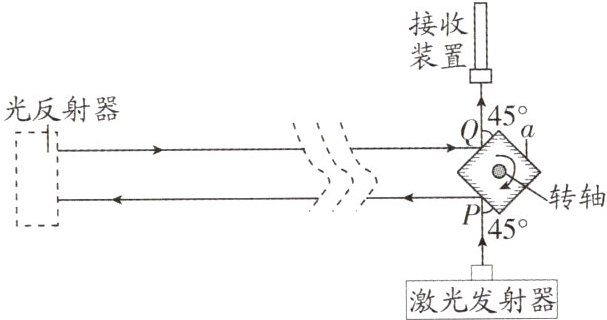
(1)若光速为$3×10^5 km/s,$正方体到光反射器之间的距离为30 km,则光从P点射出到射回Q点所用的时间为______s。
(2)当正方体的转速为n圈/秒时,接收装置可接收到激光,正方体与对面山顶光反射器间距离为30 km,则测得的光速最大为______m/s。

答案：
(1) $ 2 \times 10^{-4} $
(2) $ 2.4n \times 10^5 $
解析：
(1) 此处的光反射器，不计光在其中的传播时间，那么光从 $ P $ 点射出到射回 $ Q $ 点所走的路程为 $ 60 \, \text{km} $，光速为 $ 3 \times 10^5 \, \text{km/s} $，根据 $ t = \frac{s}{v} $ 可知，该过程所用的时间为 $ t = \frac{s}{v} = \frac{60 \, \text{km}}{3 \times 10^5 \, \text{km/s}} = 2 \times 10^{-4} \, \text{s} $，光从 $ P $ 点射出到射回 $ Q $ 点所用的时间为 $ 2 \times 10^{-4} \, \text{s} $。
(2) 如果要接收装置可接收到激光，那么需要正方体转 $ \frac{1}{4} $ 周的时间和光从 $ P $ 点射出到射回 $ Q $ 点所用的时间相同，当正方体的转速为 $ n $ 圈/秒时，转动周期为 $ \frac{1}{n} \, \text{s} $，转动一圈的时间为 $ \frac{1}{n} \, \text{s} $，那么转过 $ \frac{1}{4} $ 周的时间为 $ \frac{1}{4n} \, \text{s} $，此时光速最大，光从 $ P $ 点射出到射回 $ Q $ 点所用的时间为 $ t' = \frac{s}{v'} = \frac{60 \, \text{km}}{c} $，则 $ \frac{60 \, \text{km}}{c} = \frac{1}{4n} \, \text{s} $，解得 $ c = 2.4n \times 10^5 \, \text{m/s} $。