第119页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
13. 元旦期间小明和爸爸乘坐高铁去西安,他们乘坐的高铁列车长为420m,途中列车匀速经过一处长为2100m的隧道,小明坐在座位上测得自己从刚进隧道到出隧道口所用的时间为30s.求:
(1)高铁列车在隧道中的运行速度为多少?
(2)高铁列车完全通过隧道需要多少时间?
(3)高铁列车出隧道后速度保持不变,不久后恰与一列长约500m的普快列车同向并列行驶,小明从自己的座位与普快列车尾齐平时开始计数,直到自己的座位与普快列车头齐平时,他的动脉共跳动了15次,之后他测得自己的动脉每分钟跳动约75次.请你据此计算普快列车运行的平均速度约为多少km/h?
(1)高铁列车在隧道中的运行速度为多少?
(2)高铁列车完全通过隧道需要多少时间?
(3)高铁列车出隧道后速度保持不变,不久后恰与一列长约500m的普快列车同向并列行驶,小明从自己的座位与普快列车尾齐平时开始计数,直到自己的座位与普快列车头齐平时,他的动脉共跳动了15次,之后他测得自己的动脉每分钟跳动约75次.请你据此计算普快列车运行的平均速度约为多少km/h?
答案:
(1) $ 70 \, \text{m/s} $
(2) $ 36 \, \text{s} $
(3) $ 102 \, \text{km/h} $
解析:
(1)高铁列车在隧道中的运行速度为
$ v = \frac{s}{t} = \frac{2100 \, \text{m}}{30 \, \text{s}} = 70 \, \text{m/s} $.
(2)高铁列车完全通过隧道需要的时间
$ t' = \frac{s'}{v} = \frac{420 \, \text{m} + 2100 \, \text{m}}{70 \, \text{m/s}} = 36 \, \text{s} $.
(3)小明动脉每分钟跳动 $ 75 $ 次,则动脉跳动 $ 15 $ 次需要的时间
$ t'' = \frac{60 \, \text{s}}{75} \times 15 = 12 \, \text{s} $,
$ 12 \, \text{s} $ 的时间小明坐的高铁列车行驶的距离
$ s'' = vt'' = 70 \, \text{m/s} \times 12 \, \text{s} = 840 \, \text{m} $,
$ 12 \, \text{s} $ 内高铁比普快列车多行驶的路程,恰为普快列车的车长,则普快列车 $ 12 \, \text{s} $ 行驶的路程
$ s_{\text{普}} = s'' - s_{\text{普车}} = 840 \, \text{m} - 500 \, \text{m} = 340 \, \text{m} $,
普快列车运行的平均速度
$ v_{\text{普}} = \frac{s_{\text{普}}}{t''} = \frac{340 \, \text{m}}{12 \, \text{s}} = \frac{0.34 \, \text{km}}{\frac{12}{3600} \, \text{h}} = 102 \, \text{km/h} $.
(1) $ 70 \, \text{m/s} $
(2) $ 36 \, \text{s} $
(3) $ 102 \, \text{km/h} $
解析:
(1)高铁列车在隧道中的运行速度为
$ v = \frac{s}{t} = \frac{2100 \, \text{m}}{30 \, \text{s}} = 70 \, \text{m/s} $.
(2)高铁列车完全通过隧道需要的时间
$ t' = \frac{s'}{v} = \frac{420 \, \text{m} + 2100 \, \text{m}}{70 \, \text{m/s}} = 36 \, \text{s} $.
(3)小明动脉每分钟跳动 $ 75 $ 次,则动脉跳动 $ 15 $ 次需要的时间
$ t'' = \frac{60 \, \text{s}}{75} \times 15 = 12 \, \text{s} $,
$ 12 \, \text{s} $ 的时间小明坐的高铁列车行驶的距离
$ s'' = vt'' = 70 \, \text{m/s} \times 12 \, \text{s} = 840 \, \text{m} $,
$ 12 \, \text{s} $ 内高铁比普快列车多行驶的路程,恰为普快列车的车长,则普快列车 $ 12 \, \text{s} $ 行驶的路程
$ s_{\text{普}} = s'' - s_{\text{普车}} = 840 \, \text{m} - 500 \, \text{m} = 340 \, \text{m} $,
普快列车运行的平均速度
$ v_{\text{普}} = \frac{s_{\text{普}}}{t''} = \frac{340 \, \text{m}}{12 \, \text{s}} = \frac{0.34 \, \text{km}}{\frac{12}{3600} \, \text{h}} = 102 \, \text{km/h} $.
14. 核心素养 科学思维 如图,A是一辆装有超声测速装置的警车,正匀速行驶在一平直的公路上,某时刻向停在前方540m处的大卡车发射第一个超声波信号,经过3s接收到反射回来的信号,已知超声波的传播速度为340m/s,警车的行驶速度是____m/s.不久后有一辆小车刚好超越警车,5s之后警车发出第二个信号,并在0.51s之后收到小车反射回来的信号,小车的速度是____m/s.(设警车和小车的速度都保持不变,第二空结果保留一位小数)


答案:
$ 20 $ $ 36.4 $ 解析:由 $ v = \frac{s}{t} $ 得,从警车发射到接收到信号超声波移动的距离为 $ s_1 = v_{\text{声}} t_1 = 340 \, \text{m/s} \times 3 \, \text{s} = 1020 \, \text{m} $,
则警车移动的距离为 $ s_2 = 2s - s_1 = 2 \times 540 \, \text{m} - 1020 \, \text{m} = 60 \, \text{m} $,
则警车的速度为 $ v_{\text{警车}} = \frac{s_2}{t_1} = \frac{60 \, \text{m}}{3 \, \text{s}} = 20 \, \text{m/s} $.
警车发出第二个信号到接收到信号时间为 $ 0.51 \, \text{s} $,从警车发出信号到信号到达小车,超声波通过的路程 $ s_{\text{和}} = \frac{s_{\text{警车}} + s_{\text{声}}}{2} = \frac{v_{\text{警车}} t + v_{\text{声}} t}{2} = \frac{20 \, \text{m/s} \times 0.51 \, \text{s} + 340 \, \text{m/s} \times 0.51 \, \text{s}}{2} = 91.8 \, \text{m} $,
超声波通过这段路程所用的时间为 $ t_{\text{声}} = \frac{s_{\text{和}}}{v_{\text{声}}} = \frac{91.8 \, \text{m}}{340 \, \text{m/s}} = 0.27 \, \text{s} $,
小车从警车发出信号到信号到达小车又行驶了 $ 0.27 \, \text{s} $,则小车的速度为 $ v_{\text{车}} = \frac{s'}{t_{\text{声}}} $,
即 $ v_{\text{车}} = \frac{s'}{0.27 \, \text{s}} \cdots ① $,
小车在 $ 0.27 \, \text{s} $ 内移动的距离为 $ s' = s_{\text{和}} - v_{\text{车}} t + v_{\text{警车}} t $,即 $ s' = 91.8 \, \text{m} - v_{\text{车}} \times 5 \, \text{s} + 20 \, \text{m/s} \times 5 \, \text{s} \cdots ② $,
由①和②解得 $ v_{\text{车}} \approx 36.4 \, \text{m/s} $.
则警车移动的距离为 $ s_2 = 2s - s_1 = 2 \times 540 \, \text{m} - 1020 \, \text{m} = 60 \, \text{m} $,
则警车的速度为 $ v_{\text{警车}} = \frac{s_2}{t_1} = \frac{60 \, \text{m}}{3 \, \text{s}} = 20 \, \text{m/s} $.
警车发出第二个信号到接收到信号时间为 $ 0.51 \, \text{s} $,从警车发出信号到信号到达小车,超声波通过的路程 $ s_{\text{和}} = \frac{s_{\text{警车}} + s_{\text{声}}}{2} = \frac{v_{\text{警车}} t + v_{\text{声}} t}{2} = \frac{20 \, \text{m/s} \times 0.51 \, \text{s} + 340 \, \text{m/s} \times 0.51 \, \text{s}}{2} = 91.8 \, \text{m} $,
超声波通过这段路程所用的时间为 $ t_{\text{声}} = \frac{s_{\text{和}}}{v_{\text{声}}} = \frac{91.8 \, \text{m}}{340 \, \text{m/s}} = 0.27 \, \text{s} $,
小车从警车发出信号到信号到达小车又行驶了 $ 0.27 \, \text{s} $,则小车的速度为 $ v_{\text{车}} = \frac{s'}{t_{\text{声}}} $,
即 $ v_{\text{车}} = \frac{s'}{0.27 \, \text{s}} \cdots ① $,
小车在 $ 0.27 \, \text{s} $ 内移动的距离为 $ s' = s_{\text{和}} - v_{\text{车}} t + v_{\text{警车}} t $,即 $ s' = 91.8 \, \text{m} - v_{\text{车}} \times 5 \, \text{s} + 20 \, \text{m/s} \times 5 \, \text{s} \cdots ② $,
由①和②解得 $ v_{\text{车}} \approx 36.4 \, \text{m/s} $.
15. 有一圆形跑道,跑道长120m,甲、乙同学沿跑道同时同地反向匀速跑步时,每隔20s相遇一次,已知甲、乙速度之比为2:3,则甲的速度为____m/s,如果甲、乙同学以原速度沿跑道同时同地同向跑步,每隔____s相遇一次.
答案:
$ 2.4 $ $ 100 $ 解析:设甲的速度为 $ v_{\text{甲}} $,甲、乙速度之比为 $ 2 : 3 $,故乙的速度为 $ 1.5v_{\text{甲}} $,甲、乙同学沿跑道同时同地反向匀速跑步时,每隔 $ 20 \, \text{s} $ 相遇一次,则有 $ s_{\text{甲}} + s_{\text{乙}} = 120 \, \text{m} $,
即 $ v_{\text{甲}} t + v_{\text{乙}} t = 120 \, \text{m} $,
代入数值得 $ v_{\text{甲}} \times 20 \, \text{s} + 1.5v_{\text{甲}} \times 20 \, \text{s} = 120 \, \text{m} $,解得 $ v_{\text{甲}} = 2.4 \, \text{m/s} $, $ v_{\text{乙}} = 1.5 \times 2.4 \, \text{m/s} = 3.6 \, \text{m/s} $.
如果甲、乙同学以原速度沿跑道同时同地同向跑步,相遇时有 $ s'_{\text{乙}} - s'_{\text{甲}} = 120 \, \text{m} $,
则有 $ v_{\text{乙}} t' - v_{\text{甲}} t' = 120 \, \text{m} $,代入数值得 $ 3.6 \, \text{m/s} \times t' - 2.4 \, \text{m/s} \times t' = 120 \, \text{m} $,解得 $ t' = 100 \, \text{s} $.
即 $ v_{\text{甲}} t + v_{\text{乙}} t = 120 \, \text{m} $,
代入数值得 $ v_{\text{甲}} \times 20 \, \text{s} + 1.5v_{\text{甲}} \times 20 \, \text{s} = 120 \, \text{m} $,解得 $ v_{\text{甲}} = 2.4 \, \text{m/s} $, $ v_{\text{乙}} = 1.5 \times 2.4 \, \text{m/s} = 3.6 \, \text{m/s} $.
如果甲、乙同学以原速度沿跑道同时同地同向跑步,相遇时有 $ s'_{\text{乙}} - s'_{\text{甲}} = 120 \, \text{m} $,
则有 $ v_{\text{乙}} t' - v_{\text{甲}} t' = 120 \, \text{m} $,代入数值得 $ 3.6 \, \text{m/s} \times t' - 2.4 \, \text{m/s} \times t' = 120 \, \text{m} $,解得 $ t' = 100 \, \text{s} $.
16. 如图甲所示,小车A和小车B在马路上相向而行,小车A向右运动,小车B向左运动.如图乙是小车A和小车B的路程随着时间变化的坐标图,从开始计时到第16s两车正好相遇.
(1)小车A的速度是多少?
(2)如图乙所示,小车A和小车B在开始计时的时候相距多远?
(3)如图丙所示,马路为双向两车道,每一条道均为3.5m宽,以5m/s速度做匀速直线运动的小车C正前方25m处一行人正开始横穿马路,行人也做匀速直线运动,小车车长为5m(小车可看成一个长方体),小车C始终行驶在该车道的中间;为了能够安全通过,行人速度v的范围是多少?
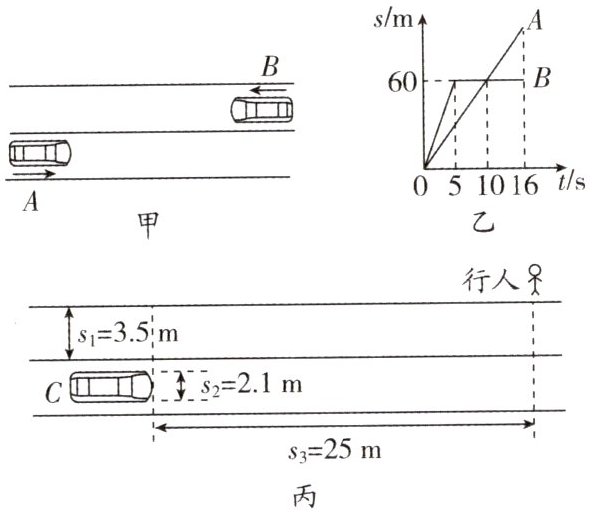
(1)小车A的速度是多少?
(2)如图乙所示,小车A和小车B在开始计时的时候相距多远?
(3)如图丙所示,马路为双向两车道,每一条道均为3.5m宽,以5m/s速度做匀速直线运动的小车C正前方25m处一行人正开始横穿马路,行人也做匀速直线运动,小车车长为5m(小车可看成一个长方体),小车C始终行驶在该车道的中间;为了能够安全通过,行人速度v的范围是多少?

答案:
(1) $ 6 \, \text{m/s} $
(2) $ 156 \, \text{m} $
(3)小于 $ 0.7 \, \text{m/s} $ 或大于 $ 1.26 \, \text{m/s} $
解析:
(1)由图乙可知,当小车 $ A $ 所走的路程为 $ 60 \, \text{m} $ 时,所用的时间为 $ 10 \, \text{s} $,小车 $ A $ 的运动图像为一条过原点的直线,小车 $ A $ 做匀速直线运动,它的速度为
$ v_A = \frac{s_A}{t_A} = \frac{60 \, \text{m}}{10 \, \text{s}} = 6 \, \text{m/s} $.
(2)由图乙可知, $ B $ 车 $ 16 \, \text{s} $ 总共运动的路程为 $ s_B = 60 \, \text{m} $,再根据速度公式 $ v = \frac{s}{t} $,可得 $ A $ 车 $ 16 \, \text{s} $ 总共运动的路程为
$ s'_A = v_A t'_A = 6 \, \text{m/s} \times 16 \, \text{s} = 96 \, \text{m} $,
则小车 $ A $ 和小车 $ B $ 在开始计时的时候相距的路程为
$ s = s'_A + s_B = 96 \, \text{m} + 60 \, \text{m} = 156 \, \text{m} $.
(3)由图丙可知,行人到小车的距离为
$ s_{\text{行人}} = s_1 + \frac{1}{2} \times (s_1 - s_2) = 3.5 \, \text{m} + \frac{1}{2} \times (3.5 \, \text{m} - 2.1 \, \text{m}) = 4.2 \, \text{m} $,
行人到达小车位置并且刚好经过小车的距离为
$ s'_{\text{行人}} = s_{\text{行人}} + s_2 = 4.2 \, \text{m} + 2.1 \, \text{m} = 6.3 \, \text{m} $,
小车刚好通过行人的直线走位,所用时间为 $ t_1 = \frac{s_3 + s_{\text{车}}}{v_{\text{车}}} = \frac{25 \, \text{m} + 5 \, \text{m}}{5 \, \text{m/s}} = 6 \, \text{s} $,
同时,假设行人刚好到达小车上边边沿的位置,那么该情况下,行人的步行速度为 $ v_{\text{行人}1} = \frac{s_{\text{行人}}}{t_1} = \frac{4.2 \, \text{m}}{6 \, \text{s}} = 0.7 \, \text{m/s} $,
当行人刚好到达小车下边边沿的位置时,假设小车刚好到达行人的直线走位,小车所用时间为
$ t_2 = \frac{s_3}{v_{\text{车}}} = \frac{25 \, \text{m}}{5 \, \text{m/s}} = 5 \, \text{s} $,
行人这个过程所用的时间大小等于小车所用的时间,则行人的速度为 $ v_{\text{行人}2} = \frac{s'_{\text{行人}}}{t_2} = \frac{6.3 \, \text{m}}{5 \, \text{s}} = 1.26 \, \text{m/s} $,
综上所述,行人速度 $ v $ 可以是小于 $ 0.7 \, \text{m/s} $,此时小车通过了,行人还没到达小车上边边沿的位置;或者也可以大于 $ 1.26 \, \text{m/s} $,此时小车刚好到达行人的直线走位时,行人已经过小车下边边沿位置,则行人速度 $ v $ 的范围是小于 $ 0.7 \, \text{m/s} $ 或大于 $ 1.26 \, \text{m/s} $.
(1) $ 6 \, \text{m/s} $
(2) $ 156 \, \text{m} $
(3)小于 $ 0.7 \, \text{m/s} $ 或大于 $ 1.26 \, \text{m/s} $
解析:
(1)由图乙可知,当小车 $ A $ 所走的路程为 $ 60 \, \text{m} $ 时,所用的时间为 $ 10 \, \text{s} $,小车 $ A $ 的运动图像为一条过原点的直线,小车 $ A $ 做匀速直线运动,它的速度为
$ v_A = \frac{s_A}{t_A} = \frac{60 \, \text{m}}{10 \, \text{s}} = 6 \, \text{m/s} $.
(2)由图乙可知, $ B $ 车 $ 16 \, \text{s} $ 总共运动的路程为 $ s_B = 60 \, \text{m} $,再根据速度公式 $ v = \frac{s}{t} $,可得 $ A $ 车 $ 16 \, \text{s} $ 总共运动的路程为
$ s'_A = v_A t'_A = 6 \, \text{m/s} \times 16 \, \text{s} = 96 \, \text{m} $,
则小车 $ A $ 和小车 $ B $ 在开始计时的时候相距的路程为
$ s = s'_A + s_B = 96 \, \text{m} + 60 \, \text{m} = 156 \, \text{m} $.
(3)由图丙可知,行人到小车的距离为
$ s_{\text{行人}} = s_1 + \frac{1}{2} \times (s_1 - s_2) = 3.5 \, \text{m} + \frac{1}{2} \times (3.5 \, \text{m} - 2.1 \, \text{m}) = 4.2 \, \text{m} $,
行人到达小车位置并且刚好经过小车的距离为
$ s'_{\text{行人}} = s_{\text{行人}} + s_2 = 4.2 \, \text{m} + 2.1 \, \text{m} = 6.3 \, \text{m} $,
小车刚好通过行人的直线走位,所用时间为 $ t_1 = \frac{s_3 + s_{\text{车}}}{v_{\text{车}}} = \frac{25 \, \text{m} + 5 \, \text{m}}{5 \, \text{m/s}} = 6 \, \text{s} $,
同时,假设行人刚好到达小车上边边沿的位置,那么该情况下,行人的步行速度为 $ v_{\text{行人}1} = \frac{s_{\text{行人}}}{t_1} = \frac{4.2 \, \text{m}}{6 \, \text{s}} = 0.7 \, \text{m/s} $,
当行人刚好到达小车下边边沿的位置时,假设小车刚好到达行人的直线走位,小车所用时间为
$ t_2 = \frac{s_3}{v_{\text{车}}} = \frac{25 \, \text{m}}{5 \, \text{m/s}} = 5 \, \text{s} $,
行人这个过程所用的时间大小等于小车所用的时间,则行人的速度为 $ v_{\text{行人}2} = \frac{s'_{\text{行人}}}{t_2} = \frac{6.3 \, \text{m}}{5 \, \text{s}} = 1.26 \, \text{m/s} $,
综上所述,行人速度 $ v $ 可以是小于 $ 0.7 \, \text{m/s} $,此时小车通过了,行人还没到达小车上边边沿的位置;或者也可以大于 $ 1.26 \, \text{m/s} $,此时小车刚好到达行人的直线走位时,行人已经过小车下边边沿位置,则行人速度 $ v $ 的范围是小于 $ 0.7 \, \text{m/s} $ 或大于 $ 1.26 \, \text{m/s} $.
查看更多完整答案,请扫码查看


