第116页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
15. 核心素养 物理观念 如表所示,是一款运动软件记录的某跑步者的部分跑步数据.
|运动路程:6.60 千米|
|----|
|平均配速:6 分 40 秒/千米|
|步数:7 500 步|
(1)由上表中信息可知,该跑步者的“步幅”(每步距离)为多少米?
(2)该跑步者全程的平均速度为多少?
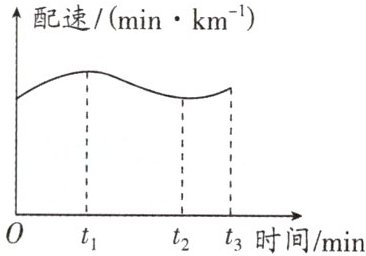
(3)若此次“配速”随时间变化的图像如图所示,请判断在 $ t_1 $、$ t_2 $ 和 $ t_3 $ 三个时刻中哪一时刻运动得最快? 作出简要说明.
(4)平均步频(即每分钟的步数)也是跑步的重要指标之一,该跑步者此次运动的平均步频为多少?(精确到个位)
|运动路程:6.60 千米|
|----|
|平均配速:6 分 40 秒/千米|
|步数:7 500 步|
(1)由上表中信息可知,该跑步者的“步幅”(每步距离)为多少米?
(2)该跑步者全程的平均速度为多少?
(3)若此次“配速”随时间变化的图像如图所示,请判断在 $ t_1 $、$ t_2 $ 和 $ t_3 $ 三个时刻中哪一时刻运动得最快? 作出简要说明.
(4)平均步频(即每分钟的步数)也是跑步的重要指标之一,该跑步者此次运动的平均步频为多少?(精确到个位)

答案:
(1)0.88 m
(2)2.5 m/s
(3)$t_{2},t_{2}$时刻配速最小,表示该跑步者通过相同的路程所用的时间最少,运动得最快
(4)170步/min
解析:
(1)跑步者的“步幅”(每步距离):$s_{0}=\frac {s}{n}=$
$\frac {6.6×10^{3}m}{7500}=0.88m$.
(2)该跑步者全程的平均配速为6 min 40 s,即400 s,则该跑步者平均每1 km需跑400 s,
故全程的平均速度为:$v=\frac {s}{t}=\frac {1000m}{400s}=2.5m/s$.
(3)$t_{2}$时刻运动得最快,因为$t_{2}$时刻配速最小,表示物体在相同的路程所用的时间最少,运动得最快.
(4)该跑者平均每1 km需跑400 s,全程为6.60 km,故全程时间为:$t=400s×6.60=2640s=44min$,总步数为7 500步,故平均步频为:$\frac {7500步}{44min}\approx 170步/min$.
(1)0.88 m
(2)2.5 m/s
(3)$t_{2},t_{2}$时刻配速最小,表示该跑步者通过相同的路程所用的时间最少,运动得最快
(4)170步/min
解析:
(1)跑步者的“步幅”(每步距离):$s_{0}=\frac {s}{n}=$
$\frac {6.6×10^{3}m}{7500}=0.88m$.
(2)该跑步者全程的平均配速为6 min 40 s,即400 s,则该跑步者平均每1 km需跑400 s,
故全程的平均速度为:$v=\frac {s}{t}=\frac {1000m}{400s}=2.5m/s$.
(3)$t_{2}$时刻运动得最快,因为$t_{2}$时刻配速最小,表示物体在相同的路程所用的时间最少,运动得最快.
(4)该跑者平均每1 km需跑400 s,全程为6.60 km,故全程时间为:$t=400s×6.60=2640s=44min$,总步数为7 500步,故平均步频为:$\frac {7500步}{44min}\approx 170步/min$.
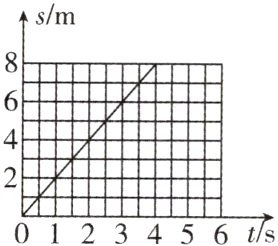
16. 甲、乙两小车沿同一直线同向而行,甲车的 $ s - t $ 图像如图所示.P、Q 是直线上的两点,当甲经过 P 点时,乙刚好经过 Q 点.已知 PQ 相距 5 m,再过 2 s,甲、乙两车相距 3 m,则乙车的速度可能是 ()
A. 2 m/s
B. 3 m/s
C. 4 m/s
D. 5 m/s

A. 2 m/s
B. 3 m/s
C. 4 m/s
D. 5 m/s
答案:
B 解析:由图像知,甲车做匀速直线运动,其速度$v_{甲}=$
$\frac {s_{甲}}{t_{甲}}=\frac {8m}{4s}=2m/s$,两车同向而行,若甲追乙,分别在P和Q点时,两车相距5 m,2 s后,两车相距3 m,说明甲比乙的速度快,则乙的速度小于2 m/s,没有符合的选项;若乙追甲,经2 s没有相遇,则甲通过的距离$s_{1}=v_{甲}t=2m/s×2s=$4 m,则乙通过的距离$s_{2}=s_{1}+s_{PQ}-Δs=4m+5m-3m=6m$,乙的速度$v_{乙}=\frac {s_{2}}{t}=\frac {6m}{2s}=3m/s$;乙追甲,相遇后继续行驶,相距3 m,乙通过的距离$s_{3}=s_{1}+s+Δs=4m+5m+3m=$12 m,乙的速度$v'_{乙}=\frac {s_{3}}{t}=\frac {12m}{2s}=6m/s$,故B符合题意,ACD不符合题意.故选B.
$\frac {s_{甲}}{t_{甲}}=\frac {8m}{4s}=2m/s$,两车同向而行,若甲追乙,分别在P和Q点时,两车相距5 m,2 s后,两车相距3 m,说明甲比乙的速度快,则乙的速度小于2 m/s,没有符合的选项;若乙追甲,经2 s没有相遇,则甲通过的距离$s_{1}=v_{甲}t=2m/s×2s=$4 m,则乙通过的距离$s_{2}=s_{1}+s_{PQ}-Δs=4m+5m-3m=6m$,乙的速度$v_{乙}=\frac {s_{2}}{t}=\frac {6m}{2s}=3m/s$;乙追甲,相遇后继续行驶,相距3 m,乙通过的距离$s_{3}=s_{1}+s+Δs=4m+5m+3m=$12 m,乙的速度$v'_{乙}=\frac {s_{3}}{t}=\frac {12m}{2s}=6m/s$,故B符合题意,ACD不符合题意.故选B.
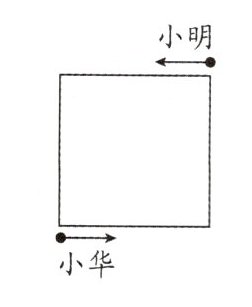
17. (2024·南通海安市期末)如图为某小区的正方形围墙,小明和小华紧贴围墙匀速行走一圈,需要的时间分别为 20 min 和 28 min,则小明和小华的速度之比为____.若小明和小华从围墙的两个对角处同时出发,沿逆时针方向紧贴围墙匀速行走,经过____min 两人第一次相遇;若小明和小华从围墙的两个对角处同时出发,从小明第一次看见小华开始计时,到小明又看不到小华时,所经历的时间为____min.

答案:
7:5 35 1 解析:小明和小华的速度之比$\frac {v_{明}}{v_{华}}=\frac {\frac {s_{明}}{t_{明}}}{\frac {s_{华}}{t_{华}}}=$
$\frac {s_{明}t_{华}}{t_{明}s_{华}}=\frac {28min}{20min}=\frac {7}{5}$,设绕墙一圈的路程为s,则小明的速度为$\frac {s}{20min}$,小华的速度为$\frac {s}{28min}$,设两人第一次相遇所需时间为t,则$s_{明}=s_{华}+\frac {s}{2}$,代入数据可知$\frac {s}{20min}t=\frac {s}{28min}t+\frac {s}{2}$,经整理可知$t=35min$;设正方形的边长为L,则小明走一个边长所需的时间为$t_{小明L}=\frac {20min}{4}=5min$,同理,小华走一个边长所需的时间为$t_{小华L}=\frac {28min}{4}=7min$.判断小明能否看见小华,即判断小明到达一个端点时,小华是否还在这条边上.小明走完三个边长时,共用时15 min,此时小华走了2L多一些,故小明看不见小华;当小明走完四个边长时,共用时20 min,此时小华走了3L不到的路程,故小明第一次看见小华.第21 min时,小华刚好拐弯,小明又看不见小华,故20~21 min这段时间内小明能看见小华,经历时间为1 min.
$\frac {s_{明}t_{华}}{t_{明}s_{华}}=\frac {28min}{20min}=\frac {7}{5}$,设绕墙一圈的路程为s,则小明的速度为$\frac {s}{20min}$,小华的速度为$\frac {s}{28min}$,设两人第一次相遇所需时间为t,则$s_{明}=s_{华}+\frac {s}{2}$,代入数据可知$\frac {s}{20min}t=\frac {s}{28min}t+\frac {s}{2}$,经整理可知$t=35min$;设正方形的边长为L,则小明走一个边长所需的时间为$t_{小明L}=\frac {20min}{4}=5min$,同理,小华走一个边长所需的时间为$t_{小华L}=\frac {28min}{4}=7min$.判断小明能否看见小华,即判断小明到达一个端点时,小华是否还在这条边上.小明走完三个边长时,共用时15 min,此时小华走了2L多一些,故小明看不见小华;当小明走完四个边长时,共用时20 min,此时小华走了3L不到的路程,故小明第一次看见小华.第21 min时,小华刚好拐弯,小明又看不见小华,故20~21 min这段时间内小明能看见小华,经历时间为1 min.
查看更多完整答案,请扫码查看


