《2025年经纶学典学霸题中题八年级物理上册苏科版》

1. 2023 年深圳马拉松于 12 月 3 日开赛, 比赛项目为男子组、女子组和团体赛, 马拉松以市民中心为起点, 海滨广场为终点, 全程 42 km, 一名选手用时 140 min 跑完全程. 求:
(1) 这名选手跑完马拉松的平均速度是多少米每秒?
(2) 参加马拉松的选手们从深南大道北侧西行到宝安大道, 此路段直线长度为 8.5 km, 马拉松团体队伍从进入该直线路段到全部通过此路段共用时 2 000 s, 队伍匀速前进的速度为 4.4 m/s, 请你求出马拉松团体队伍的长度.
视频讲解

答案：
(1) $ 5 \, \text{m/s} $
(2) $ 300 \, \text{m} $
解析:
(1) 由 $ 1 \, \text{min} = 60 \, \text{s} $ 得
$ t = 140 \, \text{min} = 140 \times 60 \, \text{s} = 8400 \, \text{s} $,
选手跑完马拉松的平均速度为
$ v = \frac{s}{t} = \frac{42000 \, \text{m}}{8400 \, \text{s}} = 5 \, \text{m/s} $.
(2) 由 $ v = \frac{s}{t} $ 得, 马拉松团体队伍通过的总路程为
$ s_{\text{总}} = v't' = 4.4 \, \text{m/s} \times 2000 \, \text{s} = 8800 \, \text{m} $,
所以, 队伍的长度
$ L = s_{\text{总}} - s_{\text{路}} = 8800 \, \text{m} - 8500 \, \text{m} = 300 \, \text{m} $.

2. 如今, 高铁极大地方便了人们的出行, 新中国成立 70 周年国庆假前, 小明选择从无锡东乘坐高铁去徐州东, 他通过铁路 12306 网站查询到 G12XX 次的运行时刻表如下. 他决定乘坐这趟车.

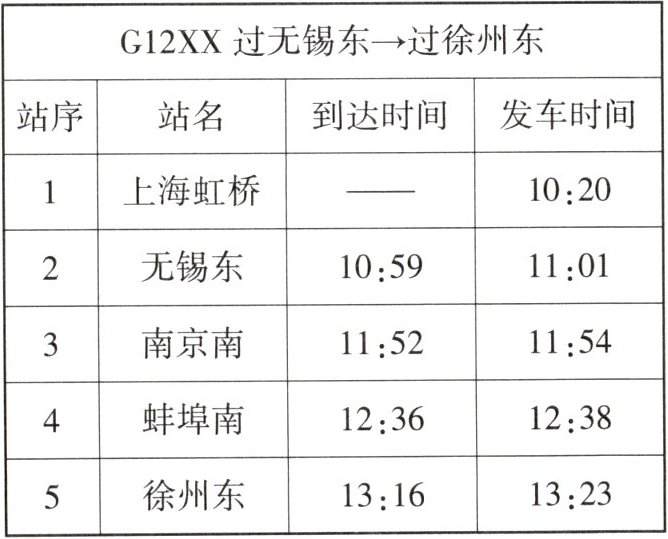
(1) 无锡东到徐州东的高铁里程为 495 km, 若该趟高铁按照时刻表, 从无锡东运行到徐州东, 则该趟高铁在此区间运行的平均速度是多大?
(2) 当该趟高铁途经南京大胜关长江大桥时, 车厢内速度显示为 252 km/h, 小明想估测大桥的长度, 设高铁匀速通过大桥.
① 当他所坐的位置到达桥头时, 用手机上的秒表功能开始计时, 所坐的位置驶出桥尾时, 秒表下方数字显示为 132 s, 则大桥长度为多少?
② 若该列车全长为 350 m, 列车全部在大桥上运行的时间为多少?

答案：
(1) $ 220 \, \text{km/h} $
(2) ① $ 9240 \, \text{m} $ ② $ 127 \, \text{s} $
解析:
(1) 从无锡东运行到徐州东的时间为 $ t = 13:16 - 11:01 = 2.25 \, \text{h} $, 则从无锡东运行到徐州东, 该趟高铁在此区间运行的平均速度为 $ v = \frac{s}{t} = \frac{495 \, \text{km}}{2.25 \, \text{h}} = 220 \, \text{km/h} $.
(2) ① 大桥长度为 $ l_1 = v_1 t_1 = 252 \, \text{km/h} \times 132 \, \text{s} = 70 \, \text{m/s} \times 132 \, \text{s} = 9240 \, \text{m} $.
② 列车全部在大桥上运行的时间为 $ t_2 = \frac{l_1 - l_{\text{车}}}{v_1} = \frac{9240 \, \text{m} - 350 \, \text{m}}{70 \, \text{m/s}} = 127 \, \text{s} $.

3. 小明从上高中就开始骑自行车去上学, 他家离学校 4 km, 他以 10 km/h 的速度骑车上学, 出发 9 min 后小明爸爸发现小明的语文教科书忘记带上, 立即以 20 km/h 的速度沿小明上学的方向骑车去追小明. 求:
(1) 小明爸爸经多少分钟能追上小明?
(2) 如果小明爸爸发现小明忘记带教科书的同时, 小明也发现自己的教科书忘记带上并立即掉头返回, 小明与爸爸在途中相遇时离学校多少千米?
视频讲解

答案：
(1) $ 9 \, \text{min} $
(2) $ 3 \, \text{km} $
解析:
(1) 若经过 $ t $ 小时爸爸能追上小明, 则此过程小明通过的路程 $ s_1 = v_1 (t_0 + t) $,
小明爸爸通过的路程与小明的相等, 即 $ s_2 = v_2 t = s_1 $,
则 $ v_1 (t_0 + t) = v_2 t $,
即 $ 10 \, \text{km/h} \times \left( 9 \times \frac{1}{60} \, \text{h} + t \right) = 20 \, \text{km/h} \times t $,
解得 $ t = 0.15 \, \text{h} = 9 \, \text{min} $.
(2) 出发 $ 9 \, \text{min} $, 小明通过的路程
$ s = v_1 t_0 = 10 \, \text{km/h} \times 9 \times \frac{1}{60} \, \text{h} = 1.5 \, \text{km} $,
小明与爸爸相向而行的相对速度
$ v = v_1 + v_2 = 10 \, \text{km/h} + 20 \, \text{km/h} = 30 \, \text{km/h} $,
则他们相遇的时间
$ t' = \frac{s}{v} = \frac{1.5 \, \text{km}}{30 \, \text{km/h}} = \frac{1}{20} \, \text{h} $,
因此小明爸爸通过的路程为
$ s_2' = v_2 t' = 20 \, \text{km/h} \times \frac{1}{20} \, \text{h} = 1 \, \text{km} $,
则他们相遇时, 与学校的距离为
$ s'' = s_{\text{总}} - s_2' = 4 \, \text{km} - 1 \, \text{km} = 3 \, \text{km} $.