2025年实验班提优训练暑假衔接版五升六年级数学北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年实验班提优训练暑假衔接版五升六年级数学北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第78页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
例1 八月用水多少吨?说说你是如何思考的?

九月比八月节约了$\frac {1}{7}$。
过程探索 根据“九月比八月节约了$\frac {1}{7}$”可知,应该把()看作单位“1”。
完全解答 先找到题目中的单位“1”,通常在“比”后面,再根据单位“1”和题意列出等量关系式,最后列方程解答。

九月比八月节约了$\frac {1}{7}$。
过程探索 根据“九月比八月节约了$\frac {1}{7}$”可知,应该把()看作单位“1”。
完全解答 先找到题目中的单位“1”,通常在“比”后面,再根据单位“1”和题意列出等量关系式,最后列方程解答。
答案:
八月的用水量
例2 你能找到等量关系吗?画一画,想一想。
过程探索 方法一:用方框图表示。以八月用水量为单位“1”,将八月用水量用7个方框表示,由“九月比八月节约了$\frac {1}{7}$”,可知九月用水量就是用()个方框表示。
方法二:用线段表示。将表示八月用水量的线段平均分为7小段,根据“九月比八月节约了$\frac {1}{7}$”,可知九月用水量就是用其中的()段小线段来表示。
完全解答 方法一:等量关系为八月的用水量一八月用水量的$\frac {1}{7}= $九月的用水量。如左下图。
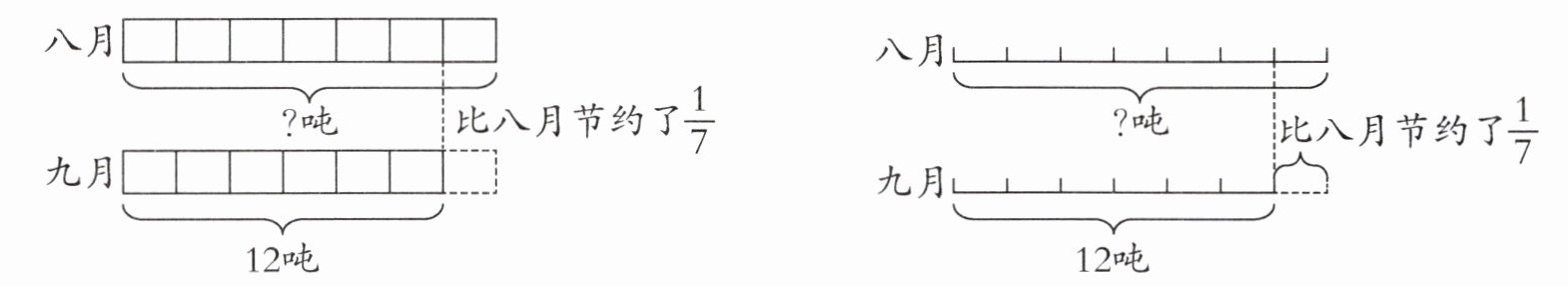
方法二:等量关系为八月的用水量$×(1-\frac {1}{7})= $九月的用水量。如右上图。
过程探索 方法一:用方框图表示。以八月用水量为单位“1”,将八月用水量用7个方框表示,由“九月比八月节约了$\frac {1}{7}$”,可知九月用水量就是用()个方框表示。
方法二:用线段表示。将表示八月用水量的线段平均分为7小段,根据“九月比八月节约了$\frac {1}{7}$”,可知九月用水量就是用其中的()段小线段来表示。
完全解答 方法一:等量关系为八月的用水量一八月用水量的$\frac {1}{7}= $九月的用水量。如左下图。
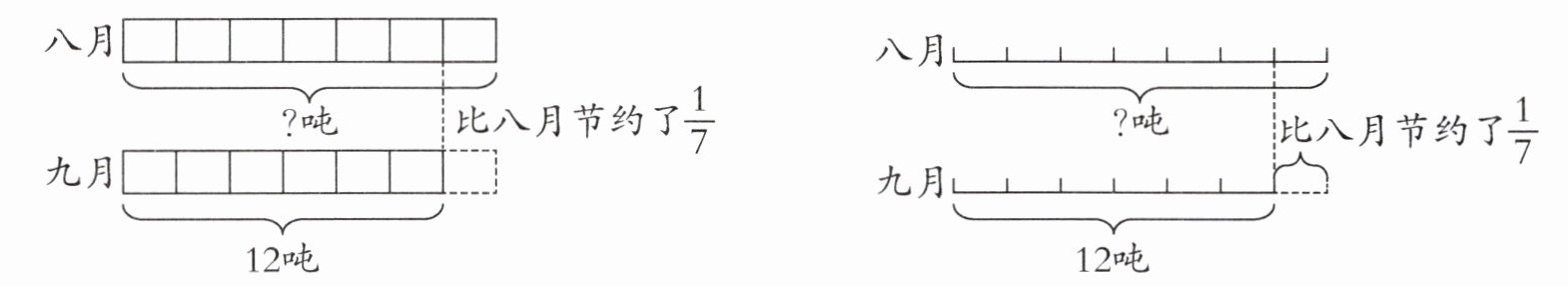
方法二:等量关系为八月的用水量$×(1-\frac {1}{7})= $九月的用水量。如右上图。
答案:
6 6
![img alt=例1例2]
![img alt=例1例2]
例3 列出方程,解决问题。
过程探索 已知九月用水量为12吨,且比八月用水量少$\frac {1}{7}$。方法一:用八月用水量减去九月比八月少的用水量,结果就是九月的用水量。方法二:先求出九月份用水量占八月用水量的分率,再用这个分率乘八月用水量,结果就是九月用水量。在列方程解答后别忘记检验。
完全解答 方法一:解:设八月用水$x$吨。
$x-\frac {1}{7}x= 12$ $x= 14$
方法二:解:设八月用水$x$吨。
$(1-\frac {1}{7})x= 12$ $x= 14$
答:八月用水14吨。
过程探索 已知九月用水量为12吨,且比八月用水量少$\frac {1}{7}$。方法一:用八月用水量减去九月比八月少的用水量,结果就是九月的用水量。方法二:先求出九月份用水量占八月用水量的分率,再用这个分率乘八月用水量,结果就是九月用水量。在列方程解答后别忘记检验。
完全解答 方法一:解:设八月用水$x$吨。
$x-\frac {1}{7}x= 12$ $x= 14$
方法二:解:设八月用水$x$吨。
$(1-\frac {1}{7})x= 12$ $x= 14$
答:八月用水14吨。
答案:
- 方法一:设八月用水$x$吨,因为九月比八月用水量少$\frac{1}{7}$,那么九月比八月少的用水量就是$\frac{1}{7}x$吨,用八月用水量$x$吨减去九月比八月少的用水量$\frac{1}{7}x$吨,就等于九月的用水量$12$吨,所以可列方程$x - \frac{1}{7}x = 12$,合并同类项得$\frac{6}{7}x = 12$,两边同时除以$\frac{6}{7}$,即$x = 12\div\frac{6}{7}=12\times\frac{7}{6}=14$吨。
- 方法二:设八月用水$x$吨,九月比八月用水量少$\frac{1}{7}$,那么九月份用水量占八月用水量的分率就是$1 - \frac{1}{7}=\frac{6}{7}$,用这个分率$\frac{6}{7}$乘八月用水量$x$吨,结果就是九月用水量$12$吨,所以可列方程$(1 - \frac{1}{7})x = 12$,即$\frac{6}{7}x = 12$,两边同时除以$\frac{6}{7}$,解得$x = 14$吨。
最后检验:把$x = 14$代入方程左边,方法一:$14-\frac{1}{7}\times14 = 14 - 2 = 12$,与方程右边相等;方法二:$(1 - \frac{1}{7})\times14=\frac{6}{7}\times14 = 12$,与方程右边相等,所以$x = 14$是方程的解。
八月用水$14$吨。
- 方法二:设八月用水$x$吨,九月比八月用水量少$\frac{1}{7}$,那么九月份用水量占八月用水量的分率就是$1 - \frac{1}{7}=\frac{6}{7}$,用这个分率$\frac{6}{7}$乘八月用水量$x$吨,结果就是九月用水量$12$吨,所以可列方程$(1 - \frac{1}{7})x = 12$,即$\frac{6}{7}x = 12$,两边同时除以$\frac{6}{7}$,解得$x = 14$吨。
最后检验:把$x = 14$代入方程左边,方法一:$14-\frac{1}{7}\times14 = 14 - 2 = 12$,与方程右边相等;方法二:$(1 - \frac{1}{7})\times14=\frac{6}{7}\times14 = 12$,与方程右边相等,所以$x = 14$是方程的解。
八月用水$14$吨。
查看更多完整答案,请扫码查看


