《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

17. (8分)已知二次函数$y = 2 x ^ { 2 } + 6 x + 3$,将其化为$y = a ( x - h ) ^ { 2 } + k$的形式,并写出顶点坐标.

答案： 将二次函数$y = 2x^{2}+6x + 3$化为$y = a(x - h)^{2}+k$的形式为$y=2(x + \frac{3}{2})^{2}-\frac{3}{2}$，顶点坐标为$(-\frac{3}{2},-\frac{3}{2})$。

18. (8分)已知二次函数$y = a x ^ { 2 } + b x + c ( a \neq 0 )$,自变量$x与函数值y$的部分对应值如下表.

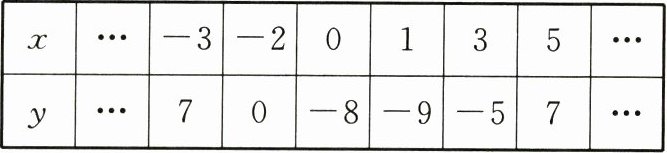
根据表格,回答下列问题:
(1)当$x = 2$时,$y = $____;
(2)求该二次函数的解析式.

答案：
(1) $-8$；
(2) $y = 3x^{2}+2x-8$。

19. (8分)已知二次函数$y = ( x - 1 ) ^ { 2 } - 4$.
(1)用列表描点法,在如图所示的平面直角坐标系中画出该二次函数的图象.

(2)根据图象回答:
①当$0 ＜ x \leqslant 3$时,$y$的取值范围是____;
②当$y ＜ 0$时,$x$的取值范围是____.

答案：
(1) 列表如上；
(2) ①$-4\leqslant y\leqslant0$；②$-1\lt x\lt3$。

20. (8分)已知抛物线$y = x ^ { 2 } - 1与直线y = 2 x + m有且只有一个交点A$,求$m的值以及交点A$的坐标.

答案： $m$的值为$-2$，交点$A$的坐标为$(1,0)$。