《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

24. (12分)在平面直角坐标系中,$M ( x _ { 1 } , y _ { 1 } )$,$N ( x _ { 2 } , y _ { 2 } )为抛物线y = a x ^ { 2 } + b x + c ( a ＞ 0 )$上任意两点,其中$x _ { 1 } ＜ x _ { 2 }$,设抛物线的对称轴为直线$x = t$.
(1)若$x _ { 2 } = 2$,$y _ { 2 } = c$,求$t$的值;
(2)若对于$x _ { 1 } + x _ { 2 } ＞ 3$,都有$y _ { 1 } ＜ y _ { 2 }$,求$t$的取值范围.

答案：
(1)$t$的值为$1$；
(2)$t$的取值范围是$t\leqslant\frac{3}{2}$。

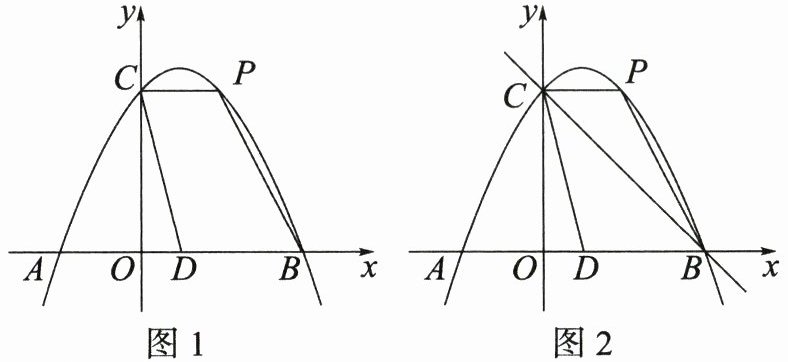
25. (14分)如图,在平面直角坐标系中,抛物线$y = a x ^ { 2 } + b x + 4 ( a \neq 0 )的对称轴是直线x = 1$,抛物线与$x轴交于点A$,$B$,与$y轴交于点C$,点$A的坐标是( - 2 , 0 )$.
(1)求抛物线的解析式;
(2)如图1,$P$是第一象限抛物线上的一个动点,点$D是抛物线的对称轴与x$轴的交点,连接$CD$,$CP$,$PB$,求四边形$PCDB$面积的最大值,并求出此时点$P$的坐标;
(3)如图2,在(2)的条件下,点$M是直线BC$上一点,当$\triangle POM是以OP$为腰的等腰三角形时,请直接写出点$M$的坐标.

答案： $(1)$抛物线解析式为$\boldsymbol{y=-\frac{1}{2}x^{2}+x + 4}$；
$(2)$四边形$PCDB$面积最大值为$\boldsymbol{14}$，此时$P$点坐标为$\boldsymbol{(2,4)}$；
$(3)$点$M$的坐标为$\boldsymbol{(2+\sqrt{6},2-\sqrt{6})}$，$\boldsymbol{(2-\sqrt{6},2+\sqrt{6})}$，$\boldsymbol{(-2,6)}$。