《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

23. (10分)阅读下列材料:
小明遇到了一个问题:5个同样大小的正方形纸片排列形式如图1所示,将它们分割后拼接成一个新的正方形.
他的做法是:按照图2所示的方法分割后,将三角形纸片ADO绕AB的中点O旋转至三角形纸片BEO处,依此法继续操作,即可拼接成一个新的正方形DEFG.
请你参考小明的做法解决下列问题:
(1)现有5个形状、大小相同的矩形纸片,排列形式如图3所示,请将其分割后拼接成一个平行四边形.要求:在图3中画出并指明拼接成的平行四边形(画出一个符合条件的平行四边形即可).
(2)如图4,在面积为$\sqrt {2}的//ogram ABCD$中,点E,F,G,H分别是边AB,BC,CD,DA的中点,分别连接AF,BG,CH,DE,得到一个新的$//ogram IJKL$.请在图4中探究$//ogram IJKL$面积的大小(画图并直接写出结果).

答案：
(1) 如图（分割拼接方法不唯一），拼接成的平行四边形为$□ABCD$（自行根据所画图形标注）。
(2) $//ogram IJKL$的面积为$\frac{\sqrt{2}}{5}$。

24. (12分)如图,在$△ABC$中,$∠BAC= 90^{\circ },AB= AC$,点P为$△ABC$内一点,连接AP,BP,CP,将线段AP绕点A逆时针旋转$90^{\circ }得到AP'$,连接$PP',CP'$.
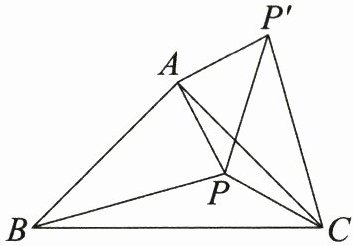
(1)用等式表示BP与$CP'$的数量关系,并证明.
(2)当$∠BPC= 135^{\circ }$时,
①$∠P'CP$的度数为____;
②若M为BC的中点,连接PM,请用等式表示PM与AP的数量关系,并证明.

答案：
(1) $BP = CP'$，证明如上。
(2) ①$90^{\circ}$；②$PM=\frac{\sqrt{2}}{2}AP$，证明如上。