24. (12分)阅读下列材料,并完成相应的任务.
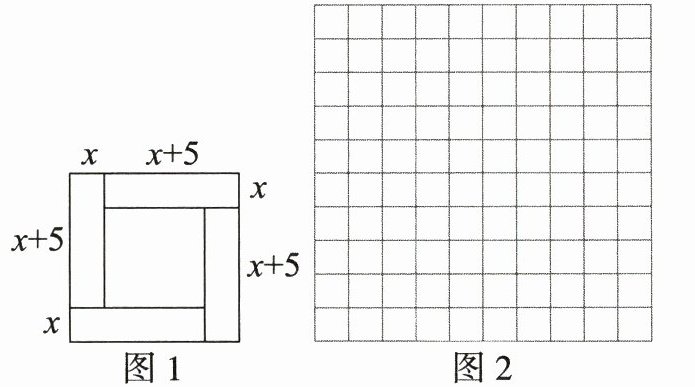
材料:一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中. 到了中世纪,阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法,并用几何法进行了证明. 我国古代三国时期的数学家赵爽也给出了类似的几何解法. 赵爽在其所著的《勾股圆方图注》中记载了解方程 $ x^{2} + 5x - 14 = 0 $,即 $ x(x + 5) = 14 $ 的方法. 首先构造了如图1所示的图形,图中的大正方形的面积是 $ (x + x + 5)^{2} $,其中四个全等的小矩形的面积均为 $ x(x + 5) = 14 $,中间的小正方形的面积为 $ 5^{2} $,所以大正方形的面积又可以表示为 $ 4 × 14 + 5^{2} $,据此易得原方程的正数解为 $ x = 2 $.
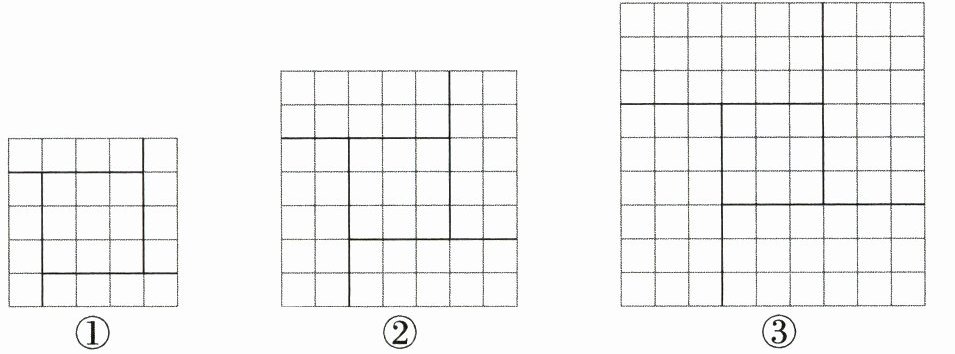
任务:(1)参照图解方程 $ x^{2} + 5x - 14 = 0 $ 的方法,下列三个构图中,能够说明方程 $ x^{2} - 3x - 10 = 0 $ 解法的是______(填序号).
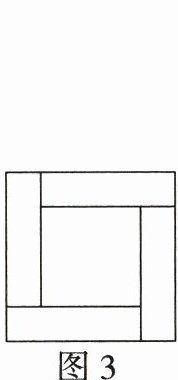
(2)在图2的网格中设计正确的构图,用几何法求出方程 $ x^{2} + 2x - 15 = 0 $ 的正数解(写出必要的思考过程,图2中的网格不要求全部使用).
(3)一般地,对于形如 $ x^{2} + ax = b $ 的一元二次方程,可以构造图3来解,图中的4个矩形全等. 若这4个矩形的总面积为20,中间围成的小正方形的边长为 $ \sqrt{5} $,则 $ a = $______,$ b = $______.
材料:一元二次方程及其解法最早出现在公元前两千年左右的古巴比伦人的《泥板文书》中. 到了中世纪,阿拉伯数学家花拉子米在他的代表作《代数学》中给出了一元二次方程的一般解法,并用几何法进行了证明. 我国古代三国时期的数学家赵爽也给出了类似的几何解法. 赵爽在其所著的《勾股圆方图注》中记载了解方程 $ x^{2} + 5x - 14 = 0 $,即 $ x(x + 5) = 14 $ 的方法. 首先构造了如图1所示的图形,图中的大正方形的面积是 $ (x + x + 5)^{2} $,其中四个全等的小矩形的面积均为 $ x(x + 5) = 14 $,中间的小正方形的面积为 $ 5^{2} $,所以大正方形的面积又可以表示为 $ 4 × 14 + 5^{2} $,据此易得原方程的正数解为 $ x = 2 $.


任务:(1)参照图解方程 $ x^{2} + 5x - 14 = 0 $ 的方法,下列三个构图中,能够说明方程 $ x^{2} - 3x - 10 = 0 $ 解法的是______(填序号).

(2)在图2的网格中设计正确的构图,用几何法求出方程 $ x^{2} + 2x - 15 = 0 $ 的正数解(写出必要的思考过程,图2中的网格不要求全部使用).
(3)一般地,对于形如 $ x^{2} + ax = b $ 的一元二次方程,可以构造图3来解,图中的4个矩形全等. 若这4个矩形的总面积为20,中间围成的小正方形的边长为 $ \sqrt{5} $,则 $ a = $______,$ b = $______.
答案:
$(1)$ $\boldsymbol{②}$;
$(2)$ 正数解为$\boldsymbol{3}$;
$(3)$ $a = \boldsymbol{2\sqrt{5}}$,$b = \boldsymbol{5}$。
$(2)$ 正数解为$\boldsymbol{3}$;
$(3)$ $a = \boldsymbol{2\sqrt{5}}$,$b = \boldsymbol{5}$。
查看更多完整答案,请扫码查看


