《2025年阳光同学分层设计九年级数学全一册人教版福建专版》

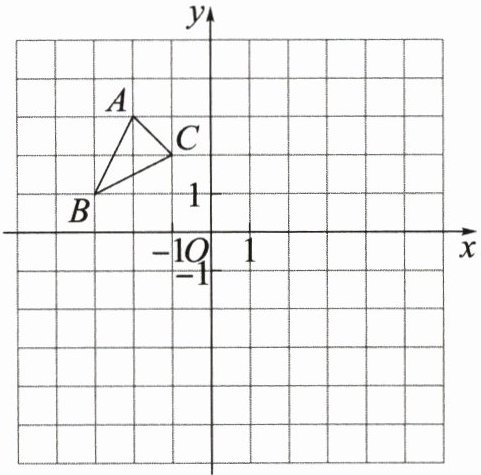
19. (8分)在平面直角坐标系中,$\triangle ABC$的位置如图所示.
(1)将$\triangle ABC$绕点O顺时针旋转$90^{\circ }得到\triangle A_{1}B_{1}C_{1}$,作出$\triangle A_{1}B_{1}C_{1}$,并写出点$C_{1}$的坐标;
(2)以原点O为位似中心,在第四象限内作出$\triangle ABC的位似图形\triangle A_{2}B_{2}C_{2}$,且$\triangle A_{2}B_{2}C_{2}与\triangle ABC$的相似比为2,并写出点$A_{2}$的坐标.

答案：
(1) 作出$\triangle A_{1}B_{1}C_{1}$（图略），点$C_{1}$的坐标为$(2,1)$。
(2) 作出$\triangle A_{2}B_{2}C_{2}$（图略），点$A_{2}$的坐标为$(4, - 6)$。

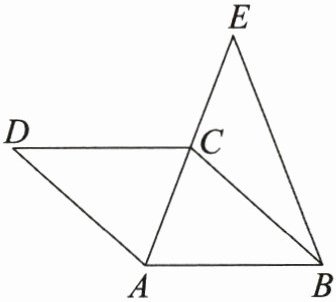
20. (8分)如图,四边形ABCD为菱形,点E在AC的延长线上,$∠ACD= ∠ABE$.求证:$\triangle ABC\backsim \triangle AEB$.

答案： 在菱形$ABCD$中，$AB = BC$，所以$\angle BAC=\angle BCA$。
因为$\angle ACD+\angle BCA = 180^{\circ}$，$\angle ABE+\angle AEB=180^{\circ}$，且$\angle ACD=\angle ABE$，所以$\angle BCA=\angle AEB$，进而$\angle BAC=\angle AEB$。
在$\triangle ABC$和$\triangle AEB$中，$\left\{\begin{array}{l}\angle BAC=\angle EAB\\\angle ACB=\angle AEB\end{array}\right.$，所以$\triangle ABC\backsim\triangle AEB$（两角分别相等的两个三角形相似）。

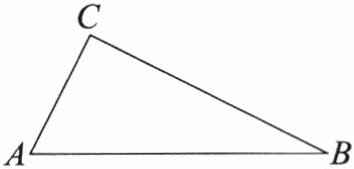
21. (8分)如图,已知$\triangle ABC$,请用尺规作图法在线段BC上找一点D,使$AC^{2}= CD\cdot CB$(保留作图痕迹,不写作法).

答案： 按照上述尺规作图方法作出$D$点（作图痕迹略），此时$D$点满足$AC^{2}=CD\cdot CB$。

22. (10分)如图,已知$\triangle ABC\backsim \triangle DEF$,求$\triangle ABC与\triangle DEF$的面积比.

答案： $\triangle ABC$与$\triangle DEF$的面积比为$\boldsymbol{\frac{a^{2}}{(b + c)^{2}}}$。