《2025年名校作业九年级数学下册北师大版》

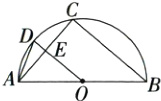
13. (本题10分)如图，AB是半圆O的直径，C，D是半圆O上的两点，且OD//BC，OD与AC相交于点E，连接AD.
(1)若$\angle ODA = 70^{\circ}$，求$\angle CAD$的度数；
(2)若AC = 8，DE = 2，求AB的长.

答案： 解:
(1)$\because AB$是半圆O的直径,
$\therefore\angle ACB = 90^{\circ}.$ (2分)
$\because OD// BC,$
$\therefore\angle AEO=\angle ACB = 90^{\circ}.$ (3分)
$\therefore\angle CAD=\angle AEO-\angle ODA = 90^{\circ}-70^{\circ}=20^{\circ}.$ (4分)
(2)设$OA = OD = x$,则$OE = OD - DE = x - 2,AB = 2x.$ (5分)
$\because\angle AEO = 90^{\circ},OD$是半圆O的半径,
$\therefore AE=\frac{1}{2}AC=\frac{1}{2}\times8 = 4.$ (7分)
在$Rt\triangle AEO$中,$AE^{2}+OE^{2}=OA^{2},$
即$4^{2}+(x - 2)^{2}=x^{2}$,解得$x = 5.$ (9分)
$\therefore AB = 10.$ (10分)

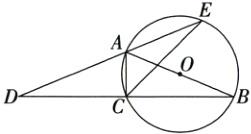
14. (本题10分)如图，AB为⊙O的直径，点C在⊙O上，连接BC并延长至点D，使CD = BC，连接DA并延长交⊙O于点E，连接AC，CE.
(1)求证：$\angle B=\angle D$.
(2)若AB = 13，AC = 5，求CE的长.

答案：
(1)证明:$\because AB$为$\odot O$的直径,
$\therefore\angle ACB = 90^{\circ}.\therefore AC\perp BD.$ (2分)
又$\because CD = BC,$
$\therefore AC$垂直平分BD. (3分)
$\therefore AD = AB.\therefore\angle B=\angle D.$ (4分)
(2)解:在$Rt\triangle ABC$中,$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{13^{2}-5^{2}}=12.$ (6分)
$\because\widehat{AC}=\widehat{AC},\therefore\angle B=\angle E.$ (8分)
又$\because\angle B=\angle D,$
$\therefore\angle D=\angle E.\therefore CD = CE.$ (9分)
$\because CD = BC,\therefore CE = BC = 12.$ (10分)

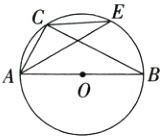
15. (本题13分)如图，AB是⊙O的直径，点C在⊙O上，AC = 6，点E是$\widehat{BC}$上一点，且$\sin\angle AEC=\frac{3}{5}$，连接BC.
(1)求AB的长；
(2)若点E为$\widehat{BC}$的中点，求CE的长.

答案：
解:
(1)$\because AB$为$\odot O$的直径,
$\therefore\angle ACB = 90^{\circ}.$ (2分)
$\because\widehat{AC}=\widehat{AC},\therefore\angle ABC=\angle AEC.$ (4分)
$\therefore\sin\angle ABC=\sin\angle AEC.$
$\therefore\frac{AC}{AB}=\frac{3}{5}.$ (5分)
$\because AC = 6,\therefore AB = 10.$ (6分)
(2)如图,连接OE交BC于点P.

在$Rt\triangle ABC$中,$BC=\sqrt{AB^{2}-AC^{2}}=\sqrt{10^{2}-6^{2}}=8.$ (8分)
$\because$点E为$\widehat{BC}$的中点,
$\therefore OE\perp BC,CP = BP=\frac{1}{2}BC = 4.$ (10分)
又$\because OA = OB,$
$\therefore OP$是$\triangle ABC$的中位线.
$\therefore OP=\frac{1}{2}AC = 3.$ (11分)
$\therefore PE = OE - OP = 5 - 3 = 2.$ (12分)
$\therefore CE=\sqrt{CP^{2}+PE^{2}}=\sqrt{4^{2}+2^{2}}=2\sqrt{5}.$ (13分)

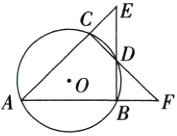
16. (本题15分)如图，AB，AC是⊙O的弦，点D是$\widehat{BC}$的中点，连接BD，CD并延长，分别交AC，AB的延长线于点E，F，且DE = DF.
(1)求证：AC = AB.
(2)若BD = 3，CE = 4，求AB的长.

答案：
(1)证明:$\because$点D是$\widehat{BC}$的中点,
$\therefore\widehat{CD}=\widehat{BD}.\therefore CD = BD.$ (2分)
在$\triangle CED$和$\triangle BFD$中,
$\because CD = BD,\angle CDE=\angle BDF,DE = DF,$
$\therefore\triangle CED\cong\triangle BFD.$ (3分)
$\therefore CE = BF,\angle E=\angle F.$ (4分)
$\because CD = BD,DE = DF,$
$\therefore BD + DE = CD + DF$,即$BE = CF.$ (5分)
在$\triangle BAE$和$\triangle CAF$中,
$\because\angle A=\angle A,\angle E=\angle F,BE = CF,$
$\therefore\triangle BAE\cong\triangle CAF.$ (6分)
$\therefore AE = AF.$ (7分)
$\therefore AE - CE = AF - BF$,即$AC = AB.$ (8分)
(2)解:$\because$四边形ABDC是$\odot O$的内接四边形,
$\therefore\angle ACD+\angle ABD = 180^{\circ}.$ (10分)
由
(1)知$\triangle BAE\cong\triangle CAF,$
$\therefore\angle ABD=\angle ACD.\therefore\angle ABD=\angle ACD = 90^{\circ}.$
$\therefore\angle ECD = 90^{\circ}.$ (11分)
$\because CD = BD = 3,CE = 4,$
$\therefore DE=\sqrt{CD^{2}+CE^{2}}=5.$ (12分)
$\therefore BE = DE + BD = 5 + 3 = 8.$ (13分)
设$AB = AC = x$,则$AE = x + 4.$
在$Rt\triangle ABE$中,$AB^{2}+BE^{2}=AE^{2},$
即$x^{2}+8^{2}=(x + 4)^{2}$,解得$x = 6.$
$\therefore AB = 6.$ (15分)