《2025年名校作业九年级数学下册北师大版》

10.在Rt△ABC中，∠C = 90°，tanA = $\frac{7}{24}$，则cosA的值为（ ）
A.$\frac{25}{24}$
B.$\frac{24}{7}$
C.$\frac{7}{25}$
D.$\frac{24}{25}$

答案： D 【解析】在Rt△ABC中，
∵∠C = 90°，
∴tanA = $\frac{BC}{AC}=\frac{7}{24}$。
∴设BC = 7x，则AC = 24x。
∴AB = $\sqrt{AC^{2}+BC^{2}} = 25x$。
∴cosA = $\frac{AC}{AB}=\frac{24x}{25x}=\frac{24}{25}$。

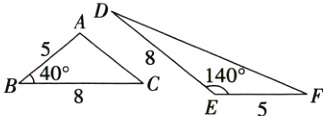
11.如图，在△ABC和△DEF中，AB = EF = 5，BC = DE = 8，∠ABC = 40°，∠DEF = 140°，则△ABC和△DEF的面积之比为（ ）

A.5:8
B.8:5
C.1:1
D.2:7

答案：
C 【解析】如图，过点A作AG⊥BC于点G，过点F作FH⊥DE交DE的延长线于点H，则∠AGB = ∠H = 90°，∠FEH = 180° - ∠DEF = 40°。

在Rt△ABG中，sinB = $\frac{AG}{AB}$，
∴AG = ABsinB = 5sin40°。
∴$S_{\triangle ABC}=\frac{1}{2}BC\cdot AG=\frac{1}{2}\times8\times5\sin40° = 20\sin40°$。在Rt△EFH中，sin∠FEH = $\frac{FH}{EF}$，
∴FH = EFsin∠FEH = 5sin40°。
∴$S_{\triangle DEF}=\frac{1}{2}DE\cdot FH=\frac{1}{2}\times8\times5\sin40° = 20\sin40°$。
∴$S_{\triangle ABC}:S_{\triangle DEF}=1:1$。

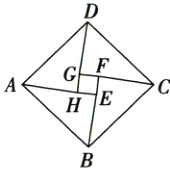
12.如图所示的“弦图”是由四个全等的直角三角形(△ABE，△BCF，△CDG，△DAH)和一个小正方形EFGH拼成的大正方形ABCD.若EF:AH = 1:3，则sin∠ABE的值为（ ）

A.$\frac{\sqrt{5}}{5}$
B.$\frac{3}{5}$
C.$\frac{4}{5}$
D.$\frac{2\sqrt{5}}{5}$

答案： C 【解析】
∵EF:AH = 1:3，
∴设EF = x，则AH = 3x。
∵△ABE≌△DAH，四边形EFGH为正方形，
∴BE = AH = 3x，HE = EF = x。
∴AE = AH+HE = 4x。在Rt△ABE中，根据勾股定理，得AB = $\sqrt{AE^{2}+BE^{2}} = 5x$。
∴sin∠ABE = $\frac{AE}{AB}=\frac{4x}{5x}=\frac{4}{5}$。

13.如图，在△ABC中，AB = 3，AC = 4，BC = 5，点P在AC上，且PB = PC.求sin∠ABP的值.

答案： 解：
∵AB = 3，AC = 4，BC = 5，
∴AB²+AC² = BC²。
∴△ABC是直角三角形，且∠A = 90°。设PA = x，则PC = AC - PA = 4 - x。
∵PB = PC，
∴PB = 4 - x。在Rt△ABP中，AB²+PA² = PB²，即3²+x² = (4 - x)²。解得x = $\frac{7}{8}$。
∴PA = $\frac{7}{8}$。
∴PB = 4 - $\frac{7}{8}=\frac{25}{8}$。
∴sin∠ABP = $\frac{PA}{PB}=\frac{\frac{7}{8}}{\frac{25}{8}}=\frac{7}{25}$。

14.如图，在菱形ABCD中，对角线AC，BD相交于点O.若AC = 6，BD = 2，求sin∠BAD的值.

答案：
解：如图，过点D作DE⊥AB于点E，则∠AED = 90°。

∵四边形ABCD是菱形，
∴AC⊥BD，AD = AB，OA = $\frac{1}{2}AC=\frac{1}{2}\times6 = 3$，OB = $\frac{1}{2}BD=\frac{1}{2}\times2 = 1$。在Rt△OAB中，由勾股定理，得AB = $\sqrt{OA^{2}+OB^{2}}=\sqrt{10}$。
∴AD = $\sqrt{10}$。
∵$S_{菱形ABCD}=AB\cdot DE=\frac{1}{2}AC\cdot BD$，
∴DE = $\frac{AC\cdot BD}{2AB}=\frac{6\times2}{2\sqrt{10}}=\frac{3\sqrt{10}}{5}$。在Rt△ADE中，sin∠BAD = $\frac{DE}{AD}=\frac{\frac{3\sqrt{10}}{5}}{\sqrt{10}}=\frac{3}{5}$。

15.【教材P7习题T5变式】在△ABC中，AB = 5，AC = 2$\sqrt{5}$，△ABC的面积为10，求BC的长和sinB的值.

答案：
解：分两种情况：
如图①，当∠BAC为钝角时，过点C作CD⊥AB，交BA的延长线于点D，则∠D = 90°。
∵$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD = 10$，AB = 5，
∴CD = 4。在Rt△ACD中，由勾股定理，得AD = $\sqrt{AC^{2}-CD^{2}}=\sqrt{(2\sqrt{5})^{2}-4^{2}} = 2$。
∴BD = AB+AD = 5 + 2 = 7。
∴BC = $\sqrt{BD^{2}+CD^{2}}=\sqrt{7^{2}+4^{2}}=\sqrt{65}$。
∴sinB = $\frac{CD}{BC}=\frac{4}{\sqrt{65}}=\frac{4\sqrt{65}}{65}$。
　
如图②，当∠BAC为锐角时，过点C作CD⊥AB于点D，则∠BDC = ∠ADC = 90°。
∵$S_{\triangle ABC}=\frac{1}{2}AB\cdot CD = 10$，AB = 5，
∴CD = 4。在Rt△ACD中，由勾股定理，得AD = $\sqrt{AC^{2}-CD^{2}}=\sqrt{(2\sqrt{5})^{2}-4^{2}} = 2$。
∴BD = AB - AD = 5 - 2 = 3。
∴BC = $\sqrt{BD^{2}+CD^{2}}=\sqrt{3^{2}+4^{2}} = 5$。
∴sinB = $\frac{CD}{BC}=\frac{4}{5}$。
综上，BC的值为$\sqrt{65}$或5，sinB的值为$\frac{4\sqrt{65}}{65}$或$\frac{4}{5}$。