2025年名校作业九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校作业九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 中国廊桥是桥梁与房屋的珠联璧合,代表着中国人的智慧,是世界文明宝库的一大奇观.如图是某座抛物线型廊桥,已知抛物线的表达式为$y = -\frac{1}{40}x^{2}+12$,为保护廊桥的安全,要在该抛物线上距水面AB高度为8米的点E,F处安装两盏警示灯,则这两盏灯的水平距离EF为 ( )
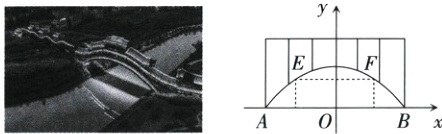
A. $8\sqrt{10}$米
B. 16米
C. $8\sqrt{5}$米
D. $16\sqrt{2}$米

A. $8\sqrt{10}$米
B. 16米
C. $8\sqrt{5}$米
D. $16\sqrt{2}$米
答案:
A
解析:当$y = 8$时,$-\frac{1}{40}x^{2}+12 = 8$,
解得$x_{1}=-4\sqrt{10},x_{2}=4\sqrt{10}$.
所以这两盏灯的水平距离$EF$为$4\sqrt{10}-(-4\sqrt{10}) = 8\sqrt{10}$(米).
解析:当$y = 8$时,$-\frac{1}{40}x^{2}+12 = 8$,
解得$x_{1}=-4\sqrt{10},x_{2}=4\sqrt{10}$.
所以这两盏灯的水平距离$EF$为$4\sqrt{10}-(-4\sqrt{10}) = 8\sqrt{10}$(米).
2. 某中学在科技实验活动中,设计制作了“水火箭”升空实验,已知“水火箭”的升空高度$h$(m)与飞行时间$t$(s)满足函数关系式$h = at^{2}+bt + 1$,且“水火箭”飞行3 s和飞行9 s时的升空高度相同,飞行8 s时的升空高度为33 m,则“水火箭”升空的最大高度为 ( )
A. 33 m
B. 36 m
C. 37 m
D. 40 m
A. 33 m
B. 36 m
C. 37 m
D. 40 m
答案:
C
解析:根据题意,得$\begin{cases}-\frac{b}{2a}=\frac{3 + 9}{2}\\64a + 8b + 1 = 33\end{cases}$,
解得$\begin{cases}a=-1\\b = 12\end{cases}$.
$\therefore h=-t^{2}+12t + 1=-(t - 6)^{2}+37$.
$\therefore$当$t = 6$时,$h_{最大}=37$.
因此,“水火箭”升空的最大高度为37米.
解析:根据题意,得$\begin{cases}-\frac{b}{2a}=\frac{3 + 9}{2}\\64a + 8b + 1 = 33\end{cases}$,
解得$\begin{cases}a=-1\\b = 12\end{cases}$.
$\therefore h=-t^{2}+12t + 1=-(t - 6)^{2}+37$.
$\therefore$当$t = 6$时,$h_{最大}=37$.
因此,“水火箭”升空的最大高度为37米.
3. 物理实验课上,小明绘制的电路图如图①所示,将变阻器R的滑片从一端滑到另一端,变阻器R消耗的电功率P随电流I变化的关系图象如图②所示,已知该图象是经过原点的一条抛物线的一部分,则变阻器R消耗的最大电功率为 ( )
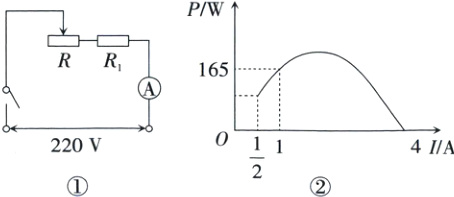
A. 160 W
B. 180 W
C. 200 W
D. 220 W

A. 160 W
B. 180 W
C. 200 W
D. 220 W
答案:
D
解析:设抛物线的表达式为$P = aI^{2}+bI$.
把$(1,165),(4,0)$代入,得$\begin{cases}a + b = 165\\16a + 4b = 0\end{cases}$.
解得$\begin{cases}a=-55\\b = 220\end{cases}$.
$\therefore$抛物线的表达式为$P=-55I^{2}+220I=-55(I - 2)^{2}+220$.
$\therefore$当$I = 2$时,$P_{最大}=220$.
因此,变阻器$R$消耗的最大电功率为220 W.
解析:设抛物线的表达式为$P = aI^{2}+bI$.
把$(1,165),(4,0)$代入,得$\begin{cases}a + b = 165\\16a + 4b = 0\end{cases}$.
解得$\begin{cases}a=-55\\b = 220\end{cases}$.
$\therefore$抛物线的表达式为$P=-55I^{2}+220I=-55(I - 2)^{2}+220$.
$\therefore$当$I = 2$时,$P_{最大}=220$.
因此,变阻器$R$消耗的最大电功率为220 W.
4. 如图是一座抛物线型拱桥,当桥下水面宽度是4 m时,拱顶到水面的距离是2 m,则水面下降1 m后,水面的宽度是 ( )
A. 6 m B. $\sqrt{6}$ m
C. $2\sqrt{6}$ m D. $3\sqrt{6}$ m
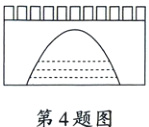
A. 6 m B. $\sqrt{6}$ m
C. $2\sqrt{6}$ m D. $3\sqrt{6}$ m

答案:
C
解析:如图,以水面宽度是4 m时,水面所在的直线为$x$轴,以这座抛物线型拱桥的对称轴为$y$轴,建立平面直角坐标系.

设抛物线的表达式是$y = ax^{2}+b$.
$\because$当桥下水面宽度是4 m时,拱顶到水面的距离是2 m,
$\therefore$抛物线经过点$(2,0),(0,2)$.
将$(2,0),(0,2)$代入$y = ax^{2}+b$,
得$\begin{cases}4a + b = 0\\b = 2\end{cases}$,解得$\begin{cases}a=-\frac{1}{2}\\b = 2\end{cases}$.
$\therefore$抛物线的表达式是$y=-\frac{1}{2}x^{2}+2$.
令$y=-1$,即$-\frac{1}{2}x^{2}+2=-1$,解得$x_{1}=\sqrt{6},x_{2}=-\sqrt{6}$.
$\sqrt{6}-(-\sqrt{6})=2\sqrt{6}(m)$.
$\therefore$水面下降1 m后,水面的宽度是$2\sqrt{6}$m.
C
解析:如图,以水面宽度是4 m时,水面所在的直线为$x$轴,以这座抛物线型拱桥的对称轴为$y$轴,建立平面直角坐标系.

设抛物线的表达式是$y = ax^{2}+b$.
$\because$当桥下水面宽度是4 m时,拱顶到水面的距离是2 m,
$\therefore$抛物线经过点$(2,0),(0,2)$.
将$(2,0),(0,2)$代入$y = ax^{2}+b$,
得$\begin{cases}4a + b = 0\\b = 2\end{cases}$,解得$\begin{cases}a=-\frac{1}{2}\\b = 2\end{cases}$.
$\therefore$抛物线的表达式是$y=-\frac{1}{2}x^{2}+2$.
令$y=-1$,即$-\frac{1}{2}x^{2}+2=-1$,解得$x_{1}=\sqrt{6},x_{2}=-\sqrt{6}$.
$\sqrt{6}-(-\sqrt{6})=2\sqrt{6}(m)$.
$\therefore$水面下降1 m后,水面的宽度是$2\sqrt{6}$m.
5. 如图,某农场计划修建三间矩形饲养室,饲养室一面靠现有墙,可用墙长为20 m,中间用两道墙隔开,已知计划中的修筑材料可建围墙总长为60 m,则饲养室的占地总面积有 ( )
A. 最小值$200m^{2}$ B. 最小值$225m^{2}$
C. 最大值$200m^{2}$ D. 最大值$225m^{2}$
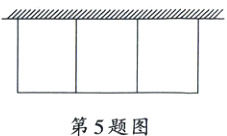
A. 最小值$200m^{2}$ B. 最小值$225m^{2}$
C. 最大值$200m^{2}$ D. 最大值$225m^{2}$

答案:
C
解析:设饲养室垂直于墙的一边的长为$x$m,占地总面积为$y$m²,则另一边的长为$(60 - 4x)$m.
根据题意,得$0\lt x\lt\frac{60}{4},0\lt60 - 4x\leqslant20$,
解得$10\leqslant x\lt15$.
$y=x(60 - 4x)=-4x^{2}+60x=-4(x - 7.5)^{2}+225$.
$\therefore$当$x\gt7.5$时,$y$随$x$的增大而减小.
$\therefore$当$x = 10$时,$y$取得最大值,为$-4\times(10 - 7.5)^{2}+225 = 200$.
因此,饲养室的占地总面积有最大值200 m².
解析:设饲养室垂直于墙的一边的长为$x$m,占地总面积为$y$m²,则另一边的长为$(60 - 4x)$m.
根据题意,得$0\lt x\lt\frac{60}{4},0\lt60 - 4x\leqslant20$,
解得$10\leqslant x\lt15$.
$y=x(60 - 4x)=-4x^{2}+60x=-4(x - 7.5)^{2}+225$.
$\therefore$当$x\gt7.5$时,$y$随$x$的增大而减小.
$\therefore$当$x = 10$时,$y$取得最大值,为$-4\times(10 - 7.5)^{2}+225 = 200$.
因此,饲养室的占地总面积有最大值200 m².
6. 某商品的进价为28元,当每件的售价为50元时,每天能售出32件,每件的售价每降低1元,每天可多售出2件.店主要想使每天的利润最大,应将每件的售价降低________元.
答案:
3
解析:设该商品每件的售价降低$x$元,每天的利润为$w$元.
根据题意,得$w=(50 - 28 - x)(32 + 2x)=-2x^{2}+12x + 704=-2(x - 3)^{2}+722$.
$\therefore$当$x = 3$时,$w_{最大}=722$.
因此,店主要想使每天的利润最大,应将每件的售价降低3元.
解析:设该商品每件的售价降低$x$元,每天的利润为$w$元.
根据题意,得$w=(50 - 28 - x)(32 + 2x)=-2x^{2}+12x + 704=-2(x - 3)^{2}+722$.
$\therefore$当$x = 3$时,$w_{最大}=722$.
因此,店主要想使每天的利润最大,应将每件的售价降低3元.
7. 如图是一款抛物线型落地灯筒示意图,防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.5米,灯柱$AB = 1.5$米,最高点C到灯柱的距离为1.6米.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为________米.
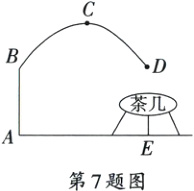

答案:
3.2
解析:根据题意,得点$B$与点$D$关于抛物线的对称轴对称.
$\therefore AE = 2\times1.6 = 3.2$(米).
解析:根据题意,得点$B$与点$D$关于抛物线的对称轴对称.
$\therefore AE = 2\times1.6 = 3.2$(米).
8. 某广场有一个直径为16米的圆形喷水池,喷水池的外边沿有一圈喷水头(喷水头高度忽略不计).如图,各方向喷出的水柱恰好在喷水池中心O的上方A处汇合,水柱离OA的距离为3米时水柱到达最高点,此时水柱离地面5米.王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的他站立时到OA的距离需在________米以内.
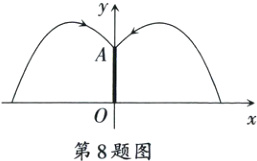

答案:
7
解析:设$OA$右侧抛物线的表达式为$y = a(x - 3)^{2}+5$.
由题意,可得该抛物线过点$(8,0)$,
$\therefore 25a+5 = 0$,解得$a=-\frac{1}{5}$.
$\therefore OA$右侧抛物线的表达式为$y=-\frac{1}{5}(x - 3)^{2}+5$.
当$y = 1.8$时,$-\frac{1}{5}(x - 3)^{2}+5 = 1.8$,
解得$x_{1}=7,x_{2}=-1$(舍去).
因此,为了不被淋湿,身高1.8米的王师傅站立时到$OA$的距离需在7米以内.
解析:设$OA$右侧抛物线的表达式为$y = a(x - 3)^{2}+5$.
由题意,可得该抛物线过点$(8,0)$,
$\therefore 25a+5 = 0$,解得$a=-\frac{1}{5}$.
$\therefore OA$右侧抛物线的表达式为$y=-\frac{1}{5}(x - 3)^{2}+5$.
当$y = 1.8$时,$-\frac{1}{5}(x - 3)^{2}+5 = 1.8$,
解得$x_{1}=7,x_{2}=-1$(舍去).
因此,为了不被淋湿,身高1.8米的王师傅站立时到$OA$的距离需在7米以内.
查看更多完整答案,请扫码查看


