《2025年名校作业九年级数学下册北师大版》

10. 如图为一节楼梯的示意图,BC⊥AC,∠BAC = α,AC = 6米.现要在楼梯上铺一块地毯,楼梯宽度为1米,则地毯的面积至少为_______平方米.

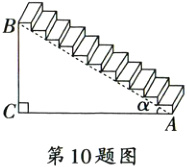
答案： (6 + 6tanα)

11. 如图,在Rt△ABC中,∠ACB = 90°,CD⊥AB于点D.已知BC = 3,AC = 4,则cos∠BCD = ________.

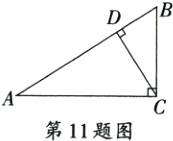
答案： $\frac{4}{5}$

12. 在△ABC中,AB = AC = 5,△ABC的面积为10,则sinB的值为________.

答案： $\frac{2\sqrt{5}}{5}$或$\frac{\sqrt{5}}{5}$

13. (本大题共2个小题,每小题6分,共12分)
计算:
(1) 2cos30° + 4sin30° - tan60°;
(2) 2sin²45° - 6cos30° + 3tan45° + 4sin60°.

答案： 解：
(1)2cos30° + 4sin30° - tan60°
= 2×$\frac{\sqrt{3}}{2}$ + 4×$\frac{1}{2}$ - $\sqrt{3}$ (3分)
= $\sqrt{3}$ + 2 - $\sqrt{3}$
= 2. (6分)
(2)2sin²45° - 6cos30° + 3tan45° + 4sin60°
= 2×($\frac{\sqrt{2}}{2}$)² - 6×$\frac{\sqrt{3}}{2}$ + 3×1 + 4×$\frac{\sqrt{3}}{2}$ (4分)
= 2×$\frac{2}{4}$ - 3$\sqrt{3}$ + 3 + 2$\sqrt{3}$
= 4 - $\sqrt{3}$. (6分)

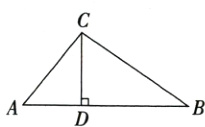
14. (本题11分) 如图,在△ABC中,CD⊥AB,垂足为点D.若AB = 12,CD = 6,tanA = $\frac{3}{2}$.
(1) 求BD的长;
(2) 求sinB的值.

答案： 解：
(1)
∵CD⊥AB，
∴∠ADC = ∠BDC = 90°. (1分)
在Rt△ACD中，AD = $\frac{CD}{tanA}$ = $\frac{6}{\frac{3}{2}}$ = 4. (5分)
∴BD = AB - AD = 12 - 4 = 8. (6分)
(2)在Rt△BCD中，由勾股定理，得BC = $\sqrt{BD^{2}+CD^{2}}$ = 10. (8分)
∴sinB = $\frac{CD}{BC}$ = $\frac{3}{5}$. (11分)

15. (本题11分) 如图①是某城市广场地下停车场的入口,图②是安装雨棚左侧支架的示意图,已知支架的立柱BC与地面垂直(∠BCA = 90°),BC = 1.5 m,点F,A,C在同一水平线上,斜杆AB与水平线AC的夹角∠BAC = 30°,AD = 1 m,支撑杆DE⊥AB于点D,支架的边BE与AB的夹角∠EBD = 60°.求支架的边BE的长.

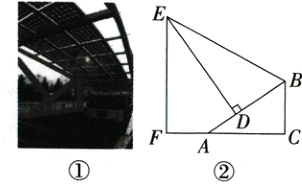
答案： 解：在Rt△ABC中，AB = $\frac{BC}{sin\angle BAC}$ = $\frac{1.5}{sin30°}$ = 3(m). (4分)
∴BD = AB - AD = 3 - 1 = 2(m). (5分)
∵DE⊥AB，
∴∠BDE = 90°. (6分)
在Rt△BDE中，BE = $\frac{BD}{cos\angle EBD}$ = $\frac{2}{cos60°}$ = 4(m). (10分)
∴支架的边BE的长为4 m. (11分)

16. (本题14分) 阅读下列材料,并解答问题.
若将一个角扩大为原来的2倍,则这个角的正弦值将如何变化?
如图,在Rt△ABC中,∠ACB = 90°,AB = 2,∠A = α,OC是AB边上的中线,CD⊥AB于点D,则OC = $\frac{1}{2}$AB = 1,∠COD = 2α,于是sin2α = $\frac{CD}{OC}$ = $\frac{AC\cdot\sin\alpha}{1}$ = AB·cosα·sinα = 2sinα·cosα.
(1) 若BC = 1,则sinα的值为________,sin2α的值为________;
(2) 请你参考以上推导思路,求tan2α的表达式.(用含sinα,cosα的式子表示)

答案： 解：
(1)$\frac{1}{2}$ (2分)
$\frac{\sqrt{3}}{2}$ (4分)
(2)答案1：
∵OC是AB边上的中线，
∴OA = $\frac{1}{2}$AB = 1. (5分)
∴tan2α = $\frac{CD}{OD}$
= $\frac{AC·sin\alpha}{AD - OA}$
= $\frac{AB·cos\alpha·sin\alpha}{AC·cos\alpha - 1}$
= $\frac{2sin\alpha·cos\alpha}{AB·cos\alpha·cos\alpha - 1}$
= $\frac{2sin\alpha·cos\alpha}{2(cos\alpha)^{2}-1}$. (14分)
答案2：
∵CD⊥AB，
∴∠BDC = 90°.
∴∠B + ∠BCD = 90°.
∵∠ACB = 90°，
∴∠A + ∠B = 90°.
∴∠BCD = ∠A = α. (5分)
∵OC是AB边上的中线，
∴OB = $\frac{1}{2}$AB = 1. (6分)
∴tan2α = $\frac{CD}{OD}$
= $\frac{AC·sin\alpha}{OB - BD}$
= $\frac{AB·cos\alpha·sin\alpha}{1 - BC·sin\alpha}$
= $\frac{2sin\alpha·cos\alpha}{1 - AB·sin\alpha·sin\alpha}$
= $\frac{2sin\alpha·cos\alpha}{1 - 2(sin\alpha)^{2}}$. (14分)