2025年名校作业九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校作业九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第19页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
9. 如图,线段AB表示一信号塔,DE表示一斜坡,DC⊥BC,CD = 36m,点A,B,C,D,E在同一平面内. 某人站在D处测得塔顶A处的仰角为37°,站在C处测得塔顶A处的仰角为48°(人的身高忽略不计).求信号塔AB的高度.(结果精确到1m;参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin48°≈0.74,cos48°≈0.67,tan48°≈1.1)
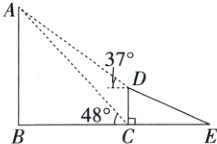

答案:
解:如图,过点D作DF⊥AB于点F,则∠AFD = 90°,BF = CD = 36 m,DF = BC。
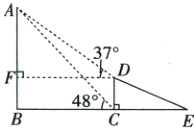
设AB = x m,则AF = AB - BF = (x - 36)m。
根据题意,得∠B = 90°,∠ADF = 37°,∠ACB = 48°。
在Rt△ABC中,BC = $\frac{AB}{tan\angle ACB}=\frac{x}{tan48°}$。
在Rt△ADF中,DF = $\frac{AF}{tan\angle ADF}=\frac{x - 36}{tan37°}$。
∴$\frac{x}{tan48°}=\frac{x - 36}{tan37°}$,解得x≈113。
因此,信号塔AB的高度约为113 m。
解:如图,过点D作DF⊥AB于点F,则∠AFD = 90°,BF = CD = 36 m,DF = BC。

设AB = x m,则AF = AB - BF = (x - 36)m。
根据题意,得∠B = 90°,∠ADF = 37°,∠ACB = 48°。
在Rt△ABC中,BC = $\frac{AB}{tan\angle ACB}=\frac{x}{tan48°}$。
在Rt△ADF中,DF = $\frac{AF}{tan\angle ADF}=\frac{x - 36}{tan37°}$。
∴$\frac{x}{tan48°}=\frac{x - 36}{tan37°}$,解得x≈113。
因此,信号塔AB的高度约为113 m。
10. 为增强民众生活幸福感,某社区服务队在休闲活动场所的墙上安装了如图①所示的遮阳棚,方便居民使用. 如图②是其侧面示意图,遮阳棚BC长4m,与水平线的夹角为30°,且靠墙端离地的高AB为5m,当太阳光线CD与地面AD的夹角为67°时,求AD的长.(结果精确到0.1m;参考数据:$\sqrt{3}$≈1.73,sin67°≈$\frac{12}{13}$,cos67°≈$\frac{5}{13}$,tan67°≈$\frac{12}{5}$)
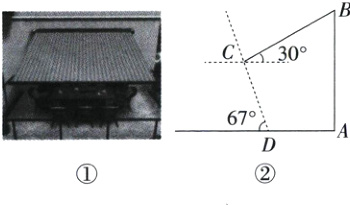

答案:
解:如图,过点C分别作CE⊥AB于点E,CF⊥AD交AD的延长线于点F,则∠CEB = ∠CFD = 90°,CF = AE,AF = CE。

在Rt△BCE中,BE = $\frac{1}{2}BC = 2$m,CE = BCcos∠BCE = 4cos30°≈3.46(m)。
∴AE = AB - BE = 5 - 2 = 3(m),AF≈3.46 m。
∴CF = 3 m。
在Rt△CDF中,DF = $\frac{CF}{tan\angle CDF}=\frac{3}{tan67°}\approx1.25$(m)。
∴AD = AF - DF≈2.2 m。
∴AD的长约为2.2 m。
解:如图,过点C分别作CE⊥AB于点E,CF⊥AD交AD的延长线于点F,则∠CEB = ∠CFD = 90°,CF = AE,AF = CE。

在Rt△BCE中,BE = $\frac{1}{2}BC = 2$m,CE = BCcos∠BCE = 4cos30°≈3.46(m)。
∴AE = AB - BE = 5 - 2 = 3(m),AF≈3.46 m。
∴CF = 3 m。
在Rt△CDF中,DF = $\frac{CF}{tan\angle CDF}=\frac{3}{tan67°}\approx1.25$(m)。
∴AD = AF - DF≈2.2 m。
∴AD的长约为2.2 m。
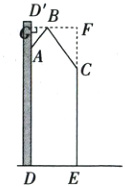
11. 图①是一种淋浴喷头,图②是其简化示意图,用支架把喷头固定在点A处,手柄长AB = 25cm,AB与墙壁DD'的夹角∠D'AB = 37°,喷出的水流BC与AB形成的夹角∠ABC = 72°.现在住户要求:当人站在与墙壁DD'距离为50cm的E处淋浴时,水流正好喷洒在人体的C处,CE = 130cm. 问:安装师傅应将喷头固定在离地面多高的位置?(结果精确到1cm;参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
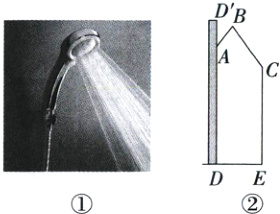

答案:
解:如图,过点B作BG⊥D'D于点G,延长EC,GB交于点F,则四边形DEFG是矩形,∠AGB = ∠F = 90°。
∴FG = DE = 50 cm,DG = EF。
∵∠BAG = 37°,
∴∠ABG = 90° - ∠BAG = 53°,AG = ABcos∠BAG = 25cos37°≈20(cm),BG = ABsin∠BAG = 25sin37°≈15(cm)。
∴BF = FG - BG≈50 - 15 = 35(cm)。
∵∠ABC = 72°,
∴∠CBF = 180° - ∠ABG - ∠ABC = 55°。
∴CF = BFtan∠CBF≈35tan55°≈50.1(cm)。
∴EF = CF + CE≈50.1 + 130 = 180.1(cm)。
∴DG≈180.1 cm。
∴AD = DG - AG≈180.1 - 20≈160(cm)。
因此安装师傅应将喷头固定在离地面约160 cm的位置。
解:如图,过点B作BG⊥D'D于点G,延长EC,GB交于点F,则四边形DEFG是矩形,∠AGB = ∠F = 90°。

∴FG = DE = 50 cm,DG = EF。
∵∠BAG = 37°,
∴∠ABG = 90° - ∠BAG = 53°,AG = ABcos∠BAG = 25cos37°≈20(cm),BG = ABsin∠BAG = 25sin37°≈15(cm)。
∴BF = FG - BG≈50 - 15 = 35(cm)。
∵∠ABC = 72°,
∴∠CBF = 180° - ∠ABG - ∠ABC = 55°。
∴CF = BFtan∠CBF≈35tan55°≈50.1(cm)。
∴EF = CF + CE≈50.1 + 130 = 180.1(cm)。
∴DG≈180.1 cm。
∴AD = DG - AG≈180.1 - 20≈160(cm)。
因此安装师傅应将喷头固定在离地面约160 cm的位置。
查看更多完整答案,请扫码查看


