《2025年名校作业九年级数学下册北师大版》

1. 如图,某购物广场要修建一个地下停车场,其斜坡AD的坡角为25°,层高CD为3m. 求该停车场入口可通过汽车的最大高度.(结果精确到0.1m;参考数据:sin25°≈0.42,cos25°≈0.91,tan25°≈0.47)
　　　　　　　　

答案：
解：如图，过点C作CE⊥AD于点E，则∠CED = 90°。

∴∠DCE + ∠CDE = 90°。
由题意，得∠CDB = 90°，∠ADB = 25°。
∴∠CDE + ∠ADB = 90°。
∴∠DCE = ∠ADB = 25°。
在Rt△CDE中，CE = CDcos∠DCE = 3cos25°≈2.7(m)。
因此，该停车场入口可通过汽车的最大高度约为2.7 m。

2. 如图是某小区入口的平面示意图,已知入口BC宽4米,栏杆支点O与地面BC的距离为0.8米,当栏杆OM升起到与门卫室外墙AB的夹角为30°时,一辆宽2.4米,高1.6米的轿车能否从该入口的正中间位置进入? 试说明理由.(参考数据:$\sqrt{3}$≈1.73)
　　　　　　　　　　

答案：
解：能。
理由：当轿车从该入口的正中间位置进入时，车与AB的距离为(4 - 2.4)÷2 = 0.8(米)。
如图，在BC上取点Q，使BQ = 0.8米，过点Q作QP⊥BC交OM于点P，过O作ON⊥PQ于点N，则四边形ONQB是矩形。

∴NQ = OB = 0.8米，ON = BQ = 0.8米。
由题意，得∠AOM = 30°。
∴∠PON = 90° - ∠AOM = 60°。
∴PN = ONtan∠PON = 0.8tan60°≈1.38(米)。
∴PQ = PN + NQ = 1.38 + 0.8 = 2.18(米)。
∵2.18 ＞ 1.6，
∴轿车能从该入口的正中间位置进入。

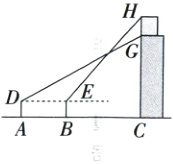
3. 如图,某数学小组要测量信号发射塔GH的高度,在与楼CG距离为60米的A处用测角仪测得发射塔底部G的仰角为30°,前进20米后在B处测得发射塔顶部H的仰角为50°.已知点A,B,C在同一直线上,请根据测量数据,求信号发射塔GH的高度.(参考数据:$\sqrt{3}$≈1.73,sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
　　　　　　　　　　　　　　　　　　　

答案：
解：如图，延长DE交CG于点F，则∠DFH = 90°，由题意，知DF = AC = 60米，EF = BC = AC - AB = 40米，∠FDG = 30°，∠FEH = 50°。

在Rt△DFG中，FG = DFtan∠FDG = 60tan30°≈34.6(米)。
在Rt△EFH中，FH = EFtan∠FEH = 40tan50°≈47.6(米)。
∴GH = FH - FG = 47.6 - 34.6 = 13(米)。
因此，信号发射塔GH的高度约为13米。

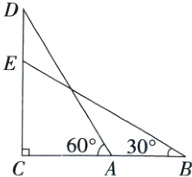
4. 如图,某数学兴趣小组要测量建筑物CD的高度,在A处测得建筑物顶部点D的仰角为60°,在B处测得建筑物上点E的仰角为30°,已知点C,A,B在同一直线上,AB=14米,DE=3米,求建筑物CD的高度.(结果保留根号)
　　　　　　　　　　　　　　　　　　

答案： 解：设CD = x米，则CE = CD - DE = (x - 3)米。
∵∠CAD = 60°，
∴AC = $\frac{CD}{tan\angle CAD}=\frac{\sqrt{3}}{3}x$。
∵∠CBE = 30°，
∴BC = $\frac{CE}{tan\angle CBE}=\sqrt{3}(x - 3)$。
∵BC - AC = AB，
∴$\sqrt{3}(x - 3)-\frac{\sqrt{3}}{3}x = 14$，解得$x = 7\sqrt{3}+\frac{9}{2}$。
因此，建筑物CD的高度约为$(7\sqrt{3}+\frac{9}{2})$米。