2025年名校作业九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校作业九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第13页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
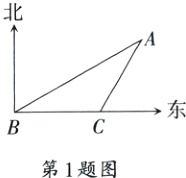
1. 如图,一艘轮船由西向东航行,在点B处测得小岛A在北偏东60°方向上,航行12 n mile到达点C处时,测得小岛A在北偏东30°方向上,则小岛A到航线BC的距离是______n mile.(结果保留根号)

答案:
$6\sqrt{3}$ 解析 如图,过点A作AE⊥BC,交BC的延长线于点E,则∠AEB = 90°。

由题意,得∠BAE = 60°,∠CAE = 30°。
∴∠ABC = 90° - ∠BAE = 30°,∠BAC = ∠BAE - ∠CAE = 30°。
∴∠ABC = ∠BAC。
∴AC = BC = 12 n mile。
在Rt△ACE中,AE = ACcos∠CAE = 12cos30° = $6\sqrt{3}$(n mile)。
∴小岛A到航线BC的距离是$6\sqrt{3}$ n mile。
$6\sqrt{3}$ 解析 如图,过点A作AE⊥BC,交BC的延长线于点E,则∠AEB = 90°。

由题意,得∠BAE = 60°,∠CAE = 30°。
∴∠ABC = 90° - ∠BAE = 30°,∠BAC = ∠BAE - ∠CAE = 30°。
∴∠ABC = ∠BAC。
∴AC = BC = 12 n mile。
在Rt△ACE中,AE = ACcos∠CAE = 12cos30° = $6\sqrt{3}$(n mile)。
∴小岛A到航线BC的距离是$6\sqrt{3}$ n mile。
2. 如图,一艘海轮位于灯塔P的东南方向上,距离灯塔100 n mile的A处,它沿正南方向以50$\sqrt{2}$ n mile/h的速度航行______h后,到达位于灯塔P南偏东30°方向上的B处.


答案:
$(\sqrt{3}-1)$ 解析 如图,延长BA交PQ于点C,则∠PCB = 90°。

根据题意,得∠PAC = 45°,∠B = 30°,PA = 100 n mile。
在Rt△PAC中,PC = PAsin∠PAC = 100sin45° = $50\sqrt{2}$(n mile),AC = PAcos∠PAC = 100cos45° = $50\sqrt{2}$(n mile)。
在Rt△PBC中,BC = $\frac{PC}{\tan B}$ = $\frac{50\sqrt{2}}{\tan 30°}$ = $50\sqrt{6}$(n mile)。
∴AB = BC - AC = $(50\sqrt{6}-50\sqrt{2})$ n mile。
$(50\sqrt{6}-50\sqrt{2})\div50\sqrt{2}=(\sqrt{3}-1)$ h。
∴它沿正南方向以$50\sqrt{2}$ n mile/h的速度航行$(\sqrt{3}-1)$ h后,到达位于灯塔P南偏东30°方向上的B处。
$(\sqrt{3}-1)$ 解析 如图,延长BA交PQ于点C,则∠PCB = 90°。

根据题意,得∠PAC = 45°,∠B = 30°,PA = 100 n mile。
在Rt△PAC中,PC = PAsin∠PAC = 100sin45° = $50\sqrt{2}$(n mile),AC = PAcos∠PAC = 100cos45° = $50\sqrt{2}$(n mile)。
在Rt△PBC中,BC = $\frac{PC}{\tan B}$ = $\frac{50\sqrt{2}}{\tan 30°}$ = $50\sqrt{6}$(n mile)。
∴AB = BC - AC = $(50\sqrt{6}-50\sqrt{2})$ n mile。
$(50\sqrt{6}-50\sqrt{2})\div50\sqrt{2}=(\sqrt{3}-1)$ h。
∴它沿正南方向以$50\sqrt{2}$ n mile/h的速度航行$(\sqrt{3}-1)$ h后,到达位于灯塔P南偏东30°方向上的B处。
3. 为了丰富学生的文化生活,某校组织学生分别到素质教育基地A和科技智能馆B参观学习. 已知A,B两地分别位于学校C的北偏西10°和北偏西47°方向上,B在A的南偏西37°方向上,且A,B两地相距900米,则去A地的学生比去B地的学生多走多少米?(参考数据:sin37°≈0.6,cos37°≈0.8,tan37°≈0.75,sin47°≈0.73,cos47°≈0.68,tan47°≈1.07)


答案:
解:如图,过点B作BE⊥AC于点E,则∠AEB = ∠CEB = 90°。
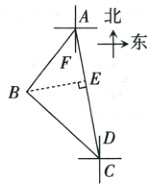
根据题意,得∠ACD = 10°,∠BCD = 47°,∠FAB = 37°,AB = 900米,CD//FA。
∴∠CAF = ∠ACD = 10°,∠BCE = ∠BCD - ∠ACD = 37°。
∴∠BAE = ∠FAB + ∠CAF = 47°。
在Rt△ABE中,AE = ABcos∠BAE = 900cos47°≈612(米),BE = ABsin∠BAE = 900sin47°≈657(米)。
在Rt△BCE中,BC = $\frac{BE}{\sin\angle BCE}$ = $\frac{657}{\sin 37°}$≈1 095(米),CE = $\frac{BE}{\tan\angle BCE}$ = $\frac{657}{\tan 37°}$≈876(米)。
∴AC = AE + CE≈1 488米。
∴AC - BC≈393米,即去A地的学生比去B地的学生多走393米。
解:如图,过点B作BE⊥AC于点E,则∠AEB = ∠CEB = 90°。

根据题意,得∠ACD = 10°,∠BCD = 47°,∠FAB = 37°,AB = 900米,CD//FA。
∴∠CAF = ∠ACD = 10°,∠BCE = ∠BCD - ∠ACD = 37°。
∴∠BAE = ∠FAB + ∠CAF = 47°。
在Rt△ABE中,AE = ABcos∠BAE = 900cos47°≈612(米),BE = ABsin∠BAE = 900sin47°≈657(米)。
在Rt△BCE中,BC = $\frac{BE}{\sin\angle BCE}$ = $\frac{657}{\sin 37°}$≈1 095(米),CE = $\frac{BE}{\tan\angle BCE}$ = $\frac{657}{\tan 37°}$≈876(米)。
∴AC = AE + CE≈1 488米。
∴AC - BC≈393米,即去A地的学生比去B地的学生多走393米。
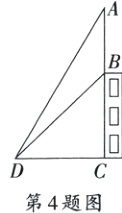
4. 如图,建筑物BC上有一旗杆AB,从距BC 40 m的D处观测旗杆顶部A的仰角为60°,观测旗杆底部B的仰角为45°,则旗杆AB的高度为________m.(结果保留根号)

答案:
$(40\sqrt{3}-40)$ 解析 根据题意,得CD = 40 m,∠ADC = 60°,∠BDC = 45°。
在Rt△ACD中,AC = CDtan∠ADC = $40\sqrt{3}$ m。
在Rt△BCD中,BC = CDtan∠BDC = 40 m。
∴AB = AC - BC = $(40\sqrt{3}-40)$ m,即旗杆AB的高度为$(40\sqrt{3}-40)$ m。
在Rt△ACD中,AC = CDtan∠ADC = $40\sqrt{3}$ m。
在Rt△BCD中,BC = CDtan∠BDC = 40 m。
∴AB = AC - BC = $(40\sqrt{3}-40)$ m,即旗杆AB的高度为$(40\sqrt{3}-40)$ m。
5. 如图,炎帝塑像DE在高55 m的小山EC上,在A处测得塑像底部E的仰角为34°,沿AC方向前进21 m到达B处,测得塑像顶部D的仰角为60°,则炎帝塑像DE的高度约为______m.(结果精确到1 m;参考数据:sin34°≈0.56,cos34°≈0.83,tan34°≈0.67,$\sqrt{3}$≈1.73)


答案:
51 解析 根据题意,得∠CAE = 34°,∠CBD = 60°,EC = 55 m,AB = 21 m。
在Rt△ACE中,AC = $\frac{EC}{\tan\angle CAE}$ = $\frac{55}{\tan 34°}$≈82.1。
∴BC = AC - AB≈82.1 - 21 = 61.1。
在Rt△BCD中,CD = BCtan∠CBD = 61.1tan60°≈105.7。
∴DE = CD - EC≈105.7 - 55≈51(m)。
∴炎帝塑像DE的高度约为51 m。
在Rt△ACE中,AC = $\frac{EC}{\tan\angle CAE}$ = $\frac{55}{\tan 34°}$≈82.1。
∴BC = AC - AB≈82.1 - 21 = 61.1。
在Rt△BCD中,CD = BCtan∠CBD = 61.1tan60°≈105.7。
∴DE = CD - EC≈105.7 - 55≈51(m)。
∴炎帝塑像DE的高度约为51 m。
6. 如图,在路边有相距10 m且高度相同的两盏路灯PQ,MN(灯杆垂直于地面). 小明在地面A处测得路灯PQ顶端的仰角为14°,向前行走25 m到达B处,测得路灯MN顶端的仰角为24.3°. 已知点A,B,Q,N在同一条直线上,请你利用所学知识帮助小明求出路灯的高度.(结果精确到0.1 m;参考数据:sin14°≈0.24,cos14°≈0.97,tan14°≈0.25,sin24.3°≈0.41,cos24.3°≈0.91,tan24.3°≈0.45)


答案:
解:由题意,得∠A = 14°,∠MBN = 24.3°,AB = 25 m,QN = 10 m。
设PQ = MN = x m。
在Rt△APQ中,AQ = $\frac{PQ}{\tan A}$ = $\frac{x}{\tan 14°}$。
在Rt△BMN中,BN = $\frac{MN}{\tan\angle MBN}$ = $\frac{x}{\tan 24.3°}$。
∵AQ + QN = AB + BN,
∴$\frac{x}{\tan 14°}$ + 10 = 25 + $\frac{x}{\tan 24.3°}$,解得x≈8.4。
所以,路灯的高度约为8.4 m。
设PQ = MN = x m。
在Rt△APQ中,AQ = $\frac{PQ}{\tan A}$ = $\frac{x}{\tan 14°}$。
在Rt△BMN中,BN = $\frac{MN}{\tan\angle MBN}$ = $\frac{x}{\tan 24.3°}$。
∵AQ + QN = AB + BN,
∴$\frac{x}{\tan 14°}$ + 10 = 25 + $\frac{x}{\tan 24.3°}$,解得x≈8.4。
所以,路灯的高度约为8.4 m。
查看更多完整答案,请扫码查看


