《2025年名校作业九年级数学下册北师大版》

7. 如图，我市在建高铁某段路基的横断面为梯形ABCD，DC//AB，坡面BC长6米，坡度为1:1，坡面AD的坡角为30°，则AD的长为________米.（结果保留根号）
　　　　　

答案：
$6\sqrt{2}$ 解析 如图，过点D作DE⊥AB于点E，过点C作CF⊥AB于点F，则∠AED = ∠CFB = 90°，DE = CF。
　　　　　
由题意，知∠A = 30°，CF:BF = 1:1。
∴BF = CF。
∴∠B = 45°。
在Rt△BCF中，CF = BCsinB = 6sin45° = $3\sqrt{2}$(米)。
∴DE = $3\sqrt{2}$米。
在Rt△ADE中，AD = $\frac{DE}{\sin A}$ = $\frac{3\sqrt{2}}{\sin 30°}$ = $6\sqrt{2}$(米)。

8. 某市政府根据各段隧道空间情况，在不影响交通的情况下，加装了如图所示的逃生爬梯. 起初工程师计划修建一段坡角为50°的爬梯AB，从安全角度再次考虑，最终修建了AD，EF两段坡角均为45°的平行爬梯，并在中间修建了1 m的水平平台DE. 已知C，B，F三点共线，AC=4 m，求修改后爬梯底部F与修改前爬梯底部B之间的距离.（结果精确到0.1 m；参考数据：sin50°≈0.77，cos50°≈0.64，tan50°≈1.19）
　　　　　　

答案：
解：如图，延长AD交CF于点G。
　　　　　　　　
∵DE//GF，DG//EF，
∴四边形DGFE是平行四边形。
∴GF = DE = 1 m。
由题意，知∠ABC = 50°，∠AGC = 45°。
在Rt△ACG中，CG = $\frac{AC}{\tan\angle AGC}$ = $\frac{4}{\tan 45°}$ = 4(m)。
∴CF = CG + GF = 5 m。
在Rt△ABC中，CB = $\frac{AC}{\tan\angle ABC}$ = $\frac{4}{\tan 50°}$≈3.36(m)。
∴BF = CF - CB≈1.6 m，即修改后爬梯底部F与修改前爬梯底部B之间的距离约为1.6 m。

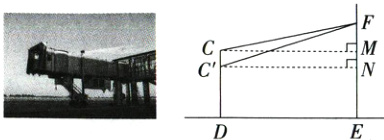
9. 登机桥是用以连接候机厅与飞机之间的可移动升降通道，一端连接候机楼的某个登机口，一端扣在飞机舱门上，当飞机停靠后，登机桥通过调节桥头高度匹配舱门. 如图，飞机停靠在与航站楼FE距离为25 m的D处(DE=25 m)，现需将登机桥头的位置从C处调整到C'处，若调整前后登机桥与水平面的夹角的度数分别为∠FCM=10°，∠FC'N=18°，则登机桥头调节的高度CC'约为________m.（参考数据：sin10°≈0.17，cos10°≈0.98，tan10°≈0.18，sin18°≈0.31，cos18°≈0.95，tan18°≈0.32）
　　

答案： 3.5 解析 由题意，知∠CMF = ∠C'NF = 90°，CM = C'N = DE = 25 m，CC' = MN。
在Rt△CMF中，FM = CMtan∠FCM = 25tan10°≈4.5(m)。
在Rt△C'NF中，FN = C'Ntan∠FC'N = 25tan18°≈8(m)。
∴CC' = MN = FN - FM≈3.5 m，即登机桥头调节的高度CC'约为3.5 m。

10. 数学社团的同学们欲测量某广场上塔的高度. 如图，他们在第一层看台ED上架设测角仪EF，从F处测得塔的最高点A的仰角为42°，测得DE=BC=23 m，斜坡CD长20 m，其坡角为30°，测角仪EF的高度为1.5 m，则塔AB的高度约为________m.（结果精确到0.1；参考数据：sin42°≈0.67，cos42°≈0.74，tan42°≈0.9，$\sqrt{3}$≈1.73）
　　　　　　　　　　　

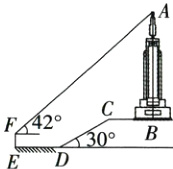
答案：
48.5 解析 如图，过点C作CM⊥ED交ED的延长线于点M，延长AB，ED交于点G，过点F作FH//ED交AG于点H，则∠CMD = ∠AHF = 90°，∠CDM = 30°，∠AFH = 42°，MG = BC = 23 m，GH = EF = 1.5 m，FH = EG，BG = CM。
　　　　　　　
在Rt△CDM中，CM = $\frac{1}{2}$CD = 10 m，DM = CDcos∠CDM = $10\sqrt{3}$ m。
∴BG = 10 m，EG = DE + DM + MG = 23 + $10\sqrt{3}$ + 23≈63.3(m)。
∴FH≈63.3 m。
在Rt△AFH中，AH = FHtan∠AFH≈63.3tan42°≈56.97(m)。
∴AB = AH + HG - BG≈48.5 m，即塔AB的高度约为48.5 m。

11. 如图，在南北方向的海岸线MN上，有A，B两艘巡逻船，现均收到故障船C的求救信号. 已知A，B两船相距100($\sqrt{3}$ + 1)海里，船C在船A的北偏东60°方向上，在船B的东南方向上. MN上有一观测点D，测得船C在观测点D的南偏东75°方向上.
　(1)求AC的长；
　(2)已知距离观测点D处100海里范围内有暗礁，若巡逻船A沿直线AC去营救船C，则在去营救的途中有无触礁危险?（参考数据：$\sqrt{3}$≈1.73）
　　　　　　　　　　　　　

答案：
解：
(1)根据题意，得∠CAB = 60°，∠ABC = 45°，∠ADC = 75°。
如图，过点C作CE⊥AB于点E，则∠CEA = ∠CEB = 90°。
设AE = x海里，则CE = AEtan∠CAE = $\sqrt{3}x$。
∴BE = $\frac{CE}{\tan\angle CBE}$ = $\sqrt{3}x$。
∵AE + BE = AB，
∴x + $\sqrt{3}x$ = 100($\sqrt{3}+1$)，解得x = 100。
∴AC = $\frac{AE}{\cos\angle CAB}$ = 200海里。
　　　　　　　　　
(2)如图，过点D作DF⊥AC于点F，则∠AFD = 90°。
∵∠ACB = 180° - ∠CAB - ∠ABC = 75°，
∴∠ADC = ∠ACB。
又
∵∠CAD = ∠BAC，
∴△ACD∽△ABC。
∴$\frac{AD}{AC}$ = $\frac{AC}{AB}$，即$\frac{AD}{200}$ = $\frac{200}{100(\sqrt{3}+1)}$。
∴AD = $\frac{400}{\sqrt{3}+1}$海里。
∴DF = ADsin∠DAF≈127 ＞ 100。
∴在去营救的途中无触礁危险。