2025年名校作业九年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年名校作业九年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
1. 如图,一座厂房屋顶人字架的上弦AB=BC=5 m,∠BAC=26°. 若用状态设定为“度”的计算器求屋顶人字架的高BD,则下列按键顺序正确的是( )

A. 5 ÷ tan 2 6 =
B. 5 × sin 2 6 =
C. 5 × cos 2 6 =
D. 5 × tan 2 6 =

A. 5 ÷ tan 2 6 =
B. 5 × sin 2 6 =
C. 5 × cos 2 6 =
D. 5 × tan 2 6 =
答案:
B
2. 用计算器求下列各式的值(精确到0.000 1):
(1)cos20.72°≈________;
(2)cos25°18′≈________;
(3)sin27°16′≈________;
(4)sin18°+cos55°-tan59°≈________.
(1)cos20.72°≈________;
(2)cos25°18′≈________;
(3)sin27°16′≈________;
(4)sin18°+cos55°-tan59°≈________.
答案:
(1)0.9353
(2)0.9041
(3)0.4581
(4)−0.7817
(1)0.9353
(2)0.9041
(3)0.4581
(4)−0.7817
3. 如图,光线与地面的夹角为50°,篮球在地面上的投影AB=32 cm,求这个篮球的直径. (结果精确到0.01 cm)


答案:
解:如图,过点A作AC⊥BF,垂足为点C,则篮球的直径等于AC的长度 .
.
由题意,得∠ABC = 50°.
∴这个篮球的直径为AB·sin50° = 32sin50°≈24.51(cm).
解:如图,过点A作AC⊥BF,垂足为点C,则篮球的直径等于AC的长度
 .
.由题意,得∠ABC = 50°.
∴这个篮球的直径为AB·sin50° = 32sin50°≈24.51(cm).
4. 一辆小车沿着如图所示的斜坡向上行驶了100米,其铅直高度上升了15米. 在用状态设定为“度”的计算器求∠α的度数时,具体按键顺序是( )
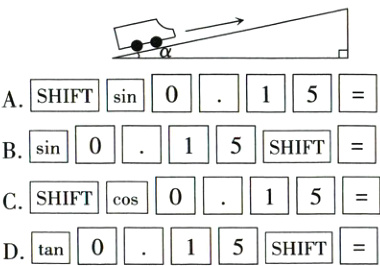
A. SHIFT sin 0. 1 5 =
B. sin 0. 1 5 SHIFT =
C. SHIFT cos 0. 1 5 =
D. tan 0. 1 5 SHIFT =

A. SHIFT sin 0. 1 5 =
B. sin 0. 1 5 SHIFT =
C. SHIFT cos 0. 1 5 =
D. tan 0. 1 5 SHIFT =
答案:
A
5. 根据条件求下列锐角的度数(精确到1′):
(1)sinA=0.675,∠A≈________;
(2)cosB=0.078 9,∠B≈________;
(3)tanC=35.6,∠C≈________.
(1)sinA=0.675,∠A≈________;
(2)cosB=0.078 9,∠B≈________;
(3)tanC=35.6,∠C≈________.
答案:
(1)42°27′
(2)85°28′
(3)88°23'
(1)42°27′
(2)85°28′
(3)88°23'
6. 某校数学“综合与实践”小组的同学想要测量校园内文化长廊(如图①)的最高点到地面的高度. 图②是其测量示意图,五边形ABDEC关于直线EF对称,EF与AB,CD分别相交于点F,G. 测得AB=3 m,CD=5 m,∠ABD=135°,∠BDE=92°,则文化长廊的最高点离地面的高度EF约为________m.(精确到0.1 m)
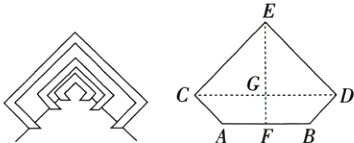

答案:
3.7 解析:
∵五边形ABDEC关于直线EF对称,
∴AF = BF = $\frac{1}{2}$AB = 1.5 m,DG = CG = $\frac{1}{2}$CD = 2.5 m,CD//AB.
∴∠ABD + ∠BDG = 180°.
∴∠BDG = 45°.
∴∠EDG = ∠BDE - ∠BDG = 47°.
如图,过点B作BH⊥CD于点H,则四边形GFBH为矩形,∠BHD = 90°.
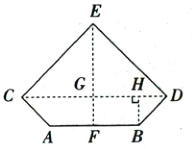
∴GF = BH,GH = BF = 1.5 m.
∴DH = DG - GH = 1 m.
在Rt△BDH中,BH = DHtan∠BDH = 1 m,
∴GF = 1 m.
在Rt△DGE中,EG = DGtan∠EDG = 2.5tan47°≈2.7(m).
∴EF = EG + GF≈3.7 m.
3.7 解析:
∵五边形ABDEC关于直线EF对称,
∴AF = BF = $\frac{1}{2}$AB = 1.5 m,DG = CG = $\frac{1}{2}$CD = 2.5 m,CD//AB.
∴∠ABD + ∠BDG = 180°.
∴∠BDG = 45°.
∴∠EDG = ∠BDE - ∠BDG = 47°.
如图,过点B作BH⊥CD于点H,则四边形GFBH为矩形,∠BHD = 90°.

∴GF = BH,GH = BF = 1.5 m.
∴DH = DG - GH = 1 m.
在Rt△BDH中,BH = DHtan∠BDH = 1 m,
∴GF = 1 m.
在Rt△DGE中,EG = DGtan∠EDG = 2.5tan47°≈2.7(m).
∴EF = EG + GF≈3.7 m.
7. (1)用计算器判断sin25°+sin46°与sin71°之间的大小关系;
(2)若α,β,α+β都是锐角,猜想sinα+sinβ与sin(α+β)的大小关系;
(3)请借助如图所示的图形证明(2)的猜想.

(2)若α,β,α+β都是锐角,猜想sinα+sinβ与sin(α+β)的大小关系;
(3)请借助如图所示的图形证明(2)的猜想.

答案:
(1)解:sin25° + sin46°≈0.4226 + 0.7193≈1.142,sin71°≈0.946,
∵1.142>0.946,
∴sin25° + sin46°>sin71°.
(2)sinα + sinβ>sin(α + β).
(3)证明:sinα + sinβ = $\frac{AB}{OA}$ + $\frac{BC}{OB}$,
sin(α + β) = $\frac{AE}{OA}$,
∵OA>OB,
∴ $\frac{BC}{OB}$ > $\frac{BC}{OA}$.
∴ $\frac{AB}{OA}$ + $\frac{BC}{OB}$ > $\frac{AB}{OA}$ + $\frac{BC}{OA}$ = $\frac{AB + BC}{OA}$.
如图,连接AC.
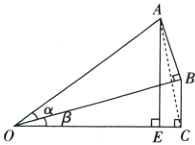
∵AB + BC>AC>AE,
∴ $\frac{AB + BC}{OA}$ > $\frac{AE}{OA}$.
∴ $\frac{AB}{OA}$ + $\frac{BC}{OB}$ > $\frac{AE}{OA}$,
即sinα + sinβ>sin(α + β).
(1)解:sin25° + sin46°≈0.4226 + 0.7193≈1.142,sin71°≈0.946,
∵1.142>0.946,
∴sin25° + sin46°>sin71°.
(2)sinα + sinβ>sin(α + β).
(3)证明:sinα + sinβ = $\frac{AB}{OA}$ + $\frac{BC}{OB}$,
sin(α + β) = $\frac{AE}{OA}$,
∵OA>OB,
∴ $\frac{BC}{OB}$ > $\frac{BC}{OA}$.
∴ $\frac{AB}{OA}$ + $\frac{BC}{OB}$ > $\frac{AB}{OA}$ + $\frac{BC}{OA}$ = $\frac{AB + BC}{OA}$.
如图,连接AC.

∵AB + BC>AC>AE,
∴ $\frac{AB + BC}{OA}$ > $\frac{AE}{OA}$.
∴ $\frac{AB}{OA}$ + $\frac{BC}{OB}$ > $\frac{AE}{OA}$,
即sinα + sinβ>sin(α + β).
查看更多完整答案,请扫码查看


