2025年53精准练九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
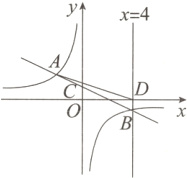
7. 如图,一次函数$y = kx + b(k\neq0)$的图象与反比例函数$y = -\frac{4}{x}$的图象交于点$A(-2,m)$和点$B$,与$y$轴交于点$C$.直线$x = 4$经过点$B$,与$x$轴交于点$D$,连接$AD$.
(1)求$k$、$b$的值;
(2)求$\triangle ABD$的面积;
(3)直接写出一个一次函数的表达式,使它的图象经过点$C$且$y$随$x$的增大而增大.
(1)求$k$、$b$的值;
(2)求$\triangle ABD$的面积;
(3)直接写出一个一次函数的表达式,使它的图象经过点$C$且$y$随$x$的增大而增大.

答案:
解:
(1)设B(4,n),把A(−2,m),B(4,n)代入y=−$\frac{4}{x}$,得−$\frac{4}{−2}$=m,−$\frac{4}{4}$=n,
解得m = 2,n = -1,
∴A(-2, 2),B(4, -1),
把A(-2, 2),B(4, -1)代入y = kx + b中,
得$\begin{cases}-2k + b = 2\\4k + b = -1\end{cases}$,解得$\begin{cases}k = -\frac{1}{2}\\b = 1\end{cases}$.
(2)由题意可知D(4,0),
∴△ABD的面积为$\frac{1}{2}$×1×(4 + 2)=3.
(3)满足条件的一次函数表达式为y= x+1(答案不唯一).
(1)设B(4,n),把A(−2,m),B(4,n)代入y=−$\frac{4}{x}$,得−$\frac{4}{−2}$=m,−$\frac{4}{4}$=n,
解得m = 2,n = -1,
∴A(-2, 2),B(4, -1),
把A(-2, 2),B(4, -1)代入y = kx + b中,
得$\begin{cases}-2k + b = 2\\4k + b = -1\end{cases}$,解得$\begin{cases}k = -\frac{1}{2}\\b = 1\end{cases}$.
(2)由题意可知D(4,0),
∴△ABD的面积为$\frac{1}{2}$×1×(4 + 2)=3.
(3)满足条件的一次函数表达式为y= x+1(答案不唯一).
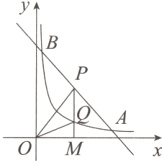
8. 如图,一次函数$y_1 = kx + b(k\neq0)$的图象与反比例函数$y_2 = \frac{m}{x}(x > 0)$的图象交于$A(4,1)$,$B(\frac{1}{2},a)$两点.
(1)求这两个函数的表达式;
(2)根据图象,直接写出满足$y_1 - y_2 > 0$时$x$的取值范围;
(3)点$P$在线段$AB$上,过点$P$作$x$轴的垂线,垂足为$M$,交函数$y_2$的图象于点$Q$,若$\triangle POQ$的面积为3,求点$P$的坐标.
(1)求这两个函数的表达式;
(2)根据图象,直接写出满足$y_1 - y_2 > 0$时$x$的取值范围;
(3)点$P$在线段$AB$上,过点$P$作$x$轴的垂线,垂足为$M$,交函数$y_2$的图象于点$Q$,若$\triangle POQ$的面积为3,求点$P$的坐标.

答案:
解:
(1)
∵反比例函数y2 = $\frac{m}{x}$(x>0)的图象经过点A(4,1),
∴1 = $\frac{m}{4}$,
∴m = 4.
∴反比例函数的表达式为y2 = $\frac{4}{x}$(x>0).
把B($\frac{1}{2}$,a)代入y2 = $\frac{4}{x}$(x>0),得a=8.
∴点B的坐标为($\frac{1}{2}$,8),
∵一次函数y1 = kx+b的图象经过A(4,1),B($\frac{1}{2}$,8),
∴$\begin{cases}4k + b = 1\\\frac{1}{2}k + b = 8\end{cases}$,
∴$\begin{cases}k = -2\\b = 9\end{cases}$.
故一次函数的表达式为y1 = -2x+9.
(2)$\frac{1}{2}$<x<4.
(3)由题意设P(p,−2p+9),$\frac{1}{2}$<p<4,
则Q(p,$\frac{4}{p}$).
∴PQ=−2p+9−$\frac{4}{p}$.
∴S△POQ = $\frac{1}{2}$(-2p + 9 - $\frac{4}{p}$)·p = 3.
∴p1 = $\frac{5}{2}$,p2 = 2.
∴点P的坐标为($\frac{5}{2}$,4)或(2,5).
(1)
∵反比例函数y2 = $\frac{m}{x}$(x>0)的图象经过点A(4,1),
∴1 = $\frac{m}{4}$,
∴m = 4.
∴反比例函数的表达式为y2 = $\frac{4}{x}$(x>0).
把B($\frac{1}{2}$,a)代入y2 = $\frac{4}{x}$(x>0),得a=8.
∴点B的坐标为($\frac{1}{2}$,8),
∵一次函数y1 = kx+b的图象经过A(4,1),B($\frac{1}{2}$,8),
∴$\begin{cases}4k + b = 1\\\frac{1}{2}k + b = 8\end{cases}$,
∴$\begin{cases}k = -2\\b = 9\end{cases}$.
故一次函数的表达式为y1 = -2x+9.
(2)$\frac{1}{2}$<x<4.
(3)由题意设P(p,−2p+9),$\frac{1}{2}$<p<4,
则Q(p,$\frac{4}{p}$).
∴PQ=−2p+9−$\frac{4}{p}$.
∴S△POQ = $\frac{1}{2}$(-2p + 9 - $\frac{4}{p}$)·p = 3.
∴p1 = $\frac{5}{2}$,p2 = 2.
∴点P的坐标为($\frac{5}{2}$,4)或(2,5).
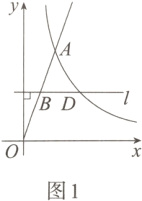
9. [2024济南]已知反比例函数$y = \frac{k}{x}(x > 0)$的图象与正比例函数$y = 3x(x\geq0)$的图象交于点$A(2,a)$,点$B$是线段$OA$上(不与点$A$重合)的一点.
(1)求反比例函数的表达式;
(2)如图1,过点$B$作$y$轴的垂线$l$,$l$与$y = \frac{k}{x}(x > 0)$的图象交于点$D$,当线段$BD = 3$时,求点$B$的坐标;
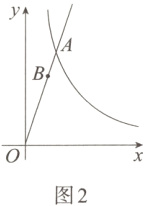
(3)如图2,将点$A$绕点$B$顺时针旋转$90^{\circ}$得到点$E$,当点$E$恰好落在$y = \frac{k}{x}(x > 0)$的图象上时,求点$E$的坐标.
(1)求反比例函数的表达式;
(2)如图1,过点$B$作$y$轴的垂线$l$,$l$与$y = \frac{k}{x}(x > 0)$的图象交于点$D$,当线段$BD = 3$时,求点$B$的坐标;
(3)如图2,将点$A$绕点$B$顺时针旋转$90^{\circ}$得到点$E$,当点$E$恰好落在$y = \frac{k}{x}(x > 0)$的图象上时,求点$E$的坐标.


答案:
解:
(1)将A(2,a)代入y=3x,
得a=3×2=6,
∴A(2,6),
将A(2,6)代入y=$\frac{k}{x}$得6 = $\frac{k}{2}$,
解得k = 12,
∴反比例函数的表达式为y=$\frac{12}{x}$.
(2)设点B(m,3m),则点D(m + 3,3m),
由y=$\frac{12}{x}$可得xy=12,
∴3m(m + 3)=12,
解得m1 = 1,m2 = -4(舍去),
∴B(1,3).
(3)如图,过点B作y轴的平行线,分别过点E、点A作x轴的平行线,交点分别为H、F,则∠EHB = ∠BFA = 90°,

连接BE,
∴∠HEB + ∠EBH = 90°,
∵将点A绕点B顺时针旋转90°得到点E,
∴∠ABE = 90°,BE = BA,
∴∠EBH + ∠ABF = 90°,
∴∠BEH = ∠ABF,
∴△EHB≌△BFA(AAS).
设点B(n,3n),则EH = BF = 6 - 3n,
BH = AF = 2 - n,
∴E(6 - 2n,4n - 2),
∵点E在反比例函数图象上,
∴(4n - 2)(6 - 2n)=12,
解得n1 = $\frac{3}{2}$,n2 = 2(舍去).
∴E(3,4).
解:
(1)将A(2,a)代入y=3x,
得a=3×2=6,
∴A(2,6),
将A(2,6)代入y=$\frac{k}{x}$得6 = $\frac{k}{2}$,
解得k = 12,
∴反比例函数的表达式为y=$\frac{12}{x}$.
(2)设点B(m,3m),则点D(m + 3,3m),
由y=$\frac{12}{x}$可得xy=12,
∴3m(m + 3)=12,
解得m1 = 1,m2 = -4(舍去),
∴B(1,3).
(3)如图,过点B作y轴的平行线,分别过点E、点A作x轴的平行线,交点分别为H、F,则∠EHB = ∠BFA = 90°,

连接BE,
∴∠HEB + ∠EBH = 90°,
∵将点A绕点B顺时针旋转90°得到点E,
∴∠ABE = 90°,BE = BA,
∴∠EBH + ∠ABF = 90°,
∴∠BEH = ∠ABF,
∴△EHB≌△BFA(AAS).
设点B(n,3n),则EH = BF = 6 - 3n,
BH = AF = 2 - n,
∴E(6 - 2n,4n - 2),
∵点E在反比例函数图象上,
∴(4n - 2)(6 - 2n)=12,
解得n1 = $\frac{3}{2}$,n2 = 2(舍去).
∴E(3,4).
查看更多完整答案,请扫码查看


