2025年53精准练九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
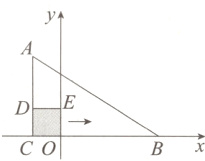
1. 如图,在△ABC中,∠ACB = 90°,边BC在x轴上,顶点A,B的坐标分别为(-2,8)和(10,0).将正方形OCDE沿x轴向右平移,当点E落在AB边上时,点D的坐标为__________.

答案:
(5, 2)
详解:如图,设正方形D'C'O'E'是正方形OCDE沿x轴向右平移后的正方形,
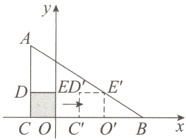
∵顶点A,B的坐标分别为(-2, 8)和(10, 0),
∴AC = 8,OC = 2,OB = 10,
∴BC = 12,
∵四边形OCDE是正方形,
∴DE = OC = OE = 2,
∴O'E' = O'C' = C'D' = 2,
∵E'O'⊥BC,
∴∠BO'E' = ∠BCA = 90°,
∴E'O'//AC,
∴△BO'E'∽△BCA,
∴$\frac{E'O'}{AC}=\frac{BO'}{BC}$,
∴$\frac{2}{8}=\frac{BO'}{12}$,
∴BO' = 3,
∴OC' = 10 - 2 - 3 = 5,
∴当点E落在AB边上时,点D的坐标为(5, 2).
(5, 2)
详解:如图,设正方形D'C'O'E'是正方形OCDE沿x轴向右平移后的正方形,

∵顶点A,B的坐标分别为(-2, 8)和(10, 0),
∴AC = 8,OC = 2,OB = 10,
∴BC = 12,
∵四边形OCDE是正方形,
∴DE = OC = OE = 2,
∴O'E' = O'C' = C'D' = 2,
∵E'O'⊥BC,
∴∠BO'E' = ∠BCA = 90°,
∴E'O'//AC,
∴△BO'E'∽△BCA,
∴$\frac{E'O'}{AC}=\frac{BO'}{BC}$,
∴$\frac{2}{8}=\frac{BO'}{12}$,
∴BO' = 3,
∴OC' = 10 - 2 - 3 = 5,
∴当点E落在AB边上时,点D的坐标为(5, 2).
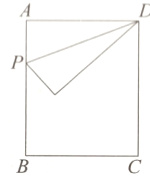
2. 如图,在矩形ABCD中,AB = 4,BC = 3,点P是边AB上一动点,连接DP.
(1)若将△DAP沿DP折叠,点A落在矩形的对角线上的点A'处,求AP的长;
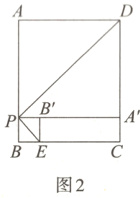
(2)点P运动到某一位置,过点P作直线PE交BC于点E,将△DAP与△PBE分别沿DP与PE折叠,点A与点B分别落在点A',B'处,若P,A',B'三点恰好在同一直线上,且A'B' = 2,求此时AP的长.
(1)若将△DAP沿DP折叠,点A落在矩形的对角线上的点A'处,求AP的长;
(2)点P运动到某一位置,过点P作直线PE交BC于点E,将△DAP与△PBE分别沿DP与PE折叠,点A与点B分别落在点A',B'处,若P,A',B'三点恰好在同一直线上,且A'B' = 2,求此时AP的长.

答案:
解:
(1)①当点A落在对角线BD上时,
设AP = P'A' = x,
在矩形ABCD中,AD = BC = 3,
在Rt△ADB中,
∵AB = 4,AD = 3,
∴BD = $\sqrt{3^{2}+4^{2}}$ = 5,
∵AD = DA' = 3,
∴BA' = 2,
在Rt△BP'A'中,BP'² = P'A'² + BA'²,即(4 - x)² = x² + 2²,解得x = $\frac{3}{2}$,
∴AP = $\frac{3}{2}$.
②当点A落在对角线AC上时,
由翻折的性质可知PD⊥AC,易证△DAP∽△ABC,
∴$\frac{AD}{AP}=\frac{AB}{BC}$,
∴AP = $\frac{AD\cdot BC}{AB}=\frac{3×3}{4}=\frac{9}{4}$.
∴AP的长为$\frac{3}{2}$或$\frac{9}{4}$.
(2)设AP = x,
则PB = 4 - x,
根据折叠的性质可知PA = P'A' = x,PB = PB' = 4 - x.
①当A'在线段PB'上时,如图1,
∵A'B' = 2,
∴4 - x - x = 2,
∴x = 1,即AP = 1.
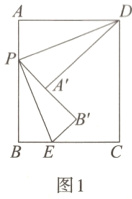
②当B'在线段PA'上时,如图2,
∵A'B' = 2,
∴x - (4 - x) = 2,
∴x = 3,
∴AP = 3.
综上所述,AP的长为1或3.
解:
(1)①当点A落在对角线BD上时,
设AP = P'A' = x,
在矩形ABCD中,AD = BC = 3,
在Rt△ADB中,
∵AB = 4,AD = 3,
∴BD = $\sqrt{3^{2}+4^{2}}$ = 5,
∵AD = DA' = 3,
∴BA' = 2,
在Rt△BP'A'中,BP'² = P'A'² + BA'²,即(4 - x)² = x² + 2²,解得x = $\frac{3}{2}$,
∴AP = $\frac{3}{2}$.
②当点A落在对角线AC上时,
由翻折的性质可知PD⊥AC,易证△DAP∽△ABC,
∴$\frac{AD}{AP}=\frac{AB}{BC}$,
∴AP = $\frac{AD\cdot BC}{AB}=\frac{3×3}{4}=\frac{9}{4}$.
∴AP的长为$\frac{3}{2}$或$\frac{9}{4}$.
(2)设AP = x,
则PB = 4 - x,
根据折叠的性质可知PA = P'A' = x,PB = PB' = 4 - x.
①当A'在线段PB'上时,如图1,
∵A'B' = 2,
∴4 - x - x = 2,
∴x = 1,即AP = 1.

②当B'在线段PA'上时,如图2,
∵A'B' = 2,
∴x - (4 - x) = 2,
∴x = 3,
∴AP = 3.

综上所述,AP的长为1或3.
3. [2024运城三模]综合与实践
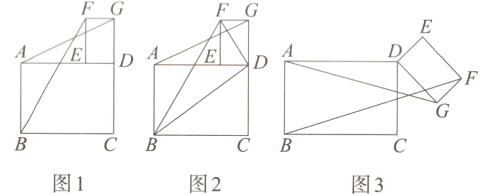
【问题情境】在综合与实践课上,老师让同学们利用准备好的两张矩形纸片进行探究活动.智慧小组准备了两张矩形纸片ABCD和DEFG,其中AB = 6,BC = 8,DE = 3,EF = 4,将它们按如图1所示的方式放置,点E落在AD上,点G落在CD的延长线上,连接AG和BF.
【观察发现】(1)如图2,连接BD,FD,则BD和FD的位置关系是__________,$\frac{AG}{BF}=$__________;
【操作探究】(2)如图3,将矩形DEFG绕点D按顺时针方向旋转$\alpha(0^{\circ}<\alpha<360^{\circ})$,试探究(1)中AG和BF的数量关系是否仍然成立,并说明理由;
【拓展延伸】(3)在矩形DEFG旋转的过程中,当B、G、F三点共线时,直接写出线段AG的长.
【问题情境】在综合与实践课上,老师让同学们利用准备好的两张矩形纸片进行探究活动.智慧小组准备了两张矩形纸片ABCD和DEFG,其中AB = 6,BC = 8,DE = 3,EF = 4,将它们按如图1所示的方式放置,点E落在AD上,点G落在CD的延长线上,连接AG和BF.
【观察发现】(1)如图2,连接BD,FD,则BD和FD的位置关系是__________,$\frac{AG}{BF}=$__________;
【操作探究】(2)如图3,将矩形DEFG绕点D按顺时针方向旋转$\alpha(0^{\circ}<\alpha<360^{\circ})$,试探究(1)中AG和BF的数量关系是否仍然成立,并说明理由;
【拓展延伸】(3)在矩形DEFG旋转的过程中,当B、G、F三点共线时,直接写出线段AG的长.

答案:
解:
(1)BD⊥FD;$\frac{4}{5}$.
详解:如图,延长GF、BA相交于H,
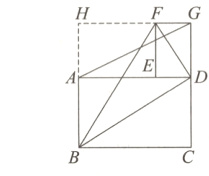
∵四边形ABCD和四边形DEFG都是矩形,
∴BH//CG,GH//BC,∠H = 90°,
AH = EF = 4,GH = BC = 8,BH = AB + AH = 10,FH = HG - GF = 5,
由勾股定理得,
BF = $\sqrt{BH^{2}+FH^{2}}=\sqrt{10^{2}+5^{2}}$ = 5$\sqrt{5}$,
BD = $\sqrt{BC^{2}+CD^{2}}=\sqrt{8^{2}+6^{2}}$ = 10,
DF = $\sqrt{DG^{2}+FG^{2}}=\sqrt{4^{2}+3^{2}}$ = 5,
AG = $\sqrt{DG^{2}+AD^{2}}=\sqrt{4^{2}+8^{2}}$ = 4$\sqrt{5}$,
∴$\frac{AG}{BF}=\frac{4}{5}$,
易得BD² + DF² = BF²,
∴△BDF是直角三角形,
∴BD⊥FD.
(2)成立.
理由:如图,连接BD和DF.
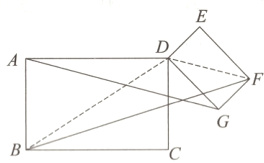
∵四边形ABCD是矩形,AB = 6,BC = 8,
∴AD = BC = 8,∠DAB = 90°,
∴BD = $\sqrt{AB^{2}+AD^{2}}$ = 10,
∵四边形DEFG是矩形,DE = 3,EF = 4,
∴GF = DE = 3,DG = EF = 4,∠DGF = 90°,
∴DF = $\sqrt{DG^{2}+GF^{2}}$ = 5,
∵$\frac{AB}{GF}=\frac{6}{3}$ = 2,$\frac{AD}{DG}=\frac{8}{4}$ = 2,
∴$\frac{AB}{GF}=\frac{AD}{DG}$.
∵∠BAD = ∠DGF = 90°,
∴△ABD∽△GFD,
∴∠BDA = ∠GDF,
∴∠BDA + ∠BDG = ∠GDF + ∠BDG,
∴∠ADG = ∠BDF,
∵$\frac{AD}{BD}=\frac{8}{10}=\frac{4}{5}$,$\frac{DG}{DF}=\frac{4}{5}$,
∴$\frac{AD}{BD}=\frac{DG}{DF}$,
∴△ADG∽△BDF,
∴$\frac{AG}{BF}=\frac{AD}{BD}=\frac{4}{5}$.
(3)AG的长为$\frac{8\sqrt{21}+12}{5}$或$\frac{8\sqrt{21}-12}{5}$.
详解:①当点F在BG的延长线上时,连接BD,
∵∠DGF = 90°,
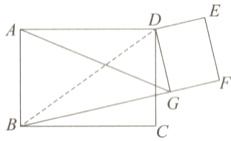
∴∠BGD = 90°,
∴△DBG为直角三角形,
∴BG² = BD² - DG² = 100 - 16 = 84,
∴BG = 2$\sqrt{21}$(负值舍去),
∴BF = BG + GF = 2$\sqrt{21}$ + 3.
由
(2)得$\frac{AG}{BF}=\frac{4}{5}$,
∴AG = $\frac{8\sqrt{21}+12}{5}$.
②当点F在线段BG上时,连接BD,

∵∠BGD = 90°,
∴△DBG为直角三角形,
∴ = BD² - DG² = 100 - 16 = 84,
∴BG = 2$\sqrt{21}$(负值舍去),
∴BF = BG - GF = 2$\sqrt{21}$ - 3.
由
(2)得$\frac{AG}{BF}=\frac{4}{5}$,
∴AG = $\frac{8\sqrt{21}-12}{5}$.
综上所述,当B、G、F三点共线时,线段AG的长为$\frac{8\sqrt{21}+12}{5}$或$\frac{8\sqrt{21}-12}{5}$.
解:
(1)BD⊥FD;$\frac{4}{5}$.
详解:如图,延长GF、BA相交于H,

∵四边形ABCD和四边形DEFG都是矩形,
∴BH//CG,GH//BC,∠H = 90°,
AH = EF = 4,GH = BC = 8,BH = AB + AH = 10,FH = HG - GF = 5,
由勾股定理得,
BF = $\sqrt{BH^{2}+FH^{2}}=\sqrt{10^{2}+5^{2}}$ = 5$\sqrt{5}$,
BD = $\sqrt{BC^{2}+CD^{2}}=\sqrt{8^{2}+6^{2}}$ = 10,
DF = $\sqrt{DG^{2}+FG^{2}}=\sqrt{4^{2}+3^{2}}$ = 5,
AG = $\sqrt{DG^{2}+AD^{2}}=\sqrt{4^{2}+8^{2}}$ = 4$\sqrt{5}$,
∴$\frac{AG}{BF}=\frac{4}{5}$,
易得BD² + DF² = BF²,
∴△BDF是直角三角形,
∴BD⊥FD.
(2)成立.
理由:如图,连接BD和DF.

∵四边形ABCD是矩形,AB = 6,BC = 8,
∴AD = BC = 8,∠DAB = 90°,
∴BD = $\sqrt{AB^{2}+AD^{2}}$ = 10,
∵四边形DEFG是矩形,DE = 3,EF = 4,
∴GF = DE = 3,DG = EF = 4,∠DGF = 90°,
∴DF = $\sqrt{DG^{2}+GF^{2}}$ = 5,
∵$\frac{AB}{GF}=\frac{6}{3}$ = 2,$\frac{AD}{DG}=\frac{8}{4}$ = 2,
∴$\frac{AB}{GF}=\frac{AD}{DG}$.
∵∠BAD = ∠DGF = 90°,
∴△ABD∽△GFD,
∴∠BDA = ∠GDF,
∴∠BDA + ∠BDG = ∠GDF + ∠BDG,
∴∠ADG = ∠BDF,
∵$\frac{AD}{BD}=\frac{8}{10}=\frac{4}{5}$,$\frac{DG}{DF}=\frac{4}{5}$,
∴$\frac{AD}{BD}=\frac{DG}{DF}$,
∴△ADG∽△BDF,
∴$\frac{AG}{BF}=\frac{AD}{BD}=\frac{4}{5}$.
(3)AG的长为$\frac{8\sqrt{21}+12}{5}$或$\frac{8\sqrt{21}-12}{5}$.
详解:①当点F在BG的延长线上时,连接BD,
∵∠DGF = 90°,

∴∠BGD = 90°,
∴△DBG为直角三角形,
∴BG² = BD² - DG² = 100 - 16 = 84,
∴BG = 2$\sqrt{21}$(负值舍去),
∴BF = BG + GF = 2$\sqrt{21}$ + 3.
由
(2)得$\frac{AG}{BF}=\frac{4}{5}$,
∴AG = $\frac{8\sqrt{21}+12}{5}$.
②当点F在线段BG上时,连接BD,

∵∠BGD = 90°,
∴△DBG为直角三角形,
∴ = BD² - DG² = 100 - 16 = 84,
∴BG = 2$\sqrt{21}$(负值舍去),
∴BF = BG - GF = 2$\sqrt{21}$ - 3.
由
(2)得$\frac{AG}{BF}=\frac{4}{5}$,
∴AG = $\frac{8\sqrt{21}-12}{5}$.
综上所述,当B、G、F三点共线时,线段AG的长为$\frac{8\sqrt{21}+12}{5}$或$\frac{8\sqrt{21}-12}{5}$.
查看更多完整答案,请扫码查看


