《2025年53精准练九年级数学下册人教版山西专版》

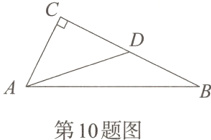
10. 如图，在Rt△ABC中，∠C = 90°，D是BC的中点，AC = 6，tan∠ABC = $\frac{1}{2}$，则BD =（ ）

A. 8
B. 6
C. 4
D. 3

答案： B

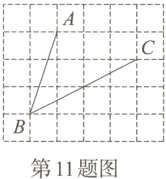
11. [2023运城盐湖区期末] 如图，在5×6的正方形网格中，点A，B，C都在格点上，则tan∠ABC的值为（ ）

A. $\frac{\sqrt{2}}{2}$
B. $\sqrt{2}$
C. 1
D. $\frac{\sqrt{3}}{3}$

答案： C

12. [2023大同云州区期末] 如图，在Rt△ABC中，∠ACB = 90°，D是AB的中点，连接CD，过点B作CD的垂线，交CD的延长线于点E，tan A = $\frac{4}{3}$，则cos∠DBE的值为__________.

答案： $\frac{24}{25}$

13. 在矩形ABCD中，AB = 10，BC = 8，E为边AD上一点，沿CE将△CDE翻折，使点D正好落在AB边上的点F处，求tan∠AFE的值.

答案： 解：由题意可知∠AFE + ∠EFC + ∠BFC = 180°.
由折叠的性质，得∠EFC = ∠EDC = 90°，所以∠AFE + ∠BFC = 90°，
在Rt△BCF中，∠BCF + ∠BFC = 90°，
所以∠AFE = ∠BCF.
在Rt△BFC中，BC = 8，根据矩形和折叠的性质，得CF = CD = AB = 10，
由勾股定理可得BF = $\sqrt{CF^{2}-BC^{2}} = 6$，
则tan∠BCF = $\frac{BF}{BC}=\frac{3}{4}$，
所以tan∠AFE = tan∠BCF = $\frac{3}{4}$.

14. [2024银川模拟] 如图，PA，PB分别与⊙O相切于A，B两点，AC是⊙O的直径. 连接PO交⊙O于点D，交AB于点H.
(1) 求证：∠BAC = $\frac{1}{2}$∠APB；
(2) 若AC = 6，cos∠BAC = $\frac{4}{5}$，求PD的长.

答案：
解：
(1)证明：连接OB，

∵PA，PB分别与⊙O相切于A，B两点，
∴PA = PB，OA⊥PA，OB⊥PB，
∵OA = OB，
∴PO平分∠APB，
∴∠APO = $\frac{1}{2}$∠APB，PO⊥AB，
∴∠OAH + ∠PAH = ∠APH + ∠PAH = 90°，
∴∠BAC = ∠APH = $\frac{1}{2}$∠APB.
(2)
∵∠APO = ∠BAC，
∴cos∠APO = cos∠BAC = $\frac{4}{5}$，
∴$\frac{AP}{PO}=\frac{4}{5}$，
设AP = 4x，则PO = 5x，
∵∠PAO = 90°，
∴AO = $\sqrt{PO^{2}-AP^{2}} = 3x$，
∵AC = 2AO = 6，
∴3x = 3，
∴x = 1，
∴PO = 5x = 5，AO = OD = 3x = 3，
∴PD = PO - OD = 5 - 3 = 2.

15. [推理能力·2024运城期末] 如图，已知l1//l2//l3，相邻两条平行直线间的距离相等，△ABC的三个顶点分别在这三条平行直线上，且∠ACB = 90°，∠CAB = 45°，则tan α的值是__________.

答案：
$\frac{1}{3}$
详解：如图，过点A作l₁的垂线，垂足为D，过点B分别作l₁、l₃的垂线，垂足分别为E、F.

设l₁、l₂之间的距离为a，则l₂与l₃之间的距离也为a.
∵∠ACB = 90°，∠CAB = 45°，
∴∠DCA + ∠ECB = 90°，AC = CB，
∵∠DCA + ∠DAC = 90°，
∴∠DAC = ∠ECB，
∵∠ADC = ∠CEB，AC = CB，
∴△ADC≌△CEB(AAS)，
∴CE = AD = 2a，DC = EB = a，
∴易得AF = DE = 3a，
∵BF = a，
∴tanα = $\frac{BF}{AF}=\frac{1}{3}$.