2025年53精准练九年级数学下册人教版山西专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年53精准练九年级数学下册人教版山西专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
7.如图,矩形OABC与矩形ODEF是位似图形,点P是位似中心.若点B的坐标为(2,3),点E的横坐标为 - 1,则点P的坐标为 ( )
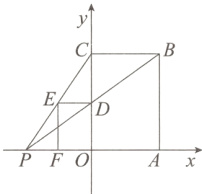
A.(-2,0)
B.(0,-2)
C.(- $\frac{3}{2}$,0)
D.(0,- $\frac{3}{2}$)

A.(-2,0)
B.(0,-2)
C.(- $\frac{3}{2}$,0)
D.(0,- $\frac{3}{2}$)
答案:
A
8.如图,在平面直角坐标系中,△ABC的顶点坐标分别为(4,0),(8,2),(6,4).已知△A1B1C1的两个顶点的坐标为(1,3),(2,5),若△ABC与△A1B1C1位似,则△A1B1C1的第三个顶点的坐标为______________.


答案:
(0, 4)或(3, 4)
9.如图,在平面直角坐标系中,点A,B的坐标分别为(3,0),(2, - 3),△AB'O'是△ABO关于点A的位似图形.已知点O'的坐标为(-1,0),求点B'的坐标.


答案:
解: 过点B作BE⊥x轴于点E, 过点B'作B'F⊥x轴于点F,
∵点A, B的坐标分别为(3, 0), (2, -3), 点O'的坐标为(-1, 0),
∴AO = 3, AO' = 4, EO = 2, BE = 3,
∵△AB'O'是△ABO关于点A的位似图形,
∴$\frac{AO}{AO'}=\frac{AB}{AB'}=\frac{3}{4}$,
由BE⊥x轴, B'F⊥x轴,
易知△ABE∽△AB'F,
∴$\frac{AE}{AF}=\frac{BE}{B'F}=\frac{AB}{AB'}=\frac{3}{4}$,
∵AE = AO - EO = 1,
∴$\frac{1}{AF}=\frac{3}{4}$,
∴AF = $\frac{4}{3}$.
∴FO = 3 - $\frac{4}{3}=\frac{5}{3}$.
∵$\frac{BE}{B'F}=\frac{3}{B'F}=\frac{3}{4}$,
∴B'F = 4,
∴点B'的坐标为($\frac{5}{3}$, -4).

解: 过点B作BE⊥x轴于点E, 过点B'作B'F⊥x轴于点F,
∵点A, B的坐标分别为(3, 0), (2, -3), 点O'的坐标为(-1, 0),
∴AO = 3, AO' = 4, EO = 2, BE = 3,
∵△AB'O'是△ABO关于点A的位似图形,
∴$\frac{AO}{AO'}=\frac{AB}{AB'}=\frac{3}{4}$,
由BE⊥x轴, B'F⊥x轴,
易知△ABE∽△AB'F,
∴$\frac{AE}{AF}=\frac{BE}{B'F}=\frac{AB}{AB'}=\frac{3}{4}$,
∵AE = AO - EO = 1,
∴$\frac{1}{AF}=\frac{3}{4}$,
∴AF = $\frac{4}{3}$.
∴FO = 3 - $\frac{4}{3}=\frac{5}{3}$.
∵$\frac{BE}{B'F}=\frac{3}{B'F}=\frac{3}{4}$,
∴B'F = 4,
∴点B'的坐标为($\frac{5}{3}$, -4).

10.[几何直观]阅读与思考:利用图形计算器或计算机等信息技术工具,可以很方便地将图形放大或缩小,还可以探索位似的性质.
小明利用几何画板软件,尝试用“观察—猜想—验证—应用”的方法进行探究,步骤如下:如图1,任意画一个△ABC,以点O为位似中心,设置新、旧图形的相似比为k,得到△A'B'C'.

第一步:测量对应边的长度,并计算它们的比值,发现结果与k的值相等.
第二步:以O为原点建立平面直角坐标系,分别写出点A,A'的横坐标,并计算比值;分别写出点A,A'的纵坐标,并计算比值.观察比值与k的关系,发现它们相等.接下来对其他顶点进行相同的操作,得出相同的结论.
第三步:作线段OA,OA',OB,OB',OC,OC',测量各线段的长度,将发现的结论用文字总结出来.
第四步:任意改变△ABC的位置,并按相同步骤作图及探究,发现上面探究得出的结论仍然成立.
于是,小明总结并得出了位似的性质.
(1)第三步发现的结论是______________________________;
(2)若图1中A(6,2),A'(9,3),B(4,3),S△ABC = 2,则点B'的坐标是______,S△A'B'C' = ______;
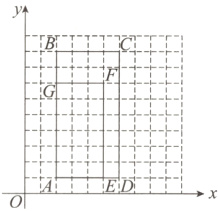
(3)如图2,以点A为位似中心,在给定的网格中画出与矩形ABCD的相似比为0.75的矩形.

小明利用几何画板软件,尝试用“观察—猜想—验证—应用”的方法进行探究,步骤如下:如图1,任意画一个△ABC,以点O为位似中心,设置新、旧图形的相似比为k,得到△A'B'C'.

第一步:测量对应边的长度,并计算它们的比值,发现结果与k的值相等.
第二步:以O为原点建立平面直角坐标系,分别写出点A,A'的横坐标,并计算比值;分别写出点A,A'的纵坐标,并计算比值.观察比值与k的关系,发现它们相等.接下来对其他顶点进行相同的操作,得出相同的结论.
第三步:作线段OA,OA',OB,OB',OC,OC',测量各线段的长度,将发现的结论用文字总结出来.
第四步:任意改变△ABC的位置,并按相同步骤作图及探究,发现上面探究得出的结论仍然成立.
于是,小明总结并得出了位似的性质.
(1)第三步发现的结论是______________________________;
(2)若图1中A(6,2),A'(9,3),B(4,3),S△ABC = 2,则点B'的坐标是______,S△A'B'C' = ______;
(3)如图2,以点A为位似中心,在给定的网格中画出与矩形ABCD的相似比为0.75的矩形.

答案:
解:
(1) 位似中心与对应点连线长度之比等于相似比.
(2) (6, 4.5); 4.5.
(3) 如图, 矩形AEFG即为所求.

解:
(1) 位似中心与对应点连线长度之比等于相似比.
(2) (6, 4.5); 4.5.
(3) 如图, 矩形AEFG即为所求.


查看更多完整答案,请扫码查看


